⤨ PCA ③ 벡터의 기하학: 벡터와 좌표

Lightman·2021년 8월 1일

벡터 변환 좌표

MACHINE LEARNING 🦾

목록 보기

3/9

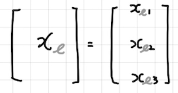
벡터의 기하학적 해석: 점과 좌표

벡터는 좌표계에 표현되는 하나의 점, 또는 화살표로 해석된다. 그렇다면 좌표란 무엇일까?

좌표

[정의] 좌표란 기저벡터를 선형조합하여 그 벡터w를 나타내기 위한 계수벡터이다.

표준기저벡터의 경우: 좌표 $x_e$ 는 선형조합의 결과와 같다.
표준기저벡터가 아닌 경우: 좌표 $x_g$ 는 선형조합의 결과와는 다르다.

[해석] 따라서 좌표는 기저벡터에 대한 상대적인 위치이고, 선형조합의 결과는 기저벡터e를 기준으로 한 절대적인 위치라고 생각할 수 있다.

변환: 점 변환과 좌표 변환

변환에 대하여 두 가지 관점을 생각해볼 수 있다. 하나는 점 변환으로, 기존의 기저벡터를 새로운 기저벡터로 변환할 때 기존의 점 $x$ 는 어떤 점으로 이동하는지를 나타내는 것이다. 이 방법은 보다 직관적이다. 또 다른 하나는 좌표 변환으로, 임의의 좌표 $x$ (또는 $x_e$ )를 새로운 기저벡터 위의 좌표 $x_g$ 로 나타내는 것이다. 이 방법은 보다 수학적이다.

🚩목표1 점 변환: 새로운 기저벡터로 변환할 때 기존의 점 x는 기존의 기저벡터에서 어떤 점x'으로 이동하는지 나타내기[점 변환행렬: $A$ ]

[목표] 표준기저벡터의 선형조합으로 표현된 점 $x$ 를 새로운 기저벡터의 선형조합으로 표현하면 점 $x'$ 는 표준기저벡터에서 어떤 점이 될까 ?

이 부분은 직관적이다.

이때, 점 $x$ 의 좌표 $x_e$ 는 표준기저벡터 $e_1, e_2$ 의 계수를 담고 있다.

이 계수를 $e_1, e_2$ 가 아닌 $g_1, g_2$ 에 곱해줌으로써 $g_1, g_2$ 를 기저벡터로 하는 평면에서 이 점을 추적할 수 있다.

[해석] 이 관점에서 행렬과 벡터의 곱 $Aw$ 를 두 기저벡터와 한 점 사이의 선형조합으로 보는 시각을 얻을 수 있다!

🚩목표2 좌표 변환: 임의의 좌표 $x_e$ 를 새로운 기저벡터의 좌표 $x_g$ 로 나타내기[좌표 변환행렬: $A^{-1}$ ]

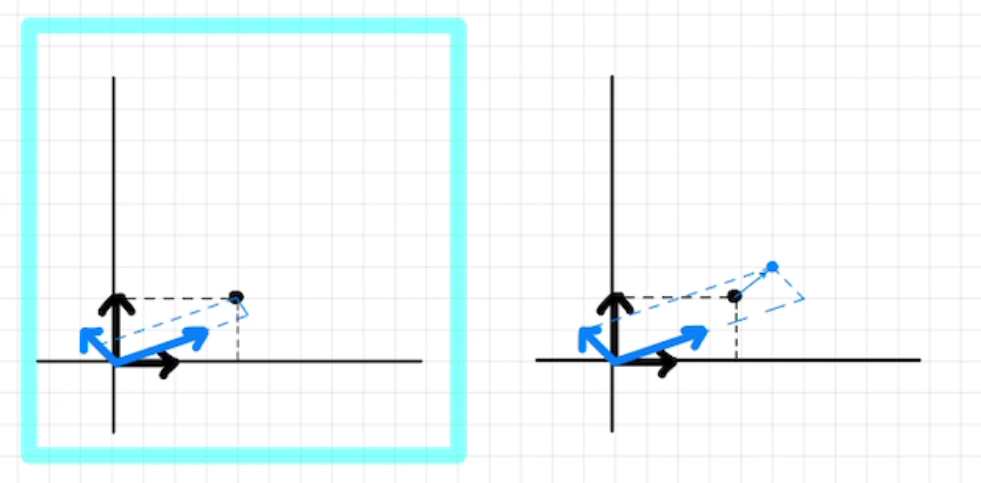
[목표] 표준기저벡터에서 표현된 좌표 $x_e$ 로 부터 새로운 기저벡터에서 표현된 좌표 $x_g$ 를 어떻게 도출할 것인가?

이 부분은 보다 tricky하다.

이때, 기저벡터를 $e → g$ 로 옮기는 변환을 적용하여 점 $x$ 가 되는 점 $y$ 를 상상하자.

점 $y$ 는 $Ay = x$ 를 만족한다. 이때, 좌표 $y_e$ 와 좌표 $x_g$ 의 상대적인 위치가 같다.

따라서 점 $y$ 의 좌표 $y_e$ 가 점 $x$ 의 기저벡터 $g$ 상의 좌표 $x_g$ 가 된다.

① 표준기저벡터로 부터 새로운 기저벡터를 얻어내기

새로운 기저벡터는 하나의 벡터이므로 표준기저벡터의 점 변환으로 획득할 수 있다.

② 좌표변환 행렬

①식과 x의 절대적인 위치는 일정하다는 사실을 이용해 다음과 같이 좌표변환 행렬 ${A^{-1}}$ 을 얻을 수 있다.

그렇다면 다음과 같은 관계가 성립한다. 이것이 내포한 의미는 무엇일까 ?

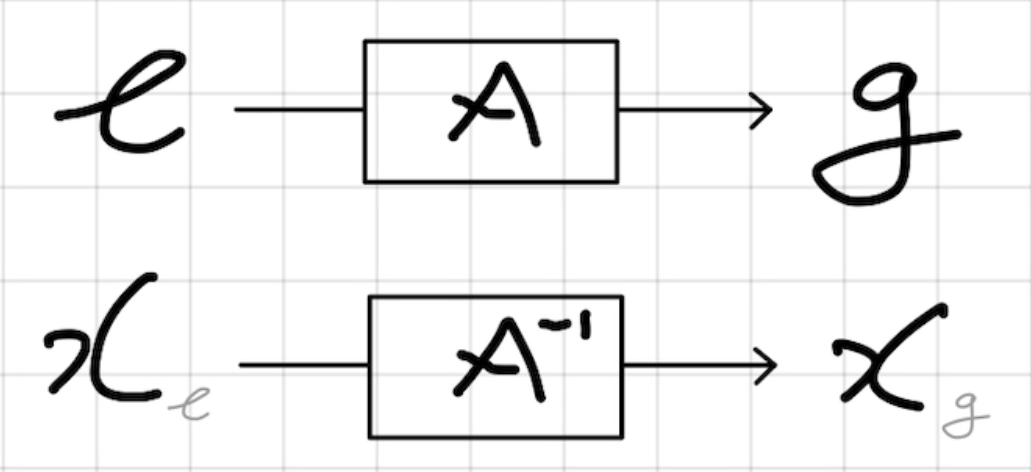
[해석] 좌표변환하여 $Ay = x$ 가 되는 새로운 점 $y$ 를 상상하자. 그럼 $x = A^{-1}y$ 가 성립한다. 이 관점에서 좌표 $x_g$ 를 찾는 문제는 기존의 기저벡터에서 점 $x$ 로 변환될 점 $y$ 를 찾는 문제로 치환된다. 즉, 점 $y$ 는 $A$ 변환하여 새로운 기저벡터 상의 좌표 $x_g$ 가 가리키는 점 $x$ 가 되고 $y$ 의 좌표 $y_e$ 는 점 $y$ 인 동시에 좌표 $x_g$ 이다.

끝.

참고자료

Lightman

현직 데이터 분석가 / 데이터 과학의 정도를 따라 🚲 / About DEV DA ML

⤨ PCA ③ 벡터의 기하학: 벡터와 좌표

MACHINE LEARNING 🦾

벡터의 기하학적 해석: 점과 좌표

좌표

변환: 점 변환과 좌표 변환

🚩목표1 점 변환: 새로운 기저벡터로 변환할 때 기존의 점 x는 기존의 기저벡터에서 어떤 점x'으로 이동하는지 나타내기[점 변환행렬: $A$ ]

🚩목표2 좌표 변환: 임의의 좌표 $x_e$ 를 새로운 기저벡터의 좌표 $x_g$ 로 나타내기[좌표 변환행렬: $A^{-1}$ ]

① 표준기저벡터로 부터 새로운 기저벡터를 얻어내기

② 좌표변환 행렬

끝.

참고자료

⤨ PCA ② 벡터의 기하학: 벡터공간과 기저벡터

⤨ PCA ④ 벡터의 선형독립과 행렬의 RANK

0개의 댓글

⤨ PCA ③ 벡터의 기하학: 벡터와 좌표

MACHINE LEARNING 🦾

벡터의 기하학적 해석: 점과 좌표

좌표

변환: 점 변환과 좌표 변환

🚩목표1 점 변환: 새로운 기저벡터로 변환할 때 기존의 점 x는 기존의 기저벡터에서 어떤 점x'으로 이동하는지 나타내기[점 변환행렬: AAA]

🚩목표2 좌표 변환: 임의의 좌표 xex_exe​를 새로운 기저벡터의 좌표xgx_gxg​로 나타내기[좌표 변환행렬: A−1A^{-1}A−1]

① 표준기저벡터로 부터 새로운 기저벡터를 얻어내기

② 좌표변환 행렬

끝.

참고자료

⤨ PCA ② 벡터의 기하학: 벡터공간과 기저벡터

⤨ PCA ④ 벡터의 선형독립과 행렬의 RANK

0개의 댓글

🚩목표1 점 변환: 새로운 기저벡터로 변환할 때 기존의 점 x는 기존의 기저벡터에서 어떤 점x'으로 이동하는지 나타내기[점 변환행렬: $A$ ]

🚩목표2 좌표 변환: 임의의 좌표 $x_e$ 를 새로운 기저벡터의 좌표 $x_g$ 로 나타내기[좌표 변환행렬: $A^{-1}$ ]