벡터공간VectorSpace

[정의] 벡터공간이란 선형독립인 N개의 벡터가 선형조합으로 만들어 내는Span 공간을 의미한다.

$V = \{ c_1x_1 + ... + c_Nx_N | c_1, ... , c_N ∈ R \}$

• 이때, 선형독립인 N개의 벡터 ${ x_1, ... ,x_N}$를 기저벡터basis라고 하고,
• 기저벡터basis의 개수 N을 차원dimension이라고 한다.

벡터공간의 정리: N차원 공간의 형성

[정리] N개의 N차원 벡터 ${ x_1, ... ,x_N}$가 선형독립일 때, 다음 두 정리를 만족한다.

• 해당 벡터를 선형조합하여 모든 N차원 벡터를 만들 수 있다.
• 해당 벡터에 모두 수직인 영벡터가 아닌 벡터x는 존재하지 않는다.

벡터공간의 투영

[정의] N차원 기저벡터 M개 ${ v_1, ... ,v_M}$가 있을 때, 이 기저벡터의 선형조합으로 나타나는 $x^{||V}$에 대해, $(x - x^{||V}) ⊥ \{v1, v2, ... ,vM\}$ 가 성립하면 $x^{||V}$는 투영벡터, $x^{⊥V}$는 직교벡터가 된다.

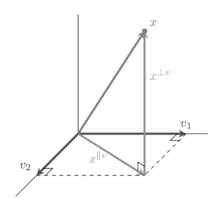
그러나 일반적인 경우 $x^{||V}$을 구하는 일은 쉽지 않고, 기저벡터가 정규직교orthonormal인 경우는 쉽게 표현할 수 있으며 유용하다.

[정리]
N차원 기저벡터 M개 ${ v_1, ... ,v_M}$가 정규직교orthonormal할 때, $let~x^{||V} = \sum(x\cdot v_i)v_i$이면 $x^{||V}$는 투영벡터, $x^{⊥V} = x - x^{||V}$는 직교벡터가 된다. 또한 피타고라스 정리에 의해 ${||x^{||V}||}^2 = \sum(x\cdot v_i)^2$이 된다.

• [lemma] 직교벡터$x^{⊥V}$는 기저벡터${ v_1, ... ,v_M}$로 이루어진 벡터공간의 모든 벡터에 대해 직교한다.
• [lemma] 벡터x의 투영벡터$x^{||V}$는 기저벡터${ v_1, ... ,v_M}$로 이루어진 벡터공간의 모든 벡터 중에서 가장 벡터 x와 거리${||x^{||V}||}$가 가까운 벡터이다.