" 여기까지 잘 따라와 주셔서 감사합니다! "
우리는 지금까지 자료구조가 무엇인지, 왜 해야하는지, 자료구조와 알고리즘은 어떤 관계인지를 살펴보았다. 그리고 가장 익숙한 자료구조인 배열에 대해 알아보았고, 배열이 항상 효율적인 것은 아니라는 사실을 알게 되었다. 그리고 그런 배열의 단점
- 비효율적인 삽입과 삭제
를 해결하기 위해 연결 리스트를 사용할 수 있음을 알게 되었다.
이제 본격적으로 연결 리스트가 "어떻게" 그 비효율을 해결할 수 있는지 알아볼 시간이다.
연결 리스트는 초반에는 낯설게 다가올 수 있지만, 나중에 가서는 오히려 배열을 사용하는 것이 더 어색해질 정도로 잘 다룰 수 있게 된다. 특히 트리를 공부할 때 연결 리스트는 몰라서는 안 되는 개념이 된다. 물론 거기까지 잘 따라온다면 여러분은 이미 연결 리스트 마스터가 되어 있을 것이니 걱정할 필요 없다.
처음에는 다 어렵다. 그것을 받아들이고 이해가 되지 않더라도 자책하지 말고 댓글로 질문을 올려주거나 GPT에게 물어보거나 검색을 많이 해보기를 바란다. 필자 또한 그렇게 익혀야 했다.
자, 숨 한 번 고르고 다시 시작해 보자.
연결 리스트란?
말 그대로다. 자료들이 리스트 형태로 되어 있는데 그들끼리 연결되어 있는 것이다. 배열의 경우 연결하고 있다고 말하기에는 애매한 부분이 있었다. 직전에 배운 귀여운 int형 size 3의 배열을 다시 한 번 보자.
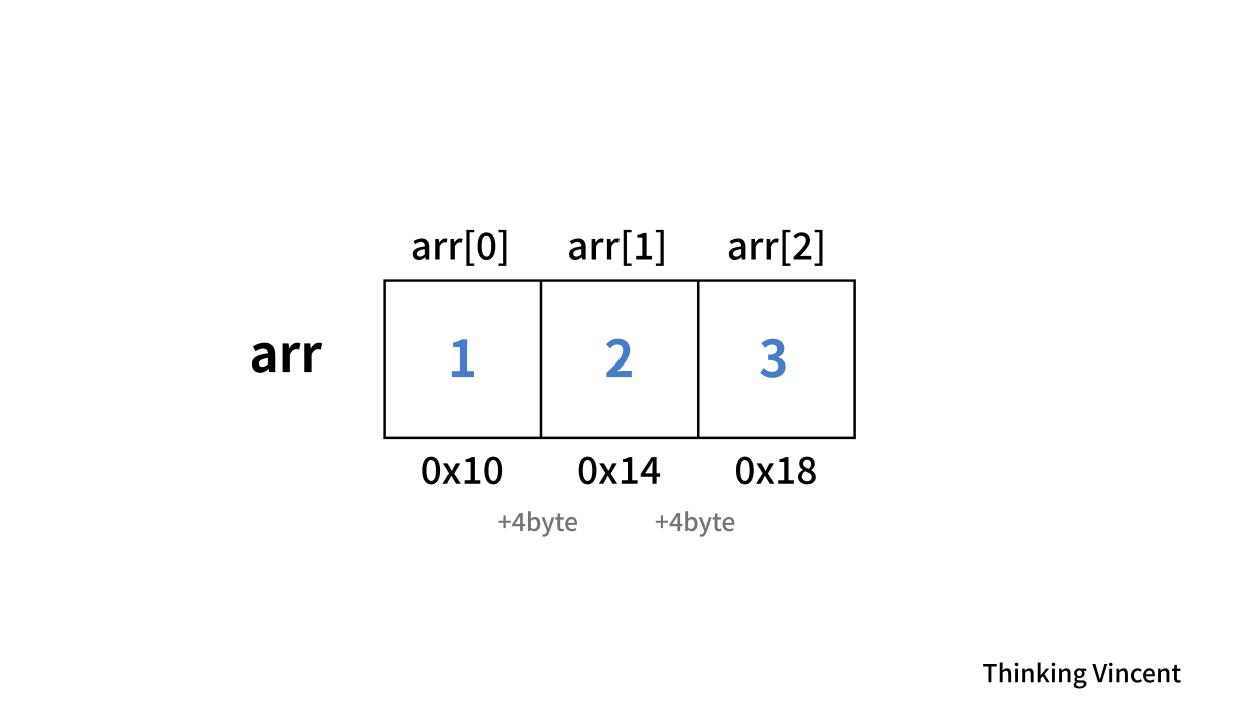
이들은 눈으로 보아서는 얼핏 연결된 것 처럼 보이지만 사실 배열 자체가 연결을 상징하지는 않는다. 현재 배열의 각 요소들은 4byte를 기준으로 연속된 메모리 공간에 선형적으로 들어가 있는 것이지 arr[0]과 arr[1]이 서로 연결되어있다~ 라고 보기에는 아쉬운 감이 있다. 그냥 옆에 서 있기만 하고 손을 잡지는 못 한 관계 정도로 이해하면 좋을 것 같다.
그러나 연결 리스트는 확실하게 연결되어 있다.
그림으로 나타낸 가장 심플한 연결 리스트 그림을 한 번 보자.
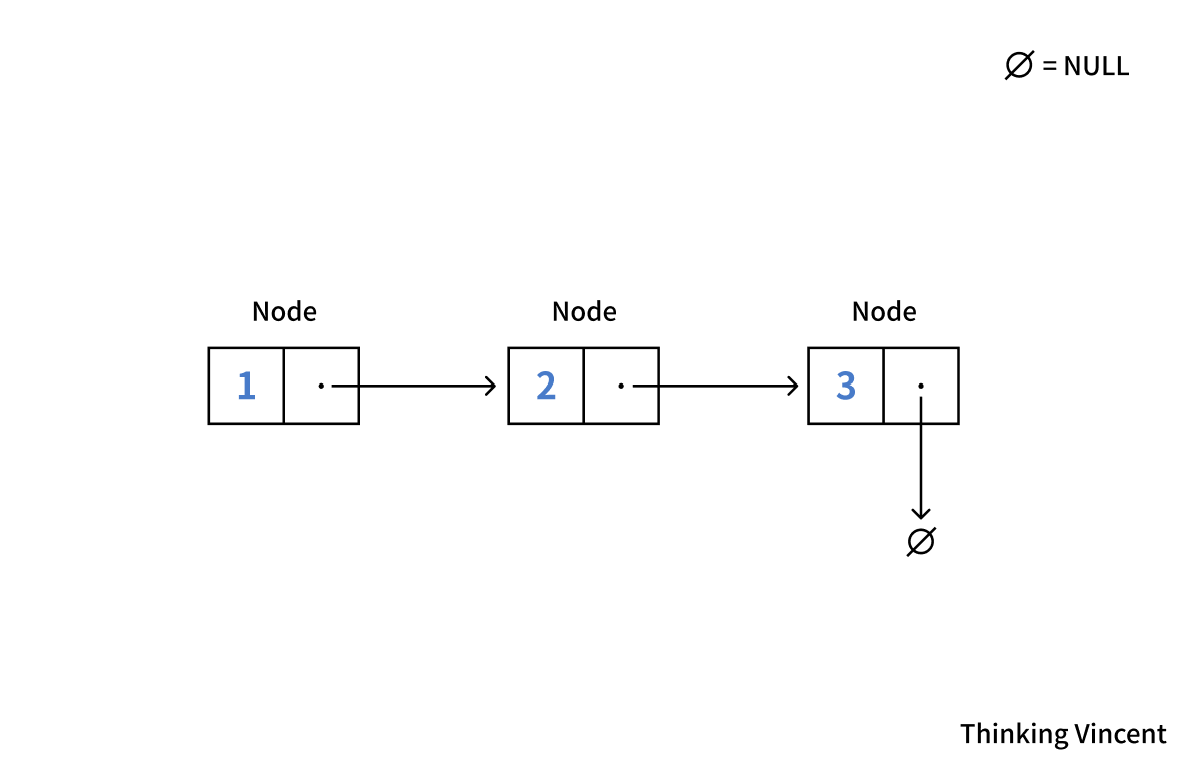
어떤가, 저 화살표가 보이는가? 저 화살표 덕분에 자료를 가지고 있는 노드(Node)라 불리는 것들이 서로 "연결(Link)"되게 된다. 배열이랑은 확실히 형태가 달라 보인다. 그리고 각 Node들은 배열과 달리 아무 주소에나 저장될 수 있다. 귀여운 3개짜리 int형 배열처럼 4byte마다 하나씩 연속적으로 저장될 필요가 없다는 것이다.
자, 연결 리스트를 확실하게 이해하기 위해 내부 구조를 함께 하나씩 뜯어 보자.
연결 리스트의 구조
노드 (Node)
노드는 매듭, 집합점, 중심점 등 다양한 의미로 해석된다. 여기서는 그냥 자료를 저장하는 곳으로 이해하면 되겠다. 일종의 기차 칸이랄까?
서부시대 철도 위에 금과 석탄과 소금을 실은 기차가 있다면 그 각각의 기차 칸들이 노드인 것이다.
기차 칸과 기차 칸이 연결되어 기차가 되듯 노드와 노드가 연결되어 연결 리스트가 된다.

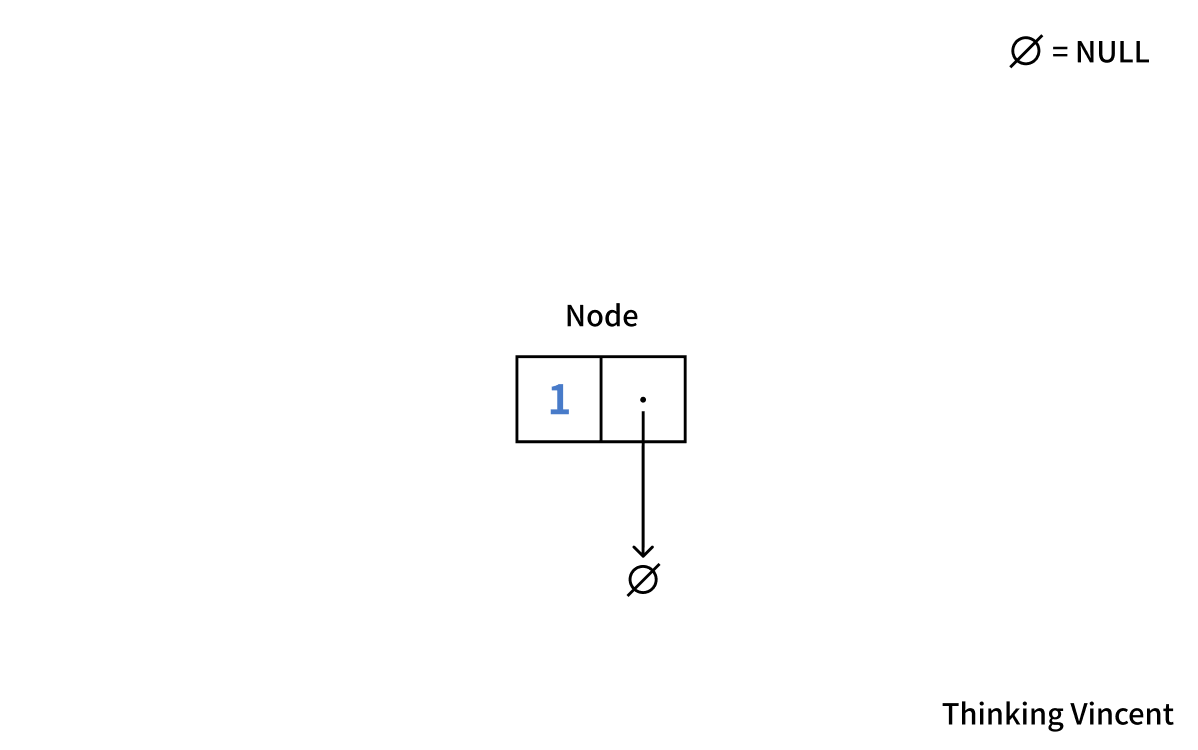
노드는 그림을 그려보면 이렇게 생겼다.
어떤가? 생각보다 귀엽지 않은가? 사실 이게 연결 리스트의 시작이자 끝이다!
잘 보면 노드는 반으로 나뉘어져 있는 것 같다. 왼쪽에는 1이라는 자료가 들어있고 오른쪽에는 영문 모를 점이 하나 보인다.
그리고 그 점에서 튀어나온 화살표 하나가 NULL을 가리키고 있다.
왼쪽은 당신의 자료가 들어갈 공간이고, 오른쪽은 이 노드가 다른 노드로 연결될 수 있도록 도와주는 포인터 변수가 들어갈 공간이다.
포인터라는게 그렇지 않는가. 다른 무언가를 가리킬 수 있는 변수. 가리키는 모습을 화살표로 표현하면 이해가 쉽다.
다시 정리하면, 저 점으로 나타난 포인터 변수가 연결된 기차 칸(노드)을 가리키게 되는 것이다. 정확히는 주소를 저장한다.
자, 노드를 class로 한 번 정의해보자. 좀 더 와 닿을지도 모른다.
class Node { //멤버함수 없이 사용할 것이라면 struct로 해줘도 된다.
private:
int data = 0; // 저장할 자료. 타입은 정하기 나름.
Node* next = NULL;
// 다음 노드를 가리킬 포인터 변수. nullptr로 초기화해도 무관.
friend class LinkedList;
// LinkedList 클래스에서 Node 클래스의 private 변수들에 접근하기 위함.
}이게 가장 기본적인 노드의 형태이다. int 타입의 자료와 next라는 포인터 변수 하나를 가지고 있다. 이게 전부다.
처음에는 아무것도 연결하지 않았기 때문에 next를 NULL로 초기화 해준 것이다. data 또한 0(없음)으로 초기화했다.
그러나 이 노드만을 가지고는 아무것도 할 수 없다. 기차 칸만 따로 따로 가지고 있는 것이다. 실제로 기차를 만들어 끌고 다니기 위해서는 기차들을 연결하는 과정이 필요하다.
따라서 Node를 연결하고 관리하기 위한 LinkedList class를 하나 만들어 줘야 한다.
LinkedList 클래스에서 Node 클래스의 private 변수들을 사용하기 위해 Node 클래스에서 LinkedList 클래스를 friend로 지정한 것이다.
바로 LinkedList class를 살펴보자.
연결 리스트 (Linked List)
class LinkedList {
private:
Node* head; // 맨 앞 노드를 가리키는 포인터 변수
Node* tail; // 맨 뒤 노드를 가리키는 포인터 변수
int listSize; // 저장된 노드의 수를 저장하는 변수
public:
LinkedList() { // NULL, 0으로 초기화
head = NULL;
tail = NULL;
listSize = 0;
}
bool empty() { // 리스트가 비어있으면 true를 리턴
return listSize == 0;
}
void insert(int idx, int data) { // idx(0 ~ ) 위치에 data가 저장된 새 노드를 삽입
...
}
void deletion(int idx) { // idx(0 ~ ) 위치에 있는 노드를 삭제
...
}
void print() { // 리스트에 저장된 노드를 head부터 tail까지 출력
...
}이렇게 하면 연결 리스트를 구현하기 위한 기본적인 재료들이 다 모였다.
연결 리스트의 특징과 기능
head와 tail
바로 위 코드에서 변수 목록을 살펴보자. listSize는 저장된 노드 수를 확인하기 위한 변수이다. 그런데 head와 tail이라는 특이한 포인터 변수가 보인다.
head는 머리다. 리스트의 가장 앞 노드를 가리킬 것이다. tail은 꼬리다. 리스트의 가장 마지막 노드를 가리킬 것이다. 기차로 치면 가장 앞 칸과 가장 뒷 칸을 가리키는 변수들인 것이다.
그럼 왜 이런 특이한 변수들이 필요할까?
head를 활용한 접근
그림을 보자.
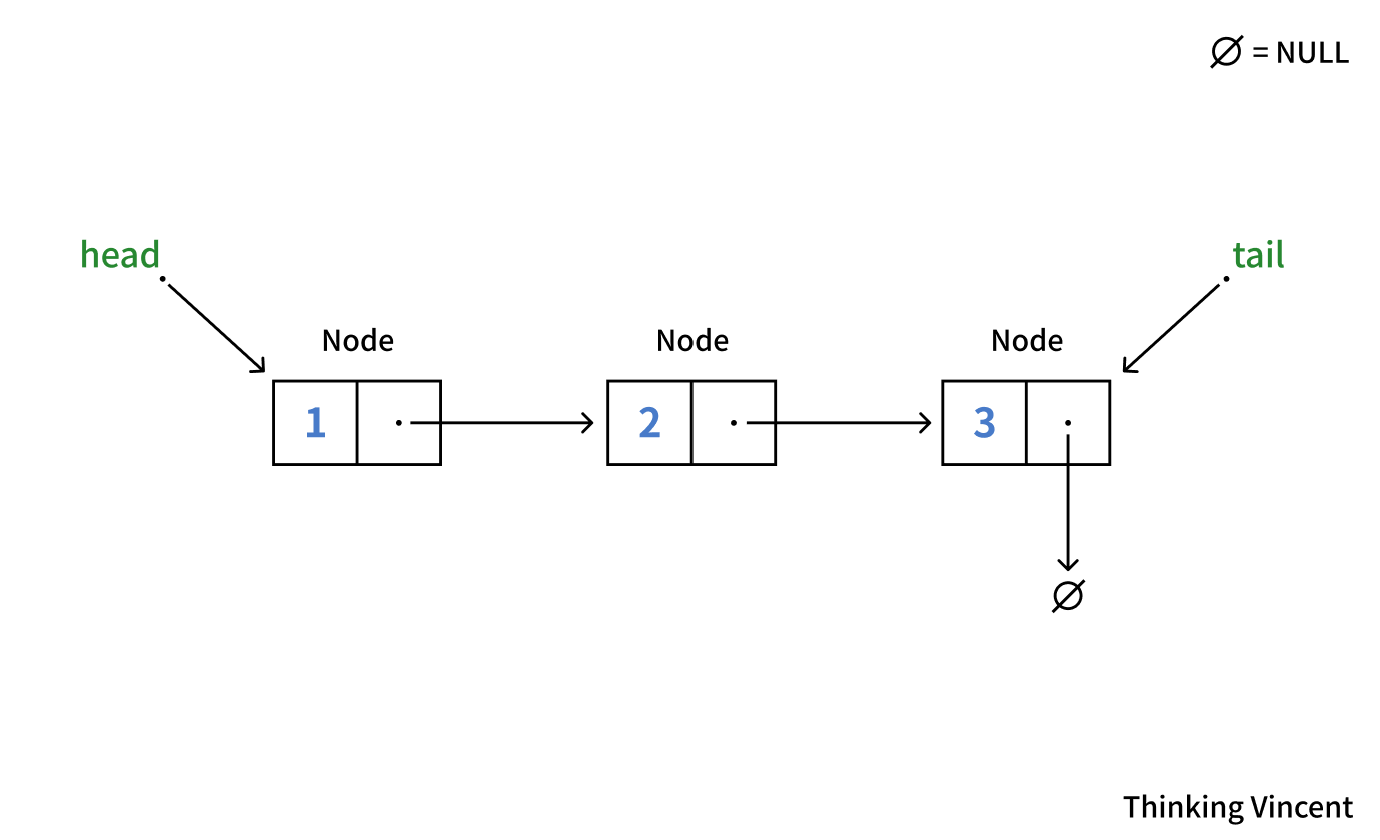
만약 우리가 2가 자료로 저장된 노드에 접근하길 원한다면 어떻게 해야할까?
배열이었다면 arr[index]로 한 번에 접근이 가능했겠지만, 연결 리스트는 그렇지 않다. 연결 리스트의 각 노드들은 배열처럼 연속된 메모리가 아닌 임의의 메모리에 따로 따로 저장되어 있기 때문에 한 번에 접근이 불가능하다. 따라서 가장 앞과 뒤를 가리키는 head와 tail 포인터 변수를 만들고, 이것을 통해 중간에 있는 노드들에 접근하는 것이다.
만약 우리가 2에 접근하여 출력하길 원한다면
cout << head->next->data;이런식으로 우선 head로 첫 번째 노드를 참조한 뒤, 그 노드의 next 포인터 변수를 통해 다음 노드를 참조하고, 그렇게 참조된 노드의 data를 출력해야 하는 것이다.
"그럼 반대로 tail에서 앞으로 참조할 수는 없나요?"
아직은 불가능하다. 화살표 방향을 보면 모든 노드는 자신의 뒤에 오는 노드에 대한 정보만 가지고 있다. 따라서 뒤에서 앞으로 접근하는 것은 불가능하다. 이런 단방향 연결 리스트 구조를
"단일 연결 리스트 (Singly Linked List)"라고 부른다.
비유하자면 입구가 제일 앞 칸에만 있고, 꼬리칸을 향해서만 이동이 가능한 이상한 기차인 것이다. (설국열차...?)
따라서 우리가 특정 data가 들어있는 노드를 탐색하길 원한다면
항상 head에서부터 해당 data가 들어있는 노드를 만날 때 까지 next 변수를 통해 접근해야 한다.
만약 노드가 여러개라면, 우리는 head->next->next->next...와 같은 방식으로 접근하거나
Node* cursor = head;
while (cursor != NULL) {
// cursor가 tail의 next(NULL)일 때 까지 반복하며 모든 노드를 확인한다.
cursor = corsor->next;
}이런식으로 반복문을 통해 지속적으로 현재 참조하고 있는 노드를 업데이트 해야 한다.
따라서 연결 리스트는 특정 노드의 주소를 모르는 상태로 접근하거나 탐색할 때 더 많은 시간이 걸린다. 앞에서부터 하나 하나 찾아야 하니까!
삽입과 삭제
삽입
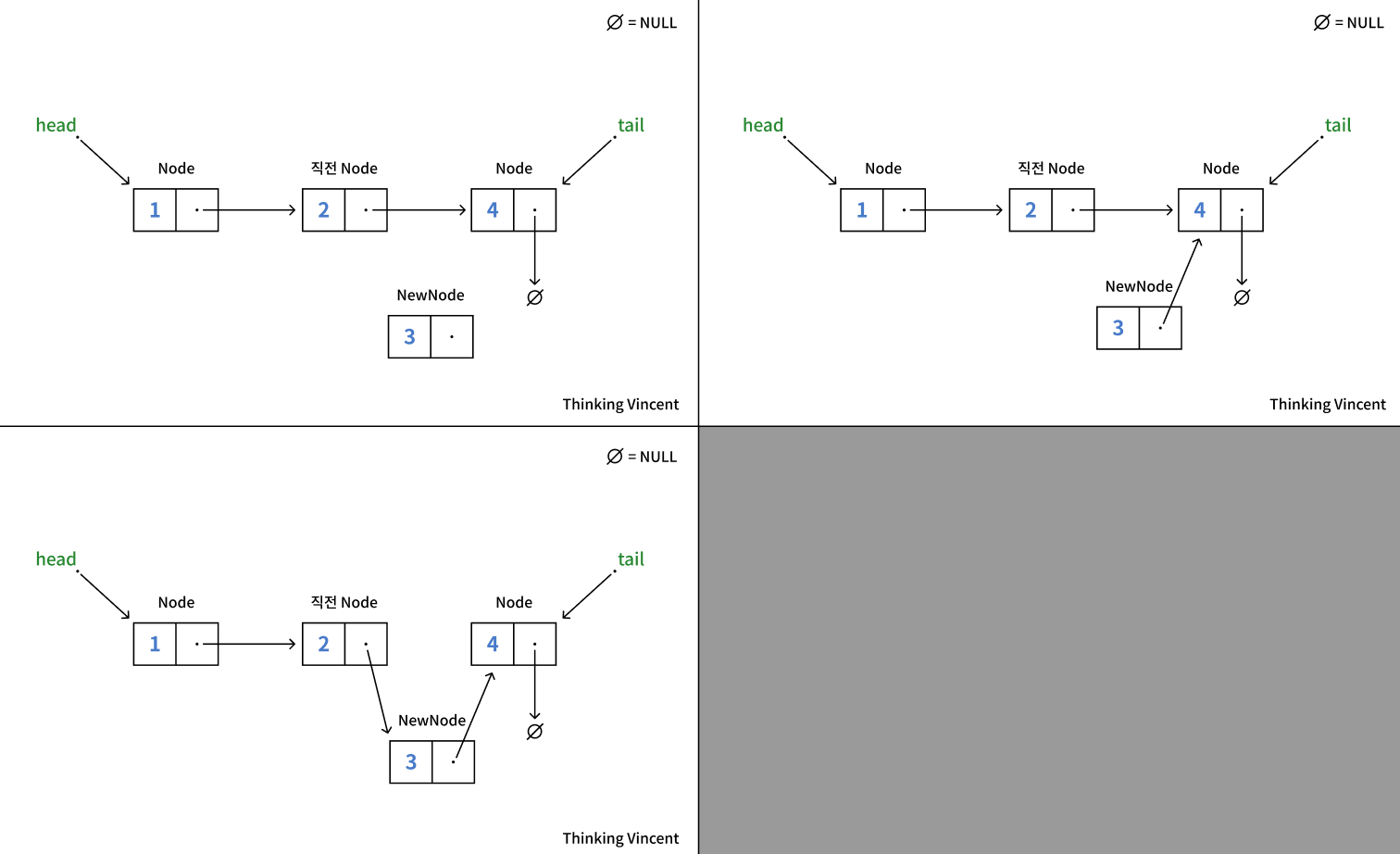
연결 리스트의 삽입은 다음과 같은 순서로 이루어진다.
- 새로운 노드를 동적으로 생성
- 삽입할 위치의 직전 노드를 탐색
- 새 노드의 next를 직전 노드의 next로 연결
- 직전 노드의 next를 새 노드로 연결
그림으로는 이렇게 된다.
삽입 시 주의할 점
만약 삽입할 위치가 처음이나 끝이라면 head와 tail을 새로운 노드로 반드시 새롭게 업데이트 해주어야 한다.
또한 아무것도 없는 상태에서 head와 tail은 모두 NULL이기 때문에, 첫 번째로 노드가 추가되면 head와 tail가 모두 해당 노드를 가리키게 해야한다.
삭제
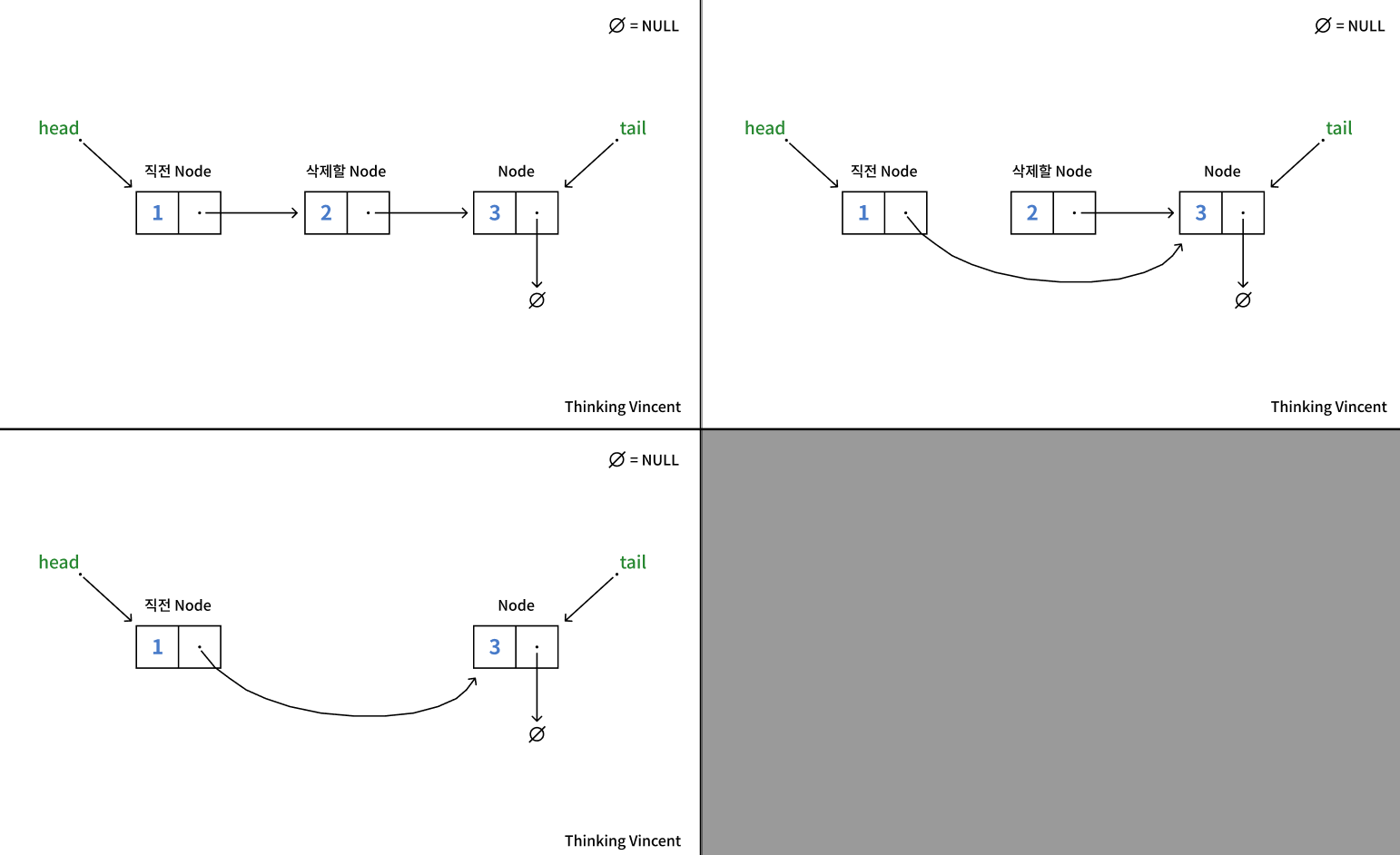
삭제의 경우 다음과 같은 순서를 거친다.
- head에서부터 삭제할 노드와 삭제할 노드의 직전 노드를 찾는다.
- 직전 노드의 next를 삭제할 노드의 next로 업데이트한다.
- 삭제할 노드를 delete한다.
그림으로는 다음과 같다.
삭제 시 주의할 점
여기서도 반드시 고려해야 할 점이 있다.
노드가 하나 뿐이라면 head와 tail은 모두 그 노드를 가리키고 있을 것이다.
따라서 이 경우, 해당 노드를 삭제하고 나면 반드시 head와 tail을 NULL로 업데이트 해야한다. 그렇지 않으면 head와 tail은 삭제된 공간을 참조하게 되어 예측하지 못 한 결과를 낳을 수 있다.
또한 삭제할 노드가 head였을 경우, tail이었을 경우를 고려하여 각각 새롭게 업데이트를 해줘야한다.
배열과 연결 리스트 비교
이제 배열과 연결 리스트의 장단점을 비교해보자.
배열
장점
- 인덱스를 통한 빠른 접근
단점
- 사이즈에 제약을 받음
- 삽입 시 Shift 처리
- 삭제 시 Shift 처리
연결 리스트
장점
- 사이즈에 제약이 없음
배열과 달리 필요에 따라 노드를 생성하고 연결해주는 방식이기 때문에 사이즈에 제약을 받지 않는다. - 간편한 삽입
일단 삽입할 위치에 대한 탐색을 완료하고 나면 그냥 새롭게 연결관계만 만들어주면 끝난다. Shift 처리가 불필요하다. - 간편한 삭제
일단 삭제할 위치에 대한 탐색을 완료하고 나면 삽입처럼 새롭게 연결관계를 만들어주면 끝난다. Shift 처리가 불필요하다.
단점
- 접근이 비교적 오래 걸림
인덱스로 바로 참조할 수 없고, head를 통해서만 접근이 가능하기 때문에 첫 접근이 배열에 비해 오래 걸린다.
결론
index가 주어졌을 경우의 탐색과 접근 연산이 많다면 배열을 사용하고, 삭제와 삽입 연산이 많다면 연결 리스트를 사용하는 것이 유리하다.
또한 사이즈가 유동적으로 바뀌어야 할 경우 연결 리스트를 사용하는 것이 유리하다.
이렇듯 배열과 연결 리스트는 서로의 장단점을 보완해준다. 따라서 목적에 따라 다르게 사용해줄 수 있고 어느 하나가 절대적으로 뛰어나다고 말할 수 없다.
다만, 연결 리스트의 상대적으로 느린 접근 시간을 조금 더 빨리 만들어 줄 수 있는 방법이 존재한다.
바로 "이중 연결 리스트 (Doubly Linked List)"이다.
이중 연결 리스트를 사용하여 우리는 head가 아닌 tail로부터의 접근을 시도할 수 있다. 이것은 다음 챕터에서 알아보도록 하자.
실습을 위한 코드
#include <iostream>
using namespace std;
class Node {
private:
int data = 0;
Node* next = NULL;
friend class NodeList;
};
class NodeList {
private:
int listSize;
Node* head;
Node* tail;
public:
NodeList() {
listSize = 0; head = tail = NULL;
}
bool empty() {
return listSize == 0;
}
void append(int data) { //제일 뒤에 추가
Node* newNode = new Node;
newNode->data = data;
if (empty()) {
head = tail = newNode;
++listSize;
return;
}
tail->next = newNode;
tail = newNode;
++listSize;
}
void insertion(int idx, int data) {
if (idx < 0 || idx > listSize) {
return;
}
else if (idx == listSize) { //제일 뒤에 추가 또는 빈 리스트에 추가
append(data);
}
else if (idx == 0) { //제일 앞에 추가
Node* newNode = new Node;
newNode->data = data;
newNode->next = head;
head = newNode;
++listSize;
}
else { //중간에 추가
Node* newNode = new Node;
newNode->data = data;
Node* preNode = head;
for (int i = 1; i < idx; ++i) {
preNode = preNode->next;
}
newNode->next = preNode->next;
preNode->next = newNode;
++listSize;
}
}
void deletion(int idx) { //삭제
if (idx < 0 || idx >= listSize || empty()) {
return;
}
Node* cursor = head;
if (idx == 0) { //첫 번째 원소를 삭제
if (listSize == 1) { //하나뿐일때
head = tail = nullptr;
}
else {
head = head->next;
}
}
else {
Node* pre = head;
for (int i = 0; i < idx; ++i) {
pre = cursor;
cursor = cursor->next;
}
pre->next = cursor->next;
if (cursor == tail) {
tail = pre;
//pre->next = nullptr; 위에서 이미 함.
}
}
delete cursor;
--listSize;
}
void print() {
if (empty()) {
cout << "empty!\n";
return;
}
Node* cursor = head;
for (int i = 0; i < listSize; ++i) {
cout << cursor->data << ' ';
cursor = cursor->next;
}
cout << '\n';
}
};
int main() {
NodeList myNode;
string str;
int data = 0, index = 0;
cin >> str;
while (cin) {
if (str == "append") {
cin >> data;
myNode.append(data);
}
else if (str == "insert") {
cin >> index >> data;
myNode.insertion(index, data);
}
else if (str == "delete") {
cin >> index;
myNode.deletion(index);
}
else if (str == "print") {
myNode.print();
}
cin >> str;
}
}