[자료구조 A to Z] 배열의 치명적인 문제점

" 본 챕터는 연결 리스트로 넘어가기 위한 필수 과정이다. "

아 연결 리스트 왜 하는건데?

처음 연결 리스트를 구현하는 초심자들은 적잖이 당황할 것이다. 실제로 필자는 작년 이맘때 쯤 객체지향 프로그래밍 1 수업의 막바지에서 처음으로 단일 연결 리스트를 구현하게 되었다. 그리고 그게 컴공 입문에 있어서 재귀 함수에 이은 두 번째 난관이었다.

세상에, 안그래도 어려운 포인터 변수를 이렇게 많이 사용한다고? 도대체 이런게 왜 필요한건데? 그냥 배열 쓰면 되잖아!!!!

아마 많은 사람들이 이렇게 생각할 것이고, 이렇게 생각했을 것이다(나).
그러나, 연결 리스트의 장점을 자료구조에서 배우게 되면 비로소 그 가치를 알게 된다. 무한 등비 급수의 합 공식도 틀려먹던 나도 했으니 당신도 할 수 있다.

먼저 연결 리스트가 등장한 배경에 대해 알아보도록 하자. 그 배경은 배열의 특징과 관련이 있다. 알고 나면 배열이 아주 나쁜 아이로 보일지도 모른다!

그리고... 비밀 아닌 비밀을 말하자면, 연결 리스트를 모르면 뒤에 나올 자료구조 대부분을 이해하지 못 할 것이다!!!!!!!!

그렇다고 지레 겁먹지는 마라. 처음에는 다 어렵다. 자료구조를 하기로 마음을 먹었다면 포기하지 않는 것이 가장 중요하다. 나도 했으니 당신도 할 수 있다.

배열의 특징

자, 저번 시간에 배열에 대해 설명했었다. 그러나 배열에 새로운 요소를 추가하거나 삭제하거나, 탐색하는 기능에 대해서는 자세히 언급하지 않았다.
지금 한 번 간단하게 알아보자.

배열에서의 요소 접근 (access)과 변경 (change)

배열에서 요소 접근은 가히 치트키라 부를 수 있을 만큼 쉽다.
가정해보자. 우리에게 전과 같이

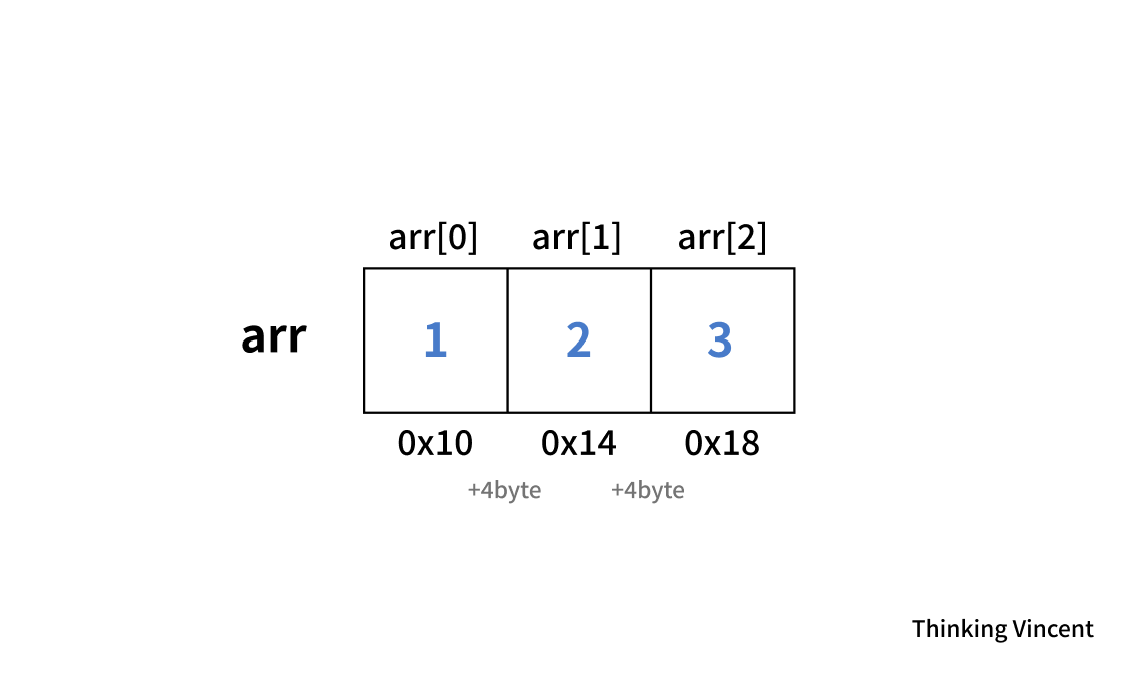
이렇게 생긴 귀여운 int타입 배열이 있다. 여기서 우리가 중앙에 있는 2에 접근하고 싶다면? 어떤 코드를 작성해야할까?

정답은 그냥 arr[1]; 이다.

arr[1] 하나만으로 우리는 2에 접근이 가능하고, 이것은 배열의 사이즈가 어떻든, 접근하고자 하는 위치가 어디이든, 해당 index만 알고 있다면 arr[index]를 통해 접근이 가능하다.

변경(change)은 그냥 접근 한 다음 arr[index] = 변경할 값; 으로 바로 가능하다.

여기까지 배열은 천사였다.

배열에서의 삽입 (insert)

미리 말해 두겠다. 여기서부터 배열은 악마다. 당신을 아주 아주 귀찮게 할 것이고 컴퓨터에게도 힘든 작업을 선물할 것이다.

사이즈에 제약이 발생한 경우

자, 위와 동일하게

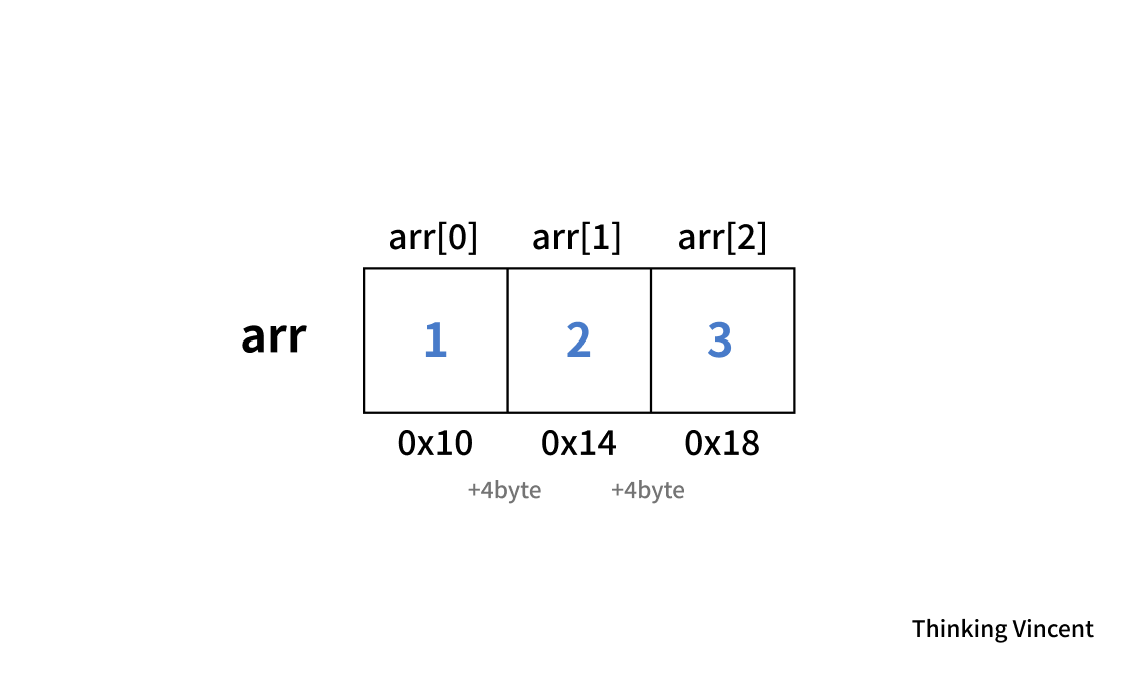
다시 귀여운 int타입 배열이 등장했다. 당신은 3 뒤에 4를 추가하고 싶다. 그런데 어? 이미 꽉 찼는데?
배열의 사이즈를 갑자기 늘릴 수 있던가? 배열의 사이즈는 상수(const)지 않나?
아니지, 잠깐, 저번 시간에 동적으로 사이즈를 설정하는 방법에 대해 배웠었는데... 도대체 어떻게 해야하는거야!

정답은 사이즈가 더 큰 배열을 만들고 기존에 있던 값들을 하나하나 전부 복사한 다음 새로운 값을 추가하는 것이다...

int main() {
	int arr[3] = {1, 2, 3}; // 귀여웠던 배열
   	int arr2[4]; // 4를 넣고 싶어잉
    for (int i = 0; i < 3; ++i) {
    	arr[i] = arr[i]; // 복사 복사...
    }
    arr2[3] = 4; // 오케이 arr2는 1 2 3 4가 되었다.
}

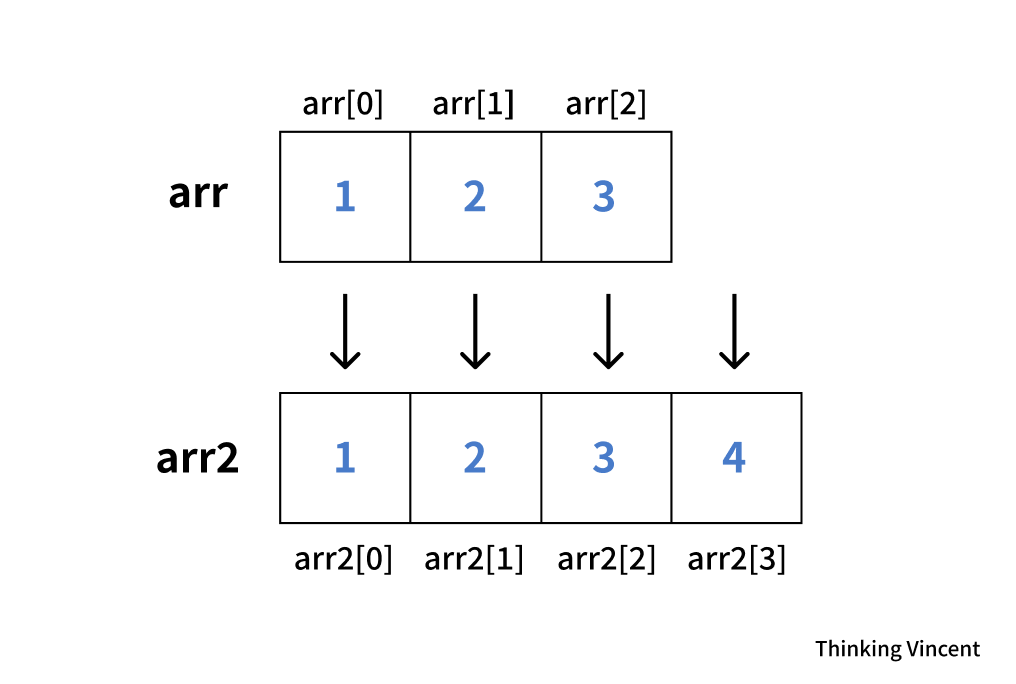
딱 봐도 효율적이지 못 하다. 물론 위 코드는 아주 간단하게만 짠 것이고 실제로는 사용자가 콘솔에서 우리가 미리 만들어둔 insert라는 함수를 호출하면 함수 내부에서 더 큰 사이즈의 배열을 동적으로 만들고 기존의 배열을 복사한 다음... 새로운 값을 추가해줘야 할 것이다. 그리고 이것이 바로 앞 챕터에서 설명했던 "동적 배열(Dynamic Array)"이다! 뒤에서 할 거니까 지금은 잘 몰라도 된다.

지금은 그냥

• 더 큰 사이즈의 새 배열 만들기
• 기존 배열의 값들을 새 배열에 복사
• 새로운 값을 추가

이 프로세스를 이해하면 되겠다.

여기까진 배열이 꽉 찼을 때였다. 하지만 배열이 항상 가득 차 있는 것은 아니다. 실제로는 꽉 차있지 않은 경우에 대부분의 삽입 연산이 일어날 것이다.

사이즈는 괜찮으나 중간에 삽입이 필요할 경우

이번에는 귀여운 배열로 그만 날로 먹고 새로운걸 가져와 보겠다.

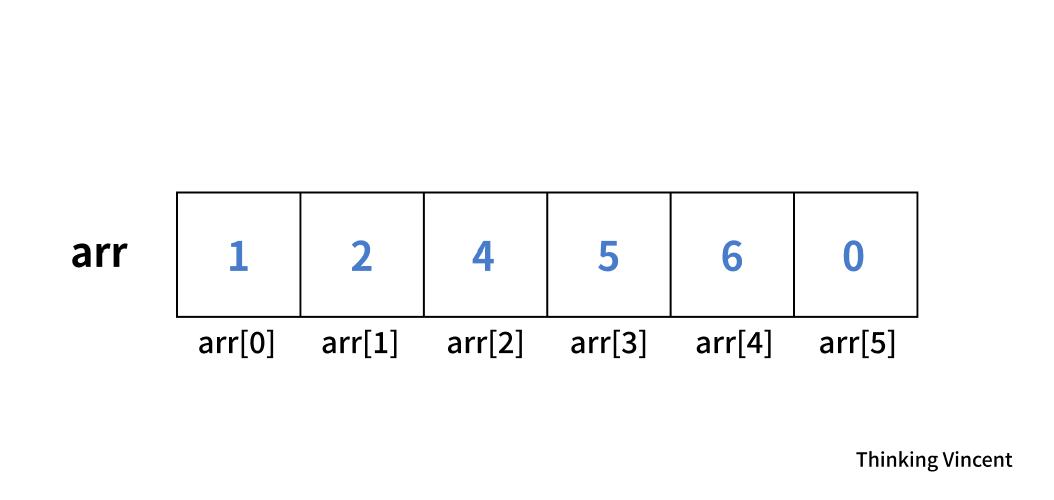
으하하! 무려 사이즈가 6인 int형 배열을 만들어봤다!
1 2 4 5 6 ... 행운의 넘버 3이 없는 것이 마음에 들지 않는다.
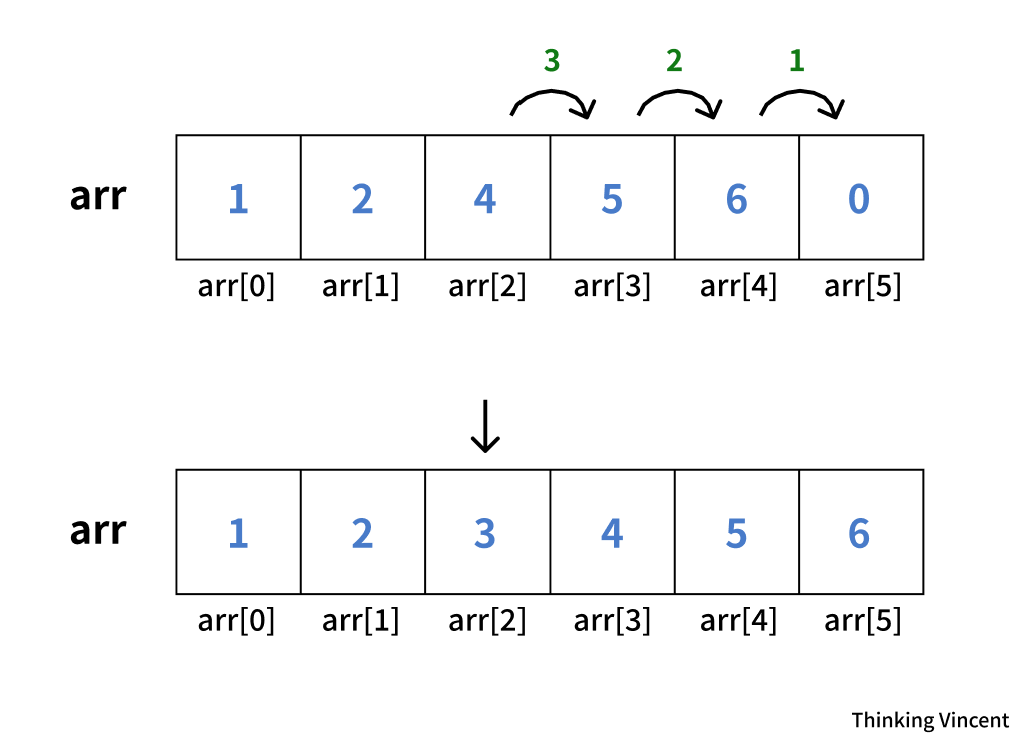
2와 4 사이에 3을 추가하고 싶다. 그럼 어떻게 해야할까?
...
고민의 시간을 주겠다. 참고로 arr[5]에 있는 0은 초기화 당시 들어간 0으로, 값이 없는 것으로 간주하면 된다.
...

정답을 공개한다.
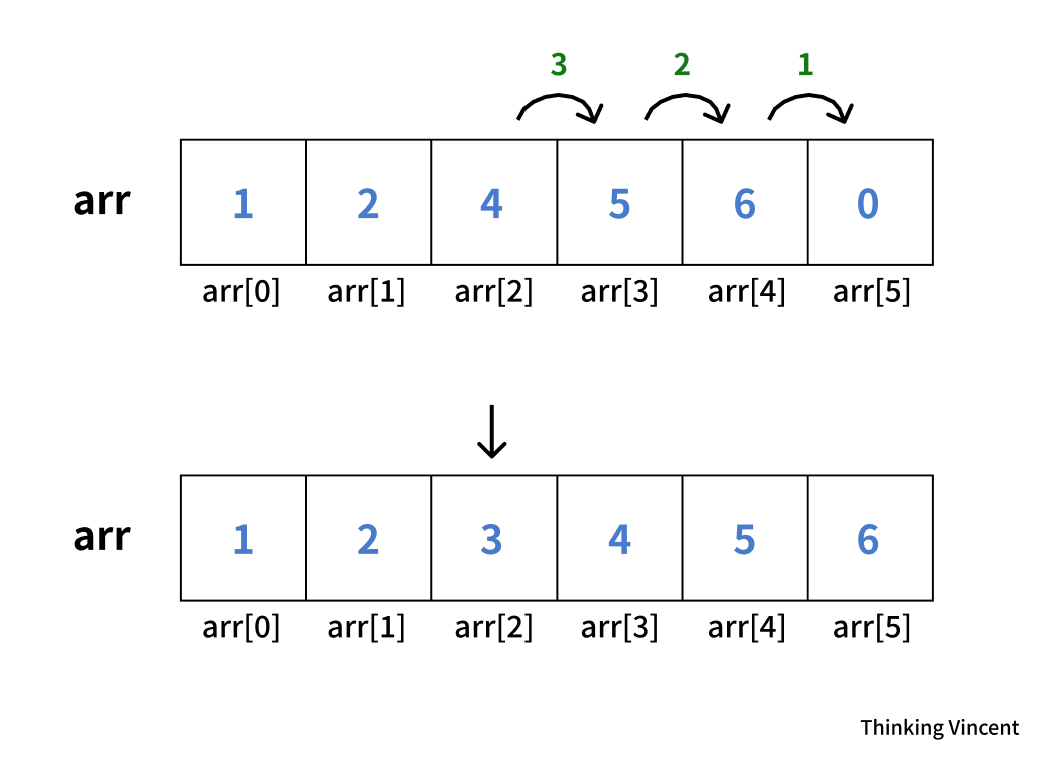
4와 5와 6을 전부 뒤로 한 칸 씩 당기면 된다.

int main() {
    int arr[6] = { 1, 2, 4, 5, 6, 0 };

    for (int i = 4; i >= 2; --i) {
        arr[i + 1] = arr[i];
    } // 원소들을 오른쪽으로 한 칸씩 이동

    arr[2] = 3; // 두 번째 위치에 3을 삽입

    for (int i = 0; i < 6; ++i) {
        cout << arr[i];
    } // 결과 : 1 2 3 4 5 6
}

* 주의할 점
그림과 같이 뒤에서부터 하나씩 오른쪽으로 이동시켜야 한다. 앞에서 부터 시작하면 뒤에 있던 값을 덮어 써버려서 1 2 3 4 4 4와 같은 결과가 나올 것이다. *

배열의 사이즈가 커질 수록, 더 많이 배열의 요소를 오른쪽 또는 왼쪽으로 이동시켜야 할 것이다. 이것을 배열의 "Shift"연산이라 부른다.

Shift 연산은 최악의 경우 현재 배열에 들어 있는 모든 요소를 이동시켜야 하는 비효율을 야기한다.
이를테면 [2, 3, 4, 5, 6, 7, 8, 0]과 같은 배열의 맨 앞에 1을 삽입하고자 하는 경우이다. 그럼 8부터 2까지 모든 수를 뒤로 한 칸씩 Shift하고 그 후에 arr[0] = 1; 을 해야한다.

사이즈도 꽉 찼는데 중간에 삽입을 해야하는 경우

이건 위에서 말한 두 경우를 모두 사용해야한다.

배열에서의 삭제 (delete)

배열에서의 삭제도 삽입과 다르지 않다.
다만 사이즈를 더 크게 만들 이유가 없기 때문에, 삽입에서 방금 배운 Shift연산만 수행해주면 된다. 또한 삭제하고자 하는 원소가 끝에 있어 배열의 순서에 영향을 미치지 않는다면 해당 원소를 0으로 바꾸는 등 삭제 처리를 임의로 해주면 된다.
[1, 2, 3, 4, 5, 6] 여기서 6을 단지 0으로 바꿔주는 것 만으로 삭제 처리를 할 수 있는 것이다.

* 삭제 후 남을 메모리가 아깝다면 동적으로 더 작은 사이즈의 배열을 만들고 복사를 해줘도 된다.

중간에 있는 3을 삭제하고 싶은 경우에는

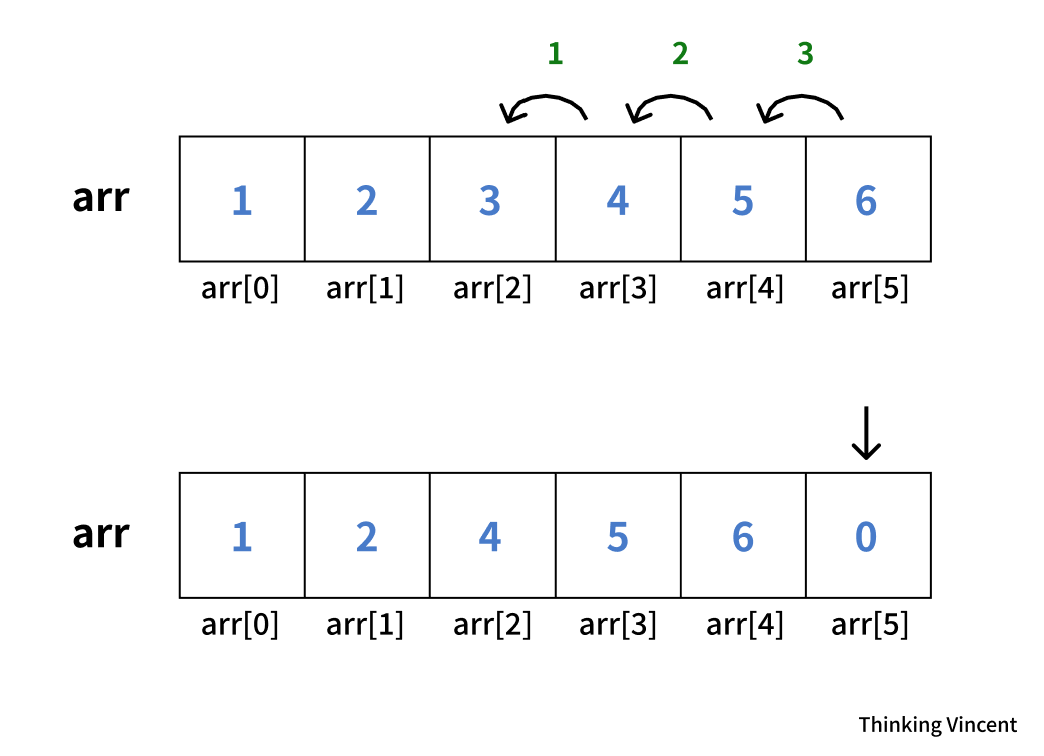
다음과 같이 4 5 6을 좌측으로 한 칸 씩 Shift해주면 된다. 이후 마지막 원소는 0으로 만들어준다.

코드는 한 번 여러분이 직접 해보시기를 바란다! 삽입을 반대로 해준다고 생각하면 된다. 이번에도 화살표의 순서를 유심히 보자.

삭제의 경우에도 최악의 경우 저장된 모든 원소의 수 - 1 만큼 Shift가 일어나게 된다.
가령 [1, 2, 3, 4, 5, 6]의 배열에서 1을 삭제할 경우, 2부터 6까지의 모든 원소를 좌측으로 Shift해야한다. 0번 index에 반드시 값이 있어야 한다는 가정 하에 말이다.

결론

배열은 단순한 index 접근이나 값을 변경할 때 굉장히 수월하다!
index를 통해 한 번에 접근이 가능하다는 것 그 자체가 배열의 가장 큰 장점이다.

그러나 배열에서 삽입과 삭제를 수행할 때, 최악의 경우 모든 원소의 수 수준의 Shift 처리가 필요하다. 이것은 배열의 크기가 커질 수록 더 큰 문제가 될 수 있다. 1000개, 10000개의 shift가 한 번의 삽입과 삭제마다 일어날 수 있는 것이다.

또한 초기에 할당된 size보다 더 많은 size가 필요해질 때, 사이즈가 더 큰 배열을 만들고 기존의 값들을 모두 복사해야 한다. 이 또한 복사가 완료되고 기존 배열이 delete되기 전 까지 컴퓨터는 두 배열에 해당하는 모든 메모리를 보존하고 있어야 하기에 공간적 비효율이 발생한다. 또한 기존 배열의 수 만큼의 복사가 일어나는 것도 시간적 비효율을 야기한다.

따라서, 배열은 접근과 변경이 잦은 프로그램에서는 유리할 수 있으나 삽입과 삭제가 잦은 프로그램에는 적합하지 못 하다.

이러한 단점을 모두 보완해주는 자료구조가 바로

다음 챕터에 등장할 "연결 리스트 (Linked Lists)"이다.

정확한 정보를 전달하기 위해 최선을 다하고 있지만, 그럼에도 부족함을 알고 있습니다. 언제나 피드백을 기다리고 있으니 잘 부탁드립니다!
감사합니다 :)