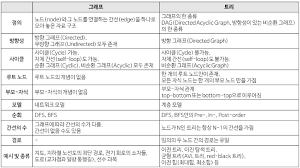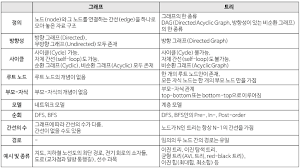
Graph (그래프)
- 그래프의 개념
- 노드(N, Node) 와 그 노드를 연결하는 간선(E, Edge)을 하나로 모아 놓은 자료구조
- 연결되어 있는 객체 간의 관계를 표현할 수 있다
- EX) 지하철 노선도의 최단 경로, 전기 회로의 소자들, 선수 과목 등
- 그래프는 여러 개의 고립된 그래프로 구성될 수 있다. (Isolated Subgraphs)
- 그래프의 특징
- 그래프는 네트워크 모델이다.
- 2개 이상의 경로가 가능 즉, 노드들 사이에 양방항 경로가 가능하다.
- 루트 노드라는 개념이 없다.
- 부모-자식 관계라는 개념이 없다.
- 순회는 DFS/BFS로 이루어진다.
- 그래프는 순환 혹은 비순환이다.
- 그래프는 방향 그래프와 무방향 그래프가 있다.
Tree (트리)
- 트리의 개념
- 트리는 노드로 이루어진 자료 구조다.
- 트리는 하나의 루트 노드를 갖는다.
- 루트 노드를 0개 이상의 자식 노드를 갖고 있다.
- 반복적으로 그 자식 노드 또한 0개 이상의 자식 노드를 갖는다.
- 각 노드(Node)들을 연결하는 선을 간선(Edge)이라고 한다.
- 트리에는 사이클이 존재할 수 없다.
- 각 노드는 부모 노드로의 연결이 있을 수도, 없을 수도 있다.
- 각 노드는 어떤 자료형으로도 표현이 가능하다.
- 비선형 자료구조로 계층적 관계를 표현한다.
- 그래프의 한 종류이다.
- 트리의 특징
- 그래프의 한 종류로 '최소 연결 트리' 라고도 불린다.
- 트리는 계층 모델이다.
- 트리는 DAG(Directed Acyclic Graphs, 방향성이 있는 비순환 그래프)의 한 종류(즉, 사이클이 없다)이다.
- 노드가 N개인 트리는 항상 N-1rodml 간선을 가진다.
- 임의의 두 노드 간의 경로는 유일하다. (두 개의 정점 사이 1개의 경로만)
- 모든 자식 노드는 한 개의 부모 노드만을 가진다.
- 부모-자식 관계이므로 흐름은 top-bottom or bottom-top으로 이루어짐
- 순회는 Pre-order/In-order/Post-order로 이루어진다.
- 트리는 이진 트리, 이진 탐색 트리, 균형 트리, 이진 힙 등이 있다.