💡 완전탐색으로 경우의 수를 풀 수 있는 알고리즘 중 조합에 대해 공부해보자.
개요 🛫
조합(Combination)은 보통 모든 경우의 수를 탐색해서 해를 찾을때 사용된다. (완전탐색)
아주 아주 기본적인 이론이므로 머릿속에 넣어두자 👍🏽
학습 내용 📖
조합(Combination)
정의
서로 다른 n개의 원소 중에서 r개를 중복없이 순서에 상관 없이 선택 혹은 나열하는 것 nCr

이미지 : 조합 공식
예시
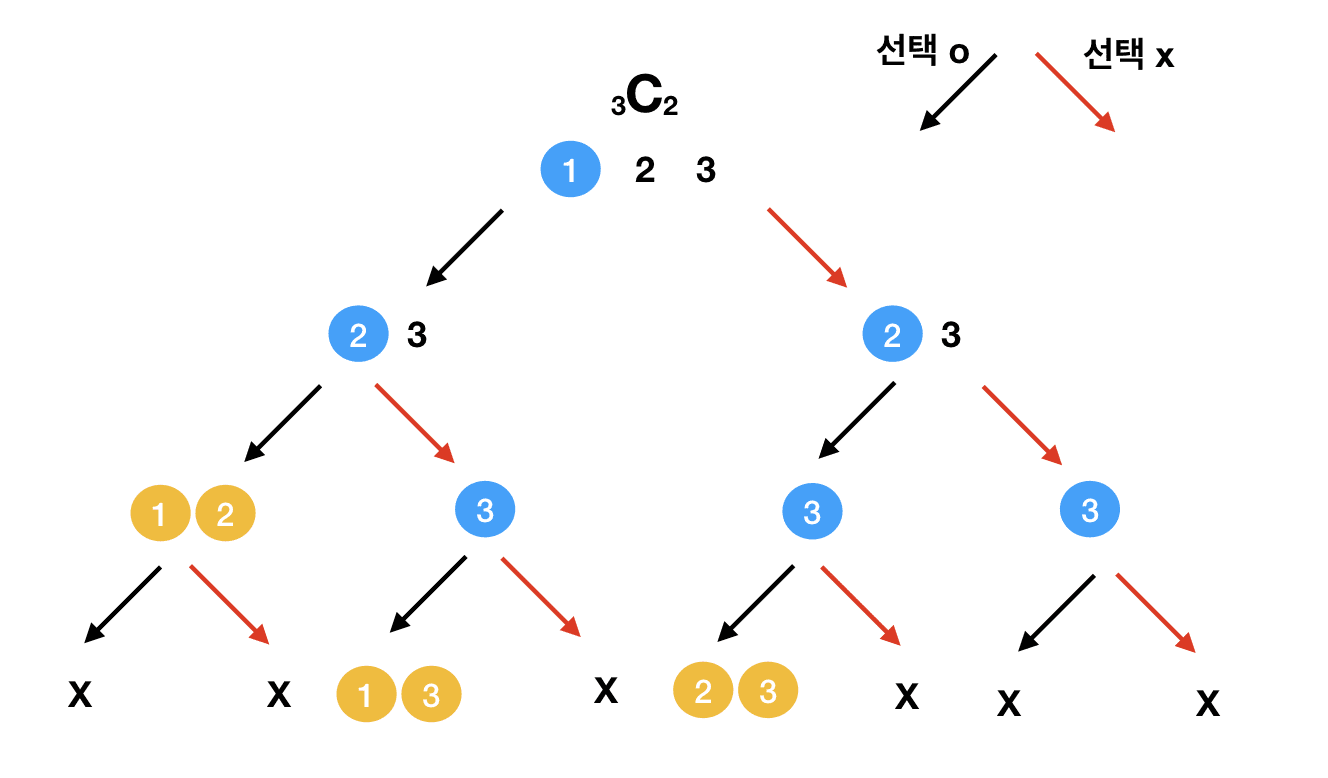
(1, 2, 3) 의 집합에서 3(모든)개의 조합을 구하는 경우 3C3
아래의 그림처럼 요소를 선택하고 선택한 요소들을 제외한 나머지 요소가 선택될 수 있는 경우의 수들을 분개하여 나열한다.
예제 코드 1 (For Loop)
let input = [1, 2, 3, 4];
let count = 0;
function combination(arr) {
for (let i = 0; i < arr.length; i++) {
for (let j = i + 1; j < arr.length; j++) {
count++;
}
}
}
combination(input);
console.log(count);이런 방식의 중첩 for문으로 코드를 짜면 input 요소의 개수(뽑을 개수)가 커질 수록 for 문의 depth가 .. 아주 커진다.
그래서 순열이나 조합을 구하는 알고리즘에서는 재귀 함수(Recursion)를 이용한다.
예제 코드 2 (Recursion) 👍🏽
let input = [1, 2, 3, 4];
let output = [];
let count = 0;
// arr : input 데이터 , data : output 데이터, s : 시작 인덱스, idx : 현재 위치정보, r : 선택 개수
function combinationRecursion(arr, data, s, idx, r) {
if (s === r) {
count++;
console.log(data);
return;
}
for (let i = idx; arr.length - i >= r - s; i++) {
data[s] = arr[i];
combinationRecursion(arr, data, s + 1, i + 1, r); // Recursion
}
}
combinationRecursion(input, output, 0, 0, 2); // Main Call
console.log(count);
위 예제를 보면 요소의 개수가 길어져도 for문을 추가해주지 않아도 된다.
예제 코드2를 분석해보자.
4C2
1 Loop (Main Call, i = 0)
-Call Value
arr: [1, 2, 3, 4]data: []s: 0idx: 0r: 2
-For Loop Value
i = idx: 0arr.length - i >= r - s: 4 >= 2 (4 - 0 >= 2 - 0)s: 0idx: 0data[s] = arr[i]: data[0] = arr[0] => [1]combinationRecursion(arr, data, s + 1, i + 1, r): combinationRecursion(arr, [1], 1, 1, 2)
1 Loop 1 Recursion(ReCall)
-Call Value
arr: [1, 2, 3, 4]data: [1]s: 1idx: 1r: 2
-For Loop Value
i = idx: 1arr.length - i >= r - s: 3 >= 1 (4 - 1 >= 2 - 1)s: 1idx: 1data[s] = arr[i]: data[1] = arr[1] => [1, 2]combinationRecursion(arr, data, s + 1, i + 1, r): combinationRecursion(arr, [1, 2], 2, 2, 2)
1 Loop 2 Recursion(Re:ReCall)
-Call Value
arr: [1, 2, 3, 4]data: [1, 2]s: 2idx: 2r: 2
-return
count ++output = [1, 2]
2 Loop 1 Recursion(Return)
-For Loop Value
i: 2arr.length - i >= r - s: 2 >= 1 (4 - 2 >= 2 - 1)s: 1idx: 1data[s] = arr[i]: data[1] = arr[2] => [1, 3]combinationRecursion(arr, data, s + 1, i + 1, r): combinationRecursion(arr, [1, 3], 2, 3, 2)
2 Loop 2 Recursion(Re:ReCall)
-Call Value
arr: [1, 2, 3, 4]data: [1, 3]s: 2idx: 3r: 2
-return
count ++output = [1, 3]
3 Loop 1 Recursion(Return)
-For Loop Value
i: 3arr.length - i >= r - s: 1 >= 1 (4 - 3 >= 2 - 1)s: 1idx: 1data[s] = arr[i]: data[1] = arr[3] => [1, 4]combinationRecursion(arr, data, s + 1, i + 1, r): combinationRecursion(arr, [1, 4], 2, 4, 2)
3 Loop 2 Recursion(Re:ReCall)
-Call Value
arr: [1, 2, 3, 4]data: [1, 4]s: 2idx: 4r: 2
-return
count ++output = [1, 4]
4 Loop 1 Recursion(Return)
-For Loop Value
i: 4arr.length - i >= r - s: 0 >= 1 (4 - 4 >= 2 - 1) => for loop end, return
2 Loop (Main Call, i = 1)
-For Loop Value
i: 1arr.length - i >= r - s: 3 >= 2 (4 - 1 >= 2 - 0)s: 0idx: 0data[s] = arr[i]: data[0] = arr[1] => [2]combinationRecursion(arr, data, s + 1, i + 1, r): combinationRecursion(arr, [2], 1, 2, 2)
2 Loop 1 Recursion(ReCall)
-Call Value
arr: [1, 2, 3, 4]data: [2]s: 1idx: 2r: 2
-For Loop Value
i = idx: 2arr.length - i >= r - s: 2 >= 1 (4 - 2 >= 2 - 1)s: 1idx: 2data[s] = arr[i]: data[1] = arr[2] => [2, 3]combinationRecursion(arr, data, s + 1, i + 1, r): combinationRecursion(arr, [2, 3], 2, 3, 2)
2 Loop 2 Recursion(Re:ReCall)
-Call Value
arr: [1, 2, 3, 4]data: [2, 3]s: 2idx: 3r: 2
-return
count ++output = [2, 3]
...
위와 같이 해를 찾는 도중 해가 아니어서 막히면, 되돌아가서 다시 해를 찾아가는 기법을
백트래킹이라고한다.
재귀 함수는 빈번히 활용되므로 내부 로직의 이해를 잘 해야한다 💡

45C6 일 때,
45! / ( 6! * (45-6)! )
위와 같이 계산하면 머리 아프니까!
더 간단하고, 힘이 적게 들게 계산
45 / 1 × 44 / 2 × 43 / 3 × 42 / 4 × 41 / 5 × 40 / 6 = 8145060
45 / 1 은 쓸데없는 짓이지만, Factorial 이 원래 이론상 쓸데없이 1도 곱하는 거라서.
더 간단히,
45 × 44 / 2 × 43 / 3 × 42 / 4 × 41 / 5 × 40 / 6 = 8145060