💡 완전탐색으로 경우의 수를 푸는 알고리즘 중 순열에 대해 공부해보자.
개요 🛫
순열(Permutation)은 보통 모든 경우의 수를 탐색해서 해를 찾을때 사용된다. (완전탐색)
아주 아주 기본적인 이론이므로 머릿속에 넣어두자 👍🏽
학습 내용 📖
순열(Permutation)
정의
서로 다른 n개의 원소 중에서 r개를 중복없이 순서에 상관있게 선택 혹은 나열하는 것 nPr
- 서로 다른 n개
- 중복을 허락하지 않고
- 나열하는 수
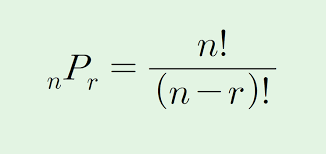
이미지 : 순열 공식
예시
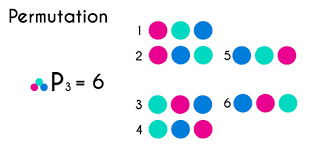
(1, 2, 3) 의 집합에서 3(모든)개의 순열을 구하는 경우 3P3
아래의 그림처럼 요소를 선택하고 선택한 요소들을 제외한 나머지 요소가 선택될 수 있는 경우의 수들을 분개하여 나열한다.

프로그래밍 관점에서 순열은 선택할 인덱스와 교환될 인덱스를
SWAP하는 과정을 반복하여 순열을 만들 수 있다.
이게 무슨 얘기냐면..
최초 (1, 2, 3) 의 집합에서
1 선택 (1, )
1 선택된 상태에서 2 선택 (1, 2, 3)
1 선택된 상태에서 2와 3 스왑 (1, 3, 2)
1과 2 스왑으로 2 선택 (2, ).. 아래 예제 코드로 이해해보자..
예제 코드 1 (For Loop)
let input = ["a", "b", "c"];
let count = 0;
function permutation(arr) {
// for i -> 첫 번째 index 위치시킬 요소 a or b or c [i, 0, 0]
for (let i = 0; i < arr.length; i++) {
// for j -> 두 번째 index 위치시킬 요소 [i, j, 0]
for (let j = 0; j < arr.length; j++) {
if (i === j) continue;
// for j -> 세 번째 index 위치시킬 요소 [i, j, k]
for (let k = 0; k < arr.length; k++) {
if (i === k) continue;
if (j === k) continue;
console.log(arr[i], arr[j], arr[k]);
count++;
}
}
}
}
permutation(input);
console.log(count);이런 방식의 중첩 for문으로 코드를 짜면 input 요소의 개수가 커질 수록 for 문의 depth가 .. 어마어마해질 것이다.
그래서 순열이나 조합을 구하는 알고리즘에서는 재귀 함수(Recursion)를 자주 이용한다.
예제 코드 2 (Recursion) 👍🏽
let input = ["a", "b", "c"];
let count = 0;
// s = 시작 위치 , r = 뽑을 개수 (인덱스 기준)
function permutation(arr, s, r) {
// 1. 재귀 함수를 멈춰야할 조건
if (s === r) {
count++;
console.log(arr.join(" ")); // 배열의 상태 출력
return; // 재귀 탈출
}
// 2. 재귀를 돌면서 수행되는 부분 (main logic)
for (let i = s; i < arr.length; i++) { // i가 0부터 돌면 중복하면서 뽑음
[arr[s], arr[i]] = [arr[i], arr[s]] // SWAP
permutation(arr, s + 1, r); // s 값을 증가시켜서 다음 인덱스를 선택하게
[arr[s], arr[i]] = [arr[i], arr[s]] // SWAP 원상 복귀
}
}
permutation(input, 0, 2);
console.log(count);위 예제를 보면 요소의 개수가 길어져도 for문을 추가해주지 않아도 된다.
예제 코드2의 스왑 부분을 분석해보자.
1) s = 0, r = 2 (i = 0, s = 0) 이기때문에 SWAP을 해도 "A"를 선택 : ["a", ]
2) 재귀로 들어가면서 s + 1
3) s = 1, r = 2 (i = 1, s = 1) 이기때문에 SWAP을 해도 "B"를 선택 : ["a", "b", ]
4) 재귀로 들어가면서 s + 1
5) s = 2, r = 2 (i = 2, s = 2) 이기때문에 남은 "C"를 선택 : ["a", "b", "c"]
...
1) s = 1, r = 2 (i = 2, s = 1) 이기때문에 SWAP을 해서 "C"를 선택 : ["a", "c", ]
2) s = 2, r = 2 (i = 2, s = 2) 이기때문에 남은 "B"를 선택 : ["a", "c", "b"]
return 으로 재귀 함수 탈출
재귀 밖 for문의 i++
1) s = 0, r = 2, i = 1 이기때문에 SWAP을 해서 "B"를 선택 : ["b", ]
...
return 으로 재귀 함수 탈출
재귀 밖 for문의 i++
1) s = 0, r = 2, i = 2 이기때문에 SWAP을 해서 "C"를 선택 : ["c", ]
...
return 으로 재귀 함수 탈출
console.log 찍고 종료
위와 같이 해를 찾는 도중 해가 아니어서 막히면, 되돌아가서 다시 해를 찾아가는 기법을
백트래킹이라고한다.
재귀 함수는 빈번히 활용되므로 내부 로직의 이해를 잘 해야한다 💡