💡 점화식(재귀식)인 등차수열, 등비수열, 팩토리얼을 예제를 통해 공부해보자
개요 🛫
점화식은 재귀식이라고도 말하는데, 대표적인 예로 피보나치 수열이 있다. 이런 녀석들은 기본적인 for Loop로 풀어도 되지만,,
피보나치 수열은 재귀함수로 풀어야한다. + 재귀함수에 익숙해지기 위해 가능한 재귀형태로 풀어보고자 한다.
매일 연습해서 익숙해지면 더 복잡한 알고리즘도 풀 수 있게 될 것이다. 👍🏽
학습 내용 📖
점화식(Recurrence Relation)
정의
수열에서 이웃하는 두개의 항 사이에 성립하는 관계를 나타낸 관계식
예시
- 등차 수열
- 등비 수열
- 팩토리얼
- 피보나치 수열

등차/등비 수열
등차 수열의 뜻
수학에서, 등차수열은 연속하는 두 항의 차이가 모두 일정한 수열을 뜻한다.
예를 들어 1, 3, 5, 7, 9, ...은 등차수열이다.
이때 두 항의 차이는 이 수열의 모든 연속하는 두 항들에 대해서 공통적으로 나타나는 차이므로, 공차라고 한다.
F(n) = F(n-1) + a
*a는 공차
예제 코드 1
let result;
function recursive(s, a, number) {
if (number === 1) {
return s;
}
return recursive(s + a, a, number - 1);
};
result = recursive(5, 3, 5);
console.log(result);
// 5 등차수열 2간격 3회 = 5 + 2 + 2 + 2 = 11
// 5 등차수열 3간격 5회 = 5 + 3 + 3 + 3 + 3 + 3 = 20
// number : 5 , recursive(5 + 3, 3, 5);
// number : 4 , recursive(8 + 3, 3, 4);
// number : 3 , recursive(11 + 3, 3, 3);
// number : 2 , recursive(14 + 3, 3, 2);
// number : 1 , 17 반환
// 5 3 5
// 8 3 4
// 11 3 3
// 14 3 2
// 17 3 1재귀함수에 더한 값을 파라미터로 호출, 반복되는 형식의 예제 풀이
예제 코드 2 👍🏽
let result;
function recursive2(s, a, number) {
if (number === 1) {
return s;
}
return recursive2(s, a, number - 1) + a;
};
result = recursive2(3, 2, 5);
console.log(result);
재귀함수에 값을 더해서 반복되는 형식의 예제 풀이
베스트
등비 수열의 뜻
등비수열 또는 기하수열은 각 항이 초항과 일정한 비를 가지는 수열을 말하며, 일정한 비를 공비라고 한다.
F(n) = F(n-1) * a
*a는 공비
예제 코드
let result;
function recursive(s, t, number) {
if (number === 1) {
return s;
}
return recursive(s, t, number - 1) * t;
};
result = recursive(3, 2, 5);
console.log(result);재귀함수에 값을 곱, 반복되는 형식의 예제 풀이 등차 수열에 연산자만 바꿔준 형식이다.
팩토리얼
팩토리얼의 뜻
보다 작거나 같은 모든 양의 정수의 곱이다.
n이 하나의 자연수일 때, 1에서 n까지의 모든 자연수의 곱을 n에 상대하여 이르는 말이다. 기호는 !을 쓰며 팩토리얼이라고 읽는다.
a! = (a - 1) (a - 2) (a - n)...
예제 코드
let result;
function factorial(number) {
if (number === 1) {
return 1;
}
return factorial(number - 1) * number;
}
result = factorial(5);
console.log(result);
// 5! = 5 * 4 * 3 * 2 * 1함수의 리턴 값에 재귀 함수에 number을 곱해 반환하는 재귀함수
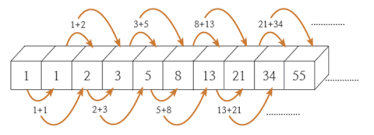
피보나치 수열 (Fibonacci numbers)
피보나치 수열의 뜻
수학에서, 피보나치 수는 첫째 및 둘째 항이 1이며 그 뒤의 모든 항은 바로 앞 두 항의 합인 수열이다.
1, 1, 2, 3, 5, 8, 13, 21
예제 코드
let result;
function fibonacci(number) {
if (number === 1 || number === 0) {
return number;
}
console.log(number);
return fibonacci(number - 1) + fibonacci(number - 2);
}
result = fibonacci(6); // 파라미터는 원하는 피보나치 수열의 항
console.log(result)
// > 1, 1, 2, 3, 5, 8, 13, 21f(6) = f(5) + f(4) : 8
f(5) = f(4) + f(3) : 5
f(4) = f(3) + f(2) : 3
f(3) = f(2) + f(1) : 2
f(2) = 1 + 0 : 1
f(1) = 1
느낀점💡
백트래킹을 위해 재귀함수를 계속 사용하며 익히고 있다..
😿😿 재귀함수를 이해하는게 쉽지 않다.. 사용을 하면서 내부 로직이 어떻게 돌아가는지 체크를 하는 중인데, 자주 사용하다보면 더 익숙해질 것이라고 믿는다