딥러닝 초짜가 직접 뜯어보다. - 로지스틱 회귀

잘못 예측하면 모델들도 저렇게 얻어맞는다.

저번 글에서는 선형 회귀 분석에 관한 실습 코드를 하나하나 뜯어보았다. 이번에는 선형이 아닌 '시그모이드'라고도 불리는 로지스틱 회귀에 대해 뜯어보도록 하겠다.

---

선형 회귀분석과 다른 점

Linear Regression이라고도 불리는 선형 회귀분석은 불균형한 데이터에 대해 잘 대응하지 못한다. 예를 들어, 청소년이냐 아니냐라는 값의 0 과 1을 얻고 싶은데, 이 사이의 실수값으로 예측이 될 수 있기 때문에 이러한 데이터에 대해 잘 대응하지 못한다.

Logistic Regression, 또는 로지스틱 회귀는 이러한 한계점을 잘 극복했으며 시그모이드 함수를 추가로 사용한다.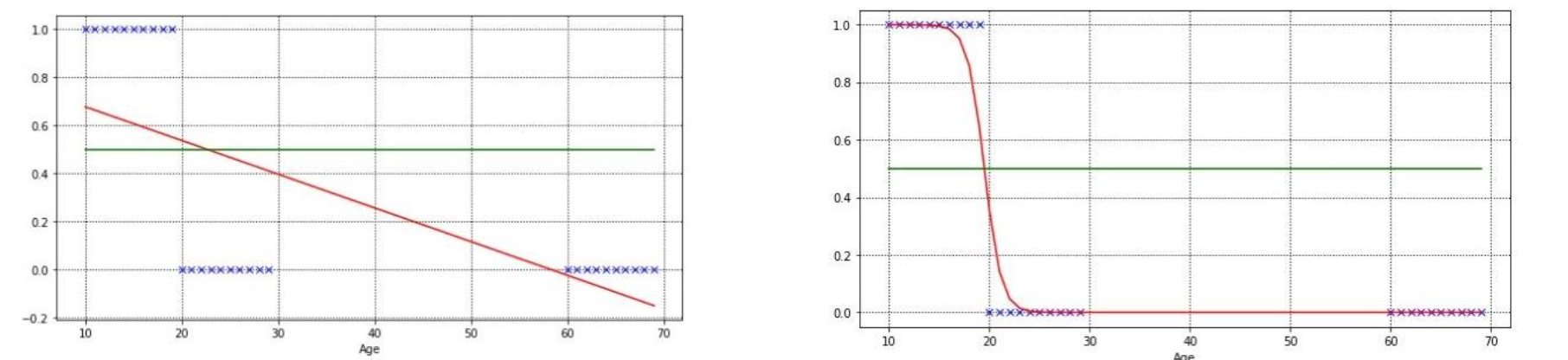

---

로지스틱 회귀 뽀개기

똑같이 실습코드를 하나하나 내 눈높이에서 뽀개보겠다.

import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim

class LogisticRegression(torch.nn.Module): 
  def __init__(self):
    super().__init__() 
    self.linear = nn.Linear(2,1) 
    
  def forward(self, x): 
    outputs = torch.sigmoid(self.linear(x))
    return outputs 
  
  def predict_proba(self, x):
    return self.forward(x)

  def predict(self, x): 
    return np.where(self.forward(x) >= 0.5, 1, 0)

자...뭐가 많이 추가됐다. 뭔소린지 하나도 모르겠으니, 첫줄부터 차근차근 살펴보자.

일단 로지스틱 회귀 모델을 만들어야 하므로 생성자를 만든다. 이 떄 self.linear = nn.Linear(2,1) 은 2차원을 입력받는 입력층과, 1차원을 출력하는 출력층으로 이루어진 신경 계층망을 생성하겠다는 말이다. nn.~ 이 부분이 PyTorch에서 신경망 구축을 담당하는 함수라고 한다.

forward(self, x)는 데이터를 이 신경망에 입력하여 최적화하는, 더 쉽게 내 언어로 말하면 데이터들을 이 신경망에 거쳐 지나가게 하는 함수라고 한다.

predict_proba(self,x)는 평가용 함수, predict(self,x)는 실제 예측을 담당하는 함수다.

여기서 동기 형한테 추가로 배운 점이 있는데, 현재 위의 코드는 단층 신경망으로 이루어져 있다. 한마디로 신경 계층망이 딱 한 개 밖에 없는 단순한 구조다. 만약 중간에 신경층을 추가로 삽입하고 싶으면 위의 self.linear을 다음과 같이 바꾸면 된다.

self.stack = nn.Sequential( # 심층 신경망
        nn.Linear(1000, 512), # 단계별로 input dim, output dim 정함
        nn.ReLU(), # 활성화 함수 종류 중 ReLU()를 사용하여 변환
        nn.Linear(512, 64), # 반복
        nn.ReLU(),
        nn.Linear(64,8),
        nn.ReLU(),
        nn.Linear(8,1),
        nn.Sigmoid() # 시그모이드를 통해 변환 (중간 단계에서 사용하는 활성화 함수는 ReLU(), 마지막은 sigmoid(), 중간에 sigmoid()하면 문제 발생 가능)
    )

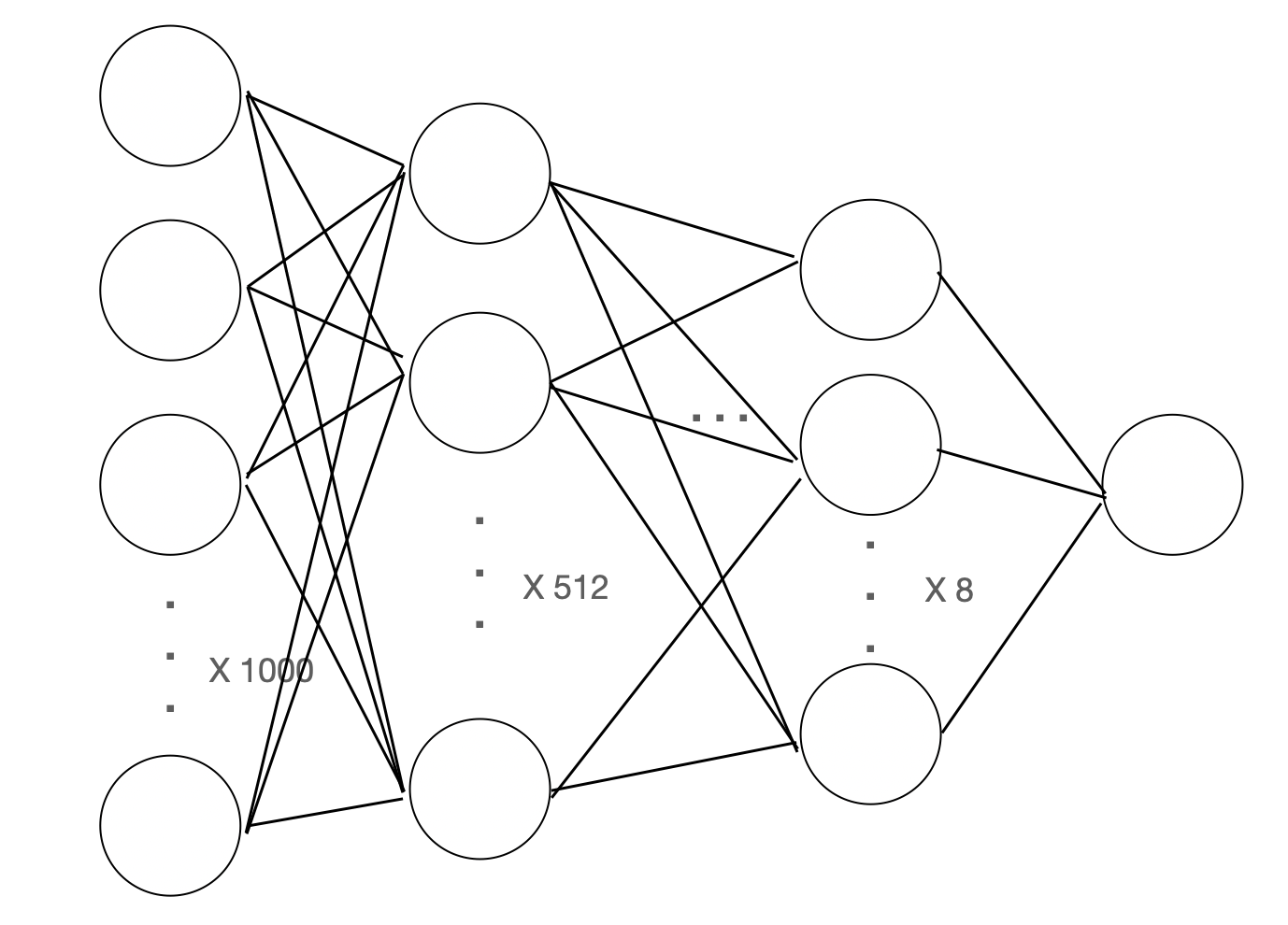
self.linear대신 self.stack으로 바뀐 것을 알 수 있다. 이름 그대로 신경층을 쌓아올린 형식이다. 위의 이미지처럼 말이다. nn.Linear()이 겹겹마다 있고 그 사이에는 nn.ReLU()가 있는데, 동기 형에 따르면 중간 단계에서 사용하는 활성화 함수는 nn.ReLU()를 사용하고, 마지막 단계에서는 nn.Sigmoid()를 사용하여 최종 결과값을 도출한다고 한다. 그 이유는 중간 단계에서 sigmoid() 함수를 사용하면 오류가 발생할 수 있다고 한다.

추가로 신경 노드는 각 단계별로 8의 배수가 제일 적절하다고 한다. 가장 최적화가 잘 되는 조건이라고 하므로 그러러니 하고 넘어가자.

class Config: 
  seed = 42 
  learning_rate = 0.03 
  epochs = 10000

torch.manual_seed(Config.seed)
x_data =  [[1.7, 0.3], [1.3, 0.2], [2.0, 0.3],[2.4, 0.4], [3.0,0.7], [4.0,0.8], [3.5,0.7]]
y_data =  [[0], [0], [0], [1], [1], [1], [1]]
x_train = torch.FloatTensor(x_data)
y_train = torch.FloatTensor(y_data)

model = LogisticRegression()

optimizer = optim.SGD(model.parameters(), lr=Config.learning_rate)

for epoch in range(Config.epochs + 1):

    predict = model(x_train) 

    cost = torch.nn.functional.binary_cross_entropy(predict, y_train)

    optimizer.zero_grad()
    cost.backward()
    optimizer.step()

    if epoch % (Config.epochs//10) == 0:
        print('Epoch {:4d}/{} Cost: {:.6f}'.format(
            epoch, nb_epochs, cost.item()
        ))

이전 글과 다르게 입력 값의 차원이 1차원이 아닌 2차원의 텐서로 이루어져있다. 우리는 로지스틱 회귀 모델을 사용할 것이므로 model=LogisticRegression()을 통해 모델을 생성한다. 이전 글에서 다뤘다시피 optimizer을 통해 최적화할 준비를 끝낸다.

이번엔 cost에서 좀 낯선 함수가 있다. torch.nn.functoinal.binary_cross_entropy인데, 이진 교차 엔트로피라고 불리며 손실 함수의 일종이다. 우리가 사용하는 모델은 로지스틱 회귀 모델인데, 이 모델은 결과를 0또는 1, 한마디로 단 두개의 결과로 분류를 하는 이진 분류를 사용한다. 이런 경우에서 사용하는 비용 측정 방법이 Binary Cross Entropy이다. 아직 뭔 소린지 모르겠으니 조금 더 쉽게 설명해보자.

---

Binary Cross Entropy

어떤 모델이 강아지와 고양이를 분류한다고 가정하자. 예측 결과는 단 두개다. 강아지냐, 고양이냐. 강아지와 고양이 그 사이의 무언가는 없다. 한 마디로 확률이 단 두 경우, 0 또는 1이란 말이다.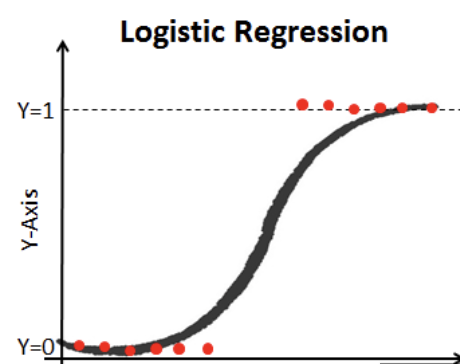
Y = 0을 강아지, Y=1을 고양이라고 하자. 0과 1 사이에 어떠한 빨간 점도 없다는 것이 보이는가? 가운데 시그모이드 함수선을 경계로 단 두 영역으로 정확히 나누어진 것을 볼 수 있다. 그럼 이 모델이 강아지를 고양이라고 잘못 예측하고, 고양이를 강아지라고 잘못 예측할 경우에 패널티를 주어야 하는데, 저 이미지를 보면 경계선과 빨간 점 사이의 거리가 기하 급수적으로 증가하는 것이 보일 것이다. 그 거리를 함수로 나타내면 로그로 표현할 수 있다.

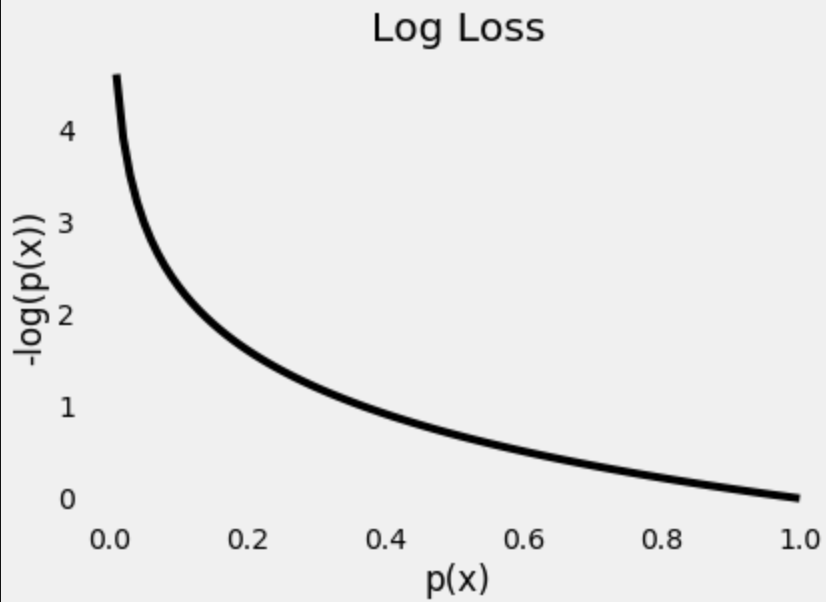
예측과 실제 값이 일치할 확률이 1일 수록 손실은 0에 가까워지며 반대로 예측값이 실제와 다를 확률, 즉 예측 확률(p(x))이 0에 가까워 질수록 손실 값이 기하급수적으로 증가함을 알 수 있다.

모델이 어떤 강아지를 보고 '이 녀석은 고양이일 확률이 99%입니다!' 이러는 순간 패널티가 무자비하게 증가한다는 것이다. 0.01이니 손실 비용이 거의 천장을 뚫을 것이다. 그럼 그 예측 값을 보고 모델은 기겁하며 황급히 자신의 예측을 강아지로 바꿀 것이다. 이렇게 최적화를 진행한다.

---

최종 결과

with torch.no_grad():
  x_test = torch.FloatTensor([[1.5,0.2], [4.1,0.7], [3.2, 0.9]])
  predict = model.predict(x_test)
  predict_proba = model.predict_proba(x_test) # 평가용
  print(predict_proba)
  print(predict)
  
import seaborn as sns 
from matplotlib import pyplot as plt 

fig, axes = plt.subplots(figsize=(8,4))

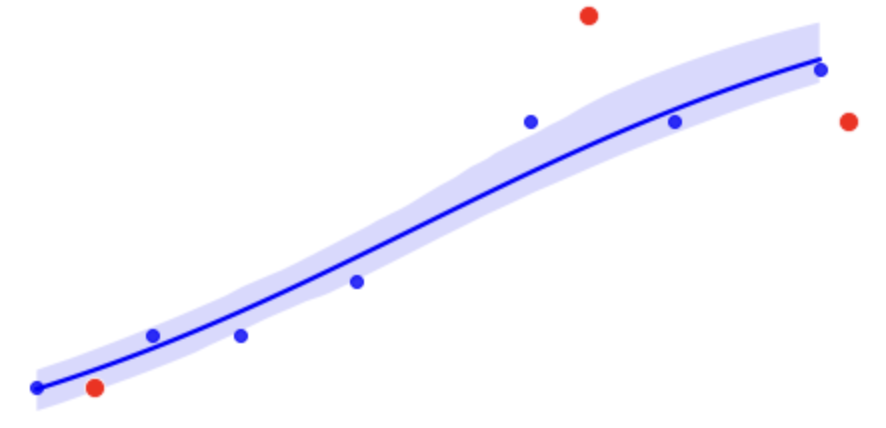
sns.regplot(x_train[:,0].squeeze().cpu().numpy(), x_train[:,1].squeeze().cpu().numpy(), logistic=True, color='blue', ax = axes)
sns.scatterplot(x_test[:,0].squeeze().cpu().numpy(), x_test[:,1].squeeze().cpu().numpy(), color='red', s=100, ax = axes)

10000번의 학습을 통해 이전 글과 같이 새로운 평가용 데이터(빨간 점)을 추가하여 예측한 결과, 다음과 같이 나온다.