문제
수빈이는 동생과 숨바꼭질을 하고 있다. 수빈이는 현재 점 N(0 ≤ N ≤ 500,000)에 있고, 동생은 점 K(0 ≤ K ≤ 500,000)에 있다. 수빈이는 걷거나 순간이동을 할 수 있다. 만약, 수빈이의 위치가 X일 때 걷는다면 1초 후에 X-1 또는 X+1로 이동하게 된다. 순간이동을 하는 경우에는 1초 후에 2*X의 위치로 이동하게 된다. 동생은 항상 걷기만 한다. 동생은 항상 매 초마다 이동을 하며, 이동은 가속이 붙는다. 동생이 이동하는 거리는 이전에 이동한 거리보다 1을 더한 만큼 이동한다. 즉, 동생의 처음 위치는 K, 1초가 지난 후 위치는 K+1, 2초가 지난 후 위치는 K+1+2, 3초가 지난 후의 위치는 K+1+2+3이다.
수빈이와 동생의 위치가 주어졌을 때, 수빈이가 동생을 찾을 수 있는 가장 빠른 시간이 몇 초 후인지 구하는 프로그램을 작성하시오. 동생을 찾는 위치는 정수 좌표이어야 하고, 수빈이가 0보다 작은 좌표로, 50만보다 큰 좌표로 이동하는 것은 불가능하다.
입력
첫 번째 줄에 수빈이가 있는 위치 N과 동생이 있는 위치 K가 주어진다. N과 K는 정수이다.
출력
수빈이가 동생을 찾는 가장 빠른 시간을 출력한다. 수빈이가 동생을 찾을 수 없거나, 찾는 위치가 500,000을 넘는 경우에는 -1을 출력한다.
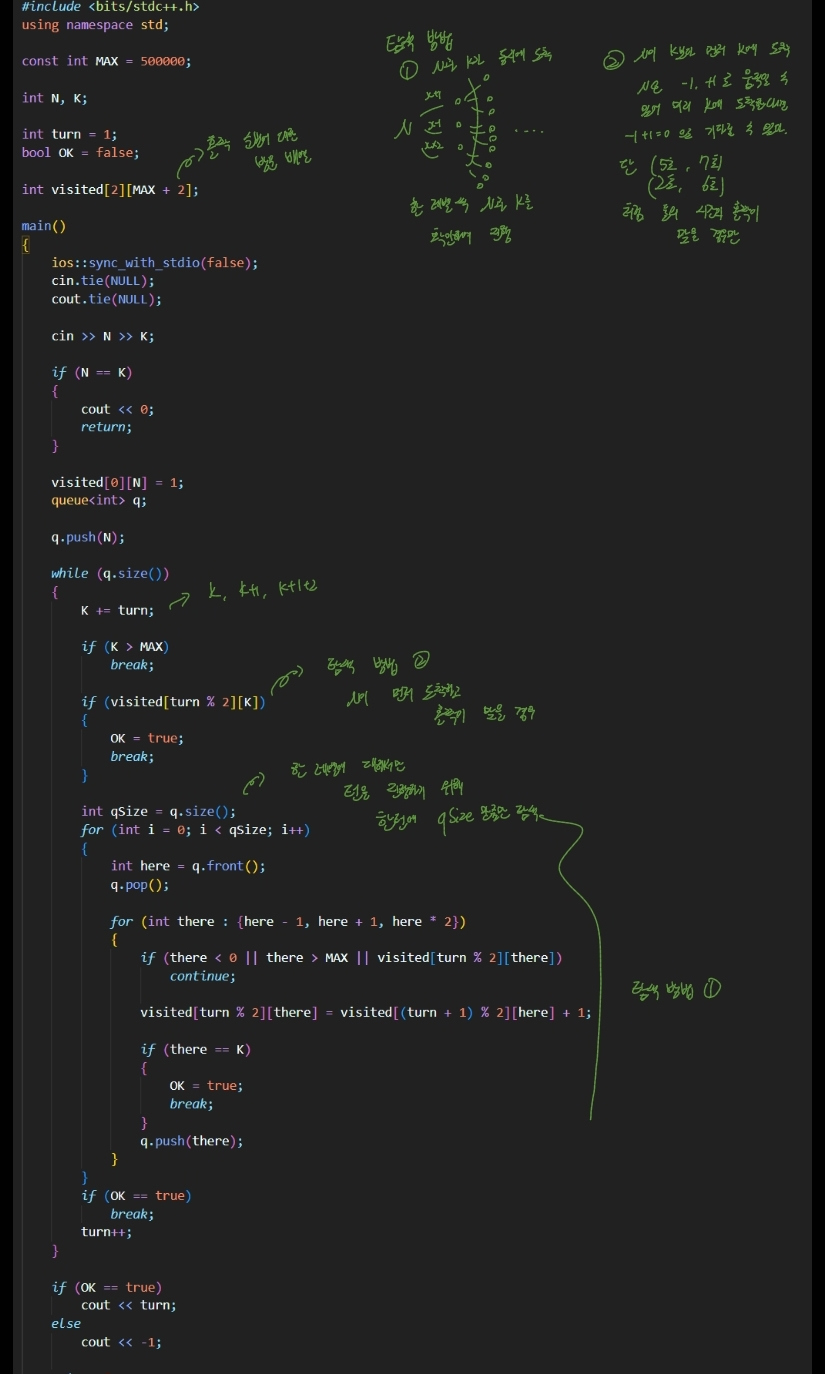
풀이와 코드
탐색 방법은 크게 두 가지로
- N 이 K 를 같은 턴에 만나는 경우
- N 이 K 에 먼저 도착해서 기다리는 경우
1번은 기존의 BFS 탐색처럼 N 이 가능한 진행 방법 (N - 1, N + 1, N * 2) 으로 이동하고
K 또한 턴 진행에 따라 커지면서 같은 장소에 만나는 것이다.
2번은 N 이 먼저 도착하는 것인데 이 방법이 가능한 이유는 N 의 이동이 -1, +1 로 가능하여
만약 먼저 K 에 도착한다면 -1, + 1 을 반복하여 기다리는 것이 가능하다.
따라서 visited 배열에서 K 위치가 채워졌는지를 확인하면 되는데 이때 주의할 점은
-1, +1 로 N 이 먼저 도착해서 기다리는 경우는 두 개의 턴이 같은 홀수와 짝수일 때이다.
예를 들어 N 이 5초에 도착한다면 K 역시 같은 홀수인 7초에 도착한 경우만 N 이 기다리고 있다고
판단할 수 있다. 만약 K 가 6초에 도착한다면 N 과 K는 만났다고 할 수 없다.
그러므로 홀수번째 도착과 짝수번째 도착을 구분하기 위해 visited 배열을 2차원으로 선언하여
탐색을 진행하게 된다.
리뷰
이 숨바꼭질 시리즈를 계속 연속으로 풀고 있는데 문제마다 그래프 탐색을 위한 조건과 방식이
달라서 가장 기본적인 BFS 탐색 구현 이외로는 전부 다 막혔었다.
BFS 코테 준비를 위해 꼭 숨바꼭질 시리즈를 복습하자!