문제
N2개의 동전이 N행 N열을 이루어 탁자 위에 놓여 있다. 그 중 일부는 앞면(H)이 위를 향하도록 놓여 있고, 나머지는 뒷면(T)이 위를 향하도록 놓여 있다. <그림 1>은 N이 3일 때의 예이다.
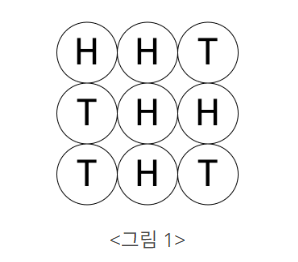
이들 N2개의 동전에 대하여 임의의 한 행 또는 한 열에 놓인 N개의 동전을 모두 뒤집는 작업을 수행할 수 있다. 예를 들어 <그림 1>의 상태에서 첫 번째 열에 놓인 동전을 모두 뒤집으면 <그림 2>와 같이 되고, <그림 2>의 상태에서 첫 번째 행에 놓인 동전을 모두 뒤집으면 <그림 3>과 같이 된다.

<그림 3>의 상태에서 뒷면이 위를 향하여 놓인 동전의 개수는 두 개이다. <그림 1>의 상태에서 이와 같이 한 행 또는 한 열에 놓인 N개의 동전을 모두 뒤집는 작업을 계속 수행할 때 뒷면이 위를 향하도록 놓인 동전의 개수를 2개보다 작게 만들 수는 없다.
N2개의 동전들의 초기 상태가 주어질 때, 한 행 또는 한 열에 놓인 N개의 동전을 모두 뒤집는 작업들을 수행하여 뒷면이 위를 향하는 동전 개수를 최소로 하려 한다. 이때의 최소 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 20이하의 자연수 N이 주어진다. 둘째 줄부터 N줄에 걸쳐 N개씩 동전들의 초기 상태가 주어진다. 각 줄에는 한 행에 놓인 N개의 동전의 상태가 왼쪽부터 차례대로 주어지는데, 앞면이 위를 향하도록 놓인 경우 H, 뒷면이 위를 향하도록 놓인 경우 T로 표시되며 이들 사이에 공백은 없다.
출력
첫째 줄에 한 행 또는 한 열에 놓인 N개의 동전을 모두 뒤집는 작업들을 수행하여 뒷면이 위를 향하여 놓일 수 있는 동전의 최소 개수를 출력한다.
풀이와 코드
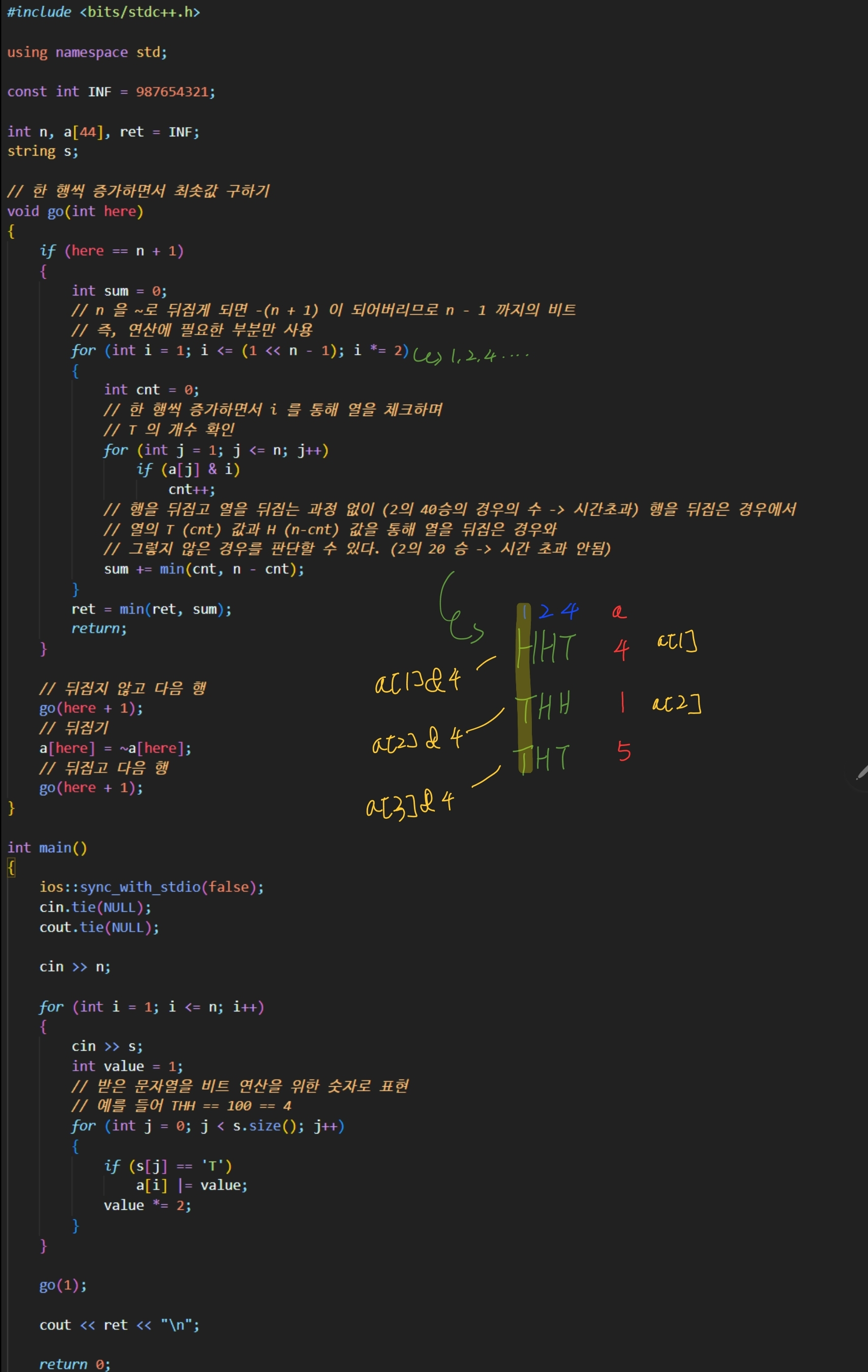
모든 행과 열을 뒤집는 경우의 수를 생각해본다면 2의 40승으로 시간초과가 발생한다.
따라서 이를 방지하기 위해서는 다른 접근이 필요한데
만약 행을 모두 바꾸는 경우에서 열을 확인하면서 T 의 개수를 세고
H 의 개수를 센다면 열을 뒤집지 않고도 열이 뒤집힌 경우와 뒤집히지 않은 경우를
만들 수 있어 경우의 수는 2의 20승 까지 줄일 수 있다.
리뷰
거의 처음 접한 비트 마스킹 문제로 문제를 이해하고 막혀서 정답을 이해하고
문제의 접근 방식을 정리해보았다.
문자열을 비트 마스킹의 연산으로 변환하는 부분부터 행을 뒤집거나 뒤집지 않으면서
열을 체크하는 방식의 동작 과정이 이해는 되었으나 스스로 적용하는데는 아직 부족하니
이 문제는 비트 마스킹을 복습할 때 꼭 한번씩 확인해보자!!