📌 통계학(statistics)
기술통계학(descriptive statistics)
데이터를 수집하고 수집된 데이터를 쉽게 이해하고 설명할 수 있도록 정리 요약 설명하는 방법론
추론통계학(inferential statistics)
모집단으로부터 추출한 표본 데이터를 분석하여 모집단의 여러가지 특성을 추측하는 방법론
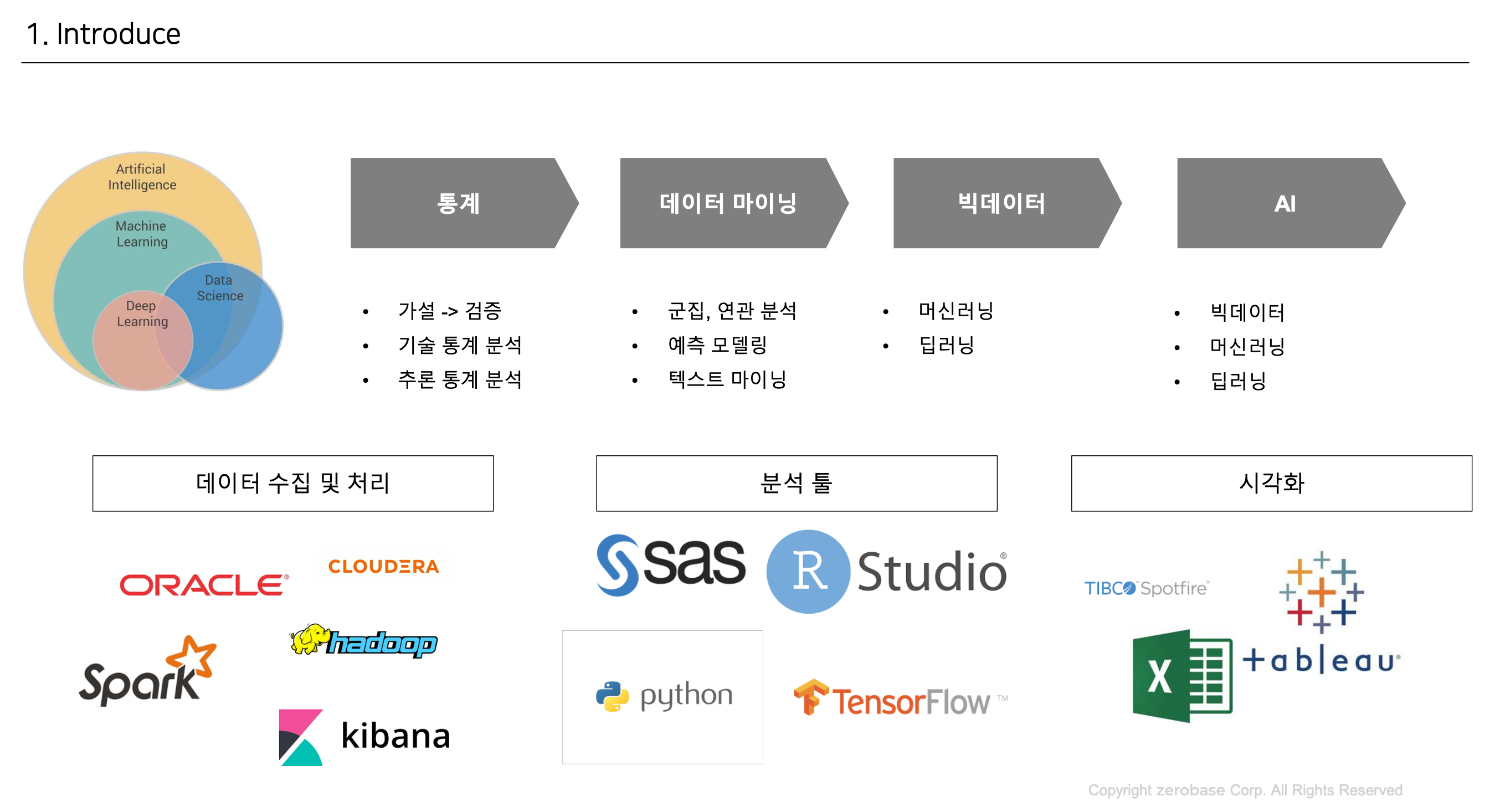
📌 데이터의 이해
데이터와 그래프
- 변수 (Variable)
- 질적 자료 - 명목형 변수, 순서형 변수
- 양적 자료 - 이산형 변수, 연속형 변수
- 데이터 시각화 (Data Visualization)
EDA: Exploratory Data Analysis
1. 데이터 분석 프로젝트 초기에 가설을 수립하기 위해 사용
2. 데이터 분석 프로젝트 초기에 적절한 모델 및 기법의 선정
3. 변수 간 트렌트, 패턴, 관계 등을 찾고 통계적 추론을 기반으로 가정을 평가
4. 분석 데이터에 적절한가 평가, 추가 수집, 이상치 발견 등에 활용
데이터의 기초 통계량
- 기초 통계량
- 중심 경향치:
평균,중앙값(median),최빈값(mode),절사 평균- 산포도:
범위(range),사분위수(quartile),분산(variance),표준편차(standard deviation),변동 계수(Coefficient of Variation: CV)
- 사분위수(quartile)
IQR(interquartile range, 사분위수 범위): Q3 - Q1 - 왜도(skew), 첨도(kurtosis)
📌 확률 이론 - 확률
- 확률 (probability)
- 표본 공간 (Sample Space)
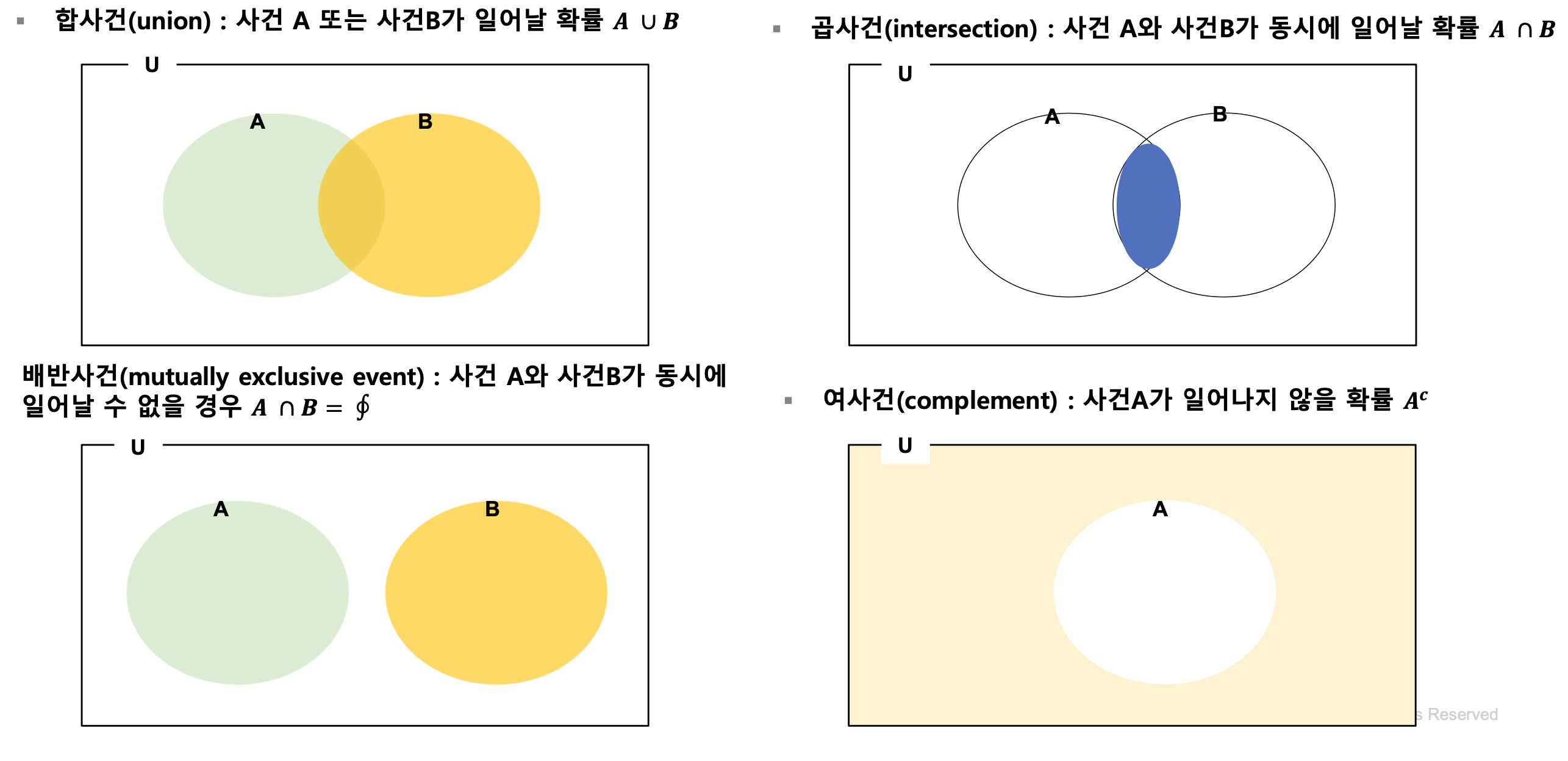
확률의 성질
- 합사건(union), 곱사건(intersection), 배반사건(mutually exclusive event), 여사건(complement)
조합과 순열
- ! (Factorial)
- 순열 (Permutation)
- 조합 (Combination)
- 조건부확률 (conditional probability)
- 확률의 곱셈법칙
- 베이즈 정리 (Bayes' Theorem)
📌 확률 이론 - 확률변수
확률 변수 (random variable)
- 확률 변수: X, Y 등 대문자로 표현
- 확률 변수의 특정값: x, y 등 소문자로 표현
- 이산 확률 변수 (discrete random variable)
- 연속 확률 변수 (contiuous random variable)
확률 변수의 평균: 기대값, E(X)
- 공분산: 2개의 확률변수의 선형 관계를 나타내는 값.
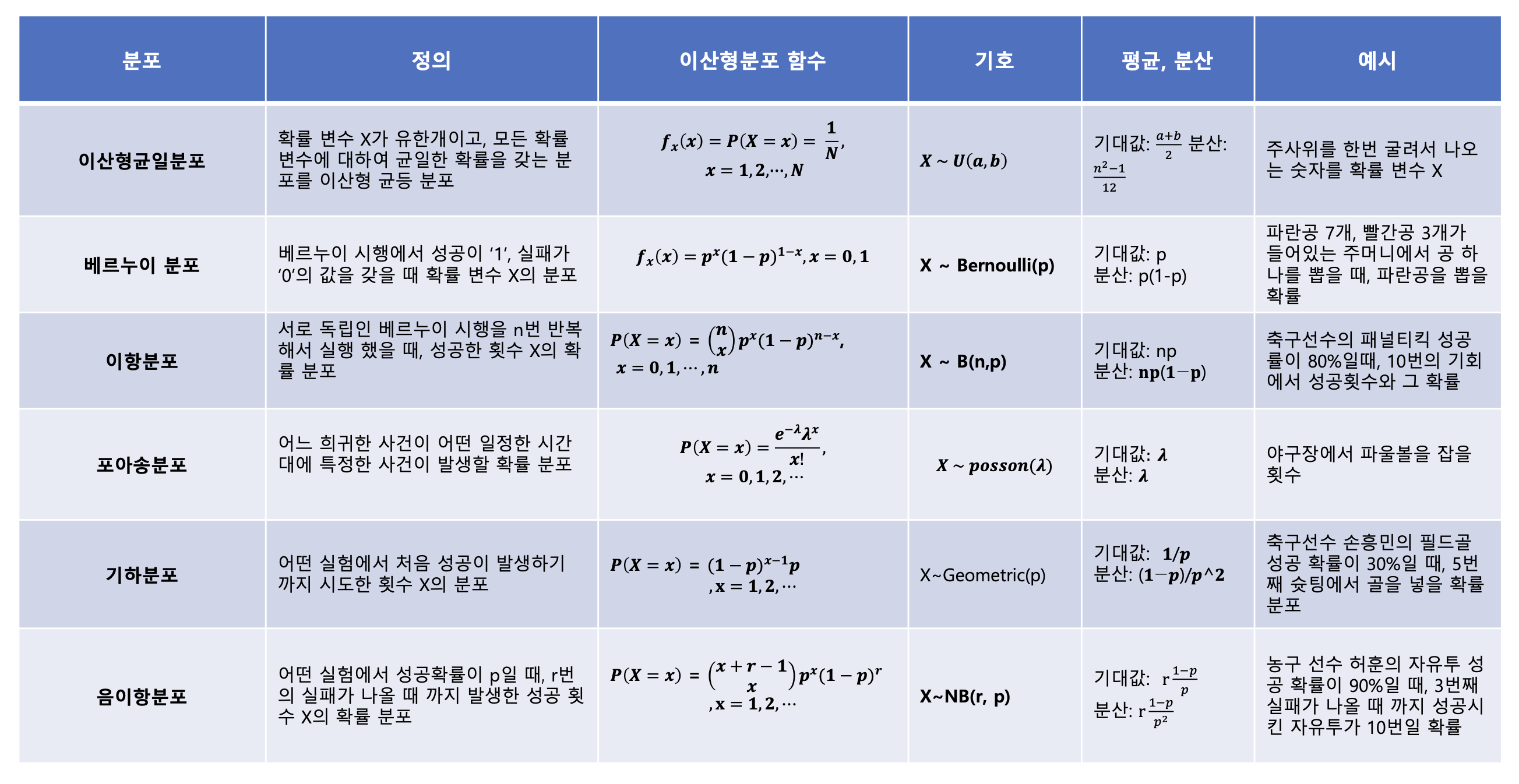
📌 이산형 확률 분포
확률 분포 (probability distribution): 확률 변수 X가 취할 수 있는 모든 값과 그 값을 나타낼 확률을 표현한 함수
- 이산형 확률분포, 연속형 확률분포