✅ 점화식
내 아이디어는 아래와 같다.
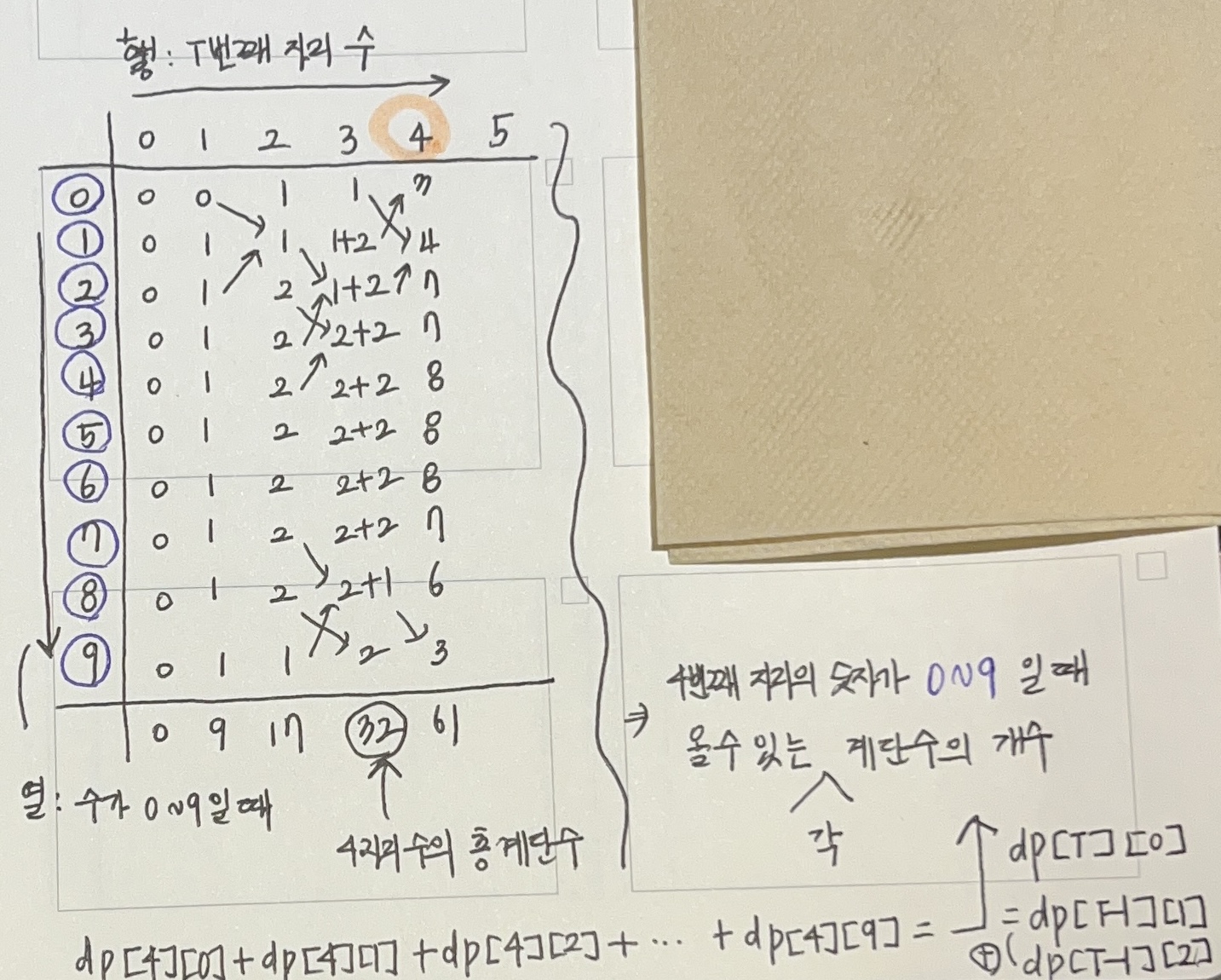
i번째 자리가 0-9까지 가능하니까 그 자리의 왼쪽으로 탐색하면서 경우의 수를 더해주는 거다.
그러면 점화식이 대략
dp[4][0] = dp[3][1]
dp[4][1] = dp[3][0] + dp[3][2]
dp[4][2] = dp[3][1] + dp[3][3]이런식으로 가니까
dp [ jarisu ][ j] = do [ jarisu-1 ][ j ] + dp [ jarisu-1 ][ j ]이렇게 되고 j의 구간은 0 <= j <= 0 일 것 이다!
뭔가 배열 하나로도 할 수 있을 것 같기도 한데.. 아닌가..음 하나로 하면 복잡할 것 같긴한데.. 따로 배열을 하나 더 만들면 될 것 같기도 하고..
이전 이친수 문제에서 좀 더 변형된 문제이다.
mod 아이디어는 참고를 좀 했고, 이친수를 풀고 난 다음에 바로 문제를 풀었다.
그래도 약 한 시간 안으로 아이디어 + 구현을 마무리 할 수 있었던 문제였다.
✅ 맞왜틀 코드
long으로 배열 선언해줬는데 맞왜틀..!
import java.util.Scanner;
public class Main {
static long[][] dp;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
dp = new long[n + 1][10];
dp[0][0] = 0;
dp[1][0] = 0;
for (int j = 1; j <= 9; j++) {
dp[0][j] = 0;
dp[1][j] = 1;
}
for (int i = 2; i <= n; i++) {
dp[i][0] = dp[i - 1][1];
dp[i][9] = dp[i - 1][8];
for (int j = 1; j <= 8; j++) {
dp[i][j] = dp[i - 1][j - 1] + dp[i - 1][j + 1];
}
}
long result = 0;
for (int j = 0; j <= 9; j++) {
result += dp[n][j] % 1000000000;
}
System.out.println(result);
}
}
✅ 코드
위에 배열에서도 엄청 큰 수가 나오고
밑에 result에서도 엄청 큰 수가 나오는구나.
그래서 둘 다 mod를 해줘야 한다.
또한! result += dp[n][j] % 1000000000 하면 니눗셈이 먼저 실행되므로 아래처럼 식을 써줘야 한다.
result = (result+dp[n][j]) % 1000000000;import java.util.Scanner;
public class Main {
static long[][] dp;
static long mod = 1000000000;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
dp = new long[n + 1][10];
dp[0][0] = 0;
dp[1][0] = 0;
for (int j = 1; j <= 9; j++) {
dp[0][j] = 0;
dp[1][j] = 1;
}
for (int i = 2; i <= n; i++) {
dp[i][0] = dp[i - 1][1];
dp[i][9] = dp[i - 1][8];
for (int j = 1; j <= 8; j++) {
dp[i][j] = (dp[i - 1][j - 1] + dp[i - 1][j + 1]) % mod;
}
}
long result = 0;
for (int j = 0; j <= 9; j++) {
result = result + dp[n][j] % mod;
}
System.out.println(result);
}
}