
재귀(Recursion)란?
재귀란, 어떠한 것을 정의할 때 자기 자신을 참조하는 것이다.
즉, 자신이 자신을 호출하는 것이다.
def recursive():
print("Recursive call!\n")
recursive() # 자기 자신을 호출한다.위 코드의 recursive 함수는, 함수 내부에서 자신을 호출하고 있다.
이러한 함수를 재귀 함수라고 한다.
위 함수를 실행하면, 아래의 이미지와 같이 동작한다.
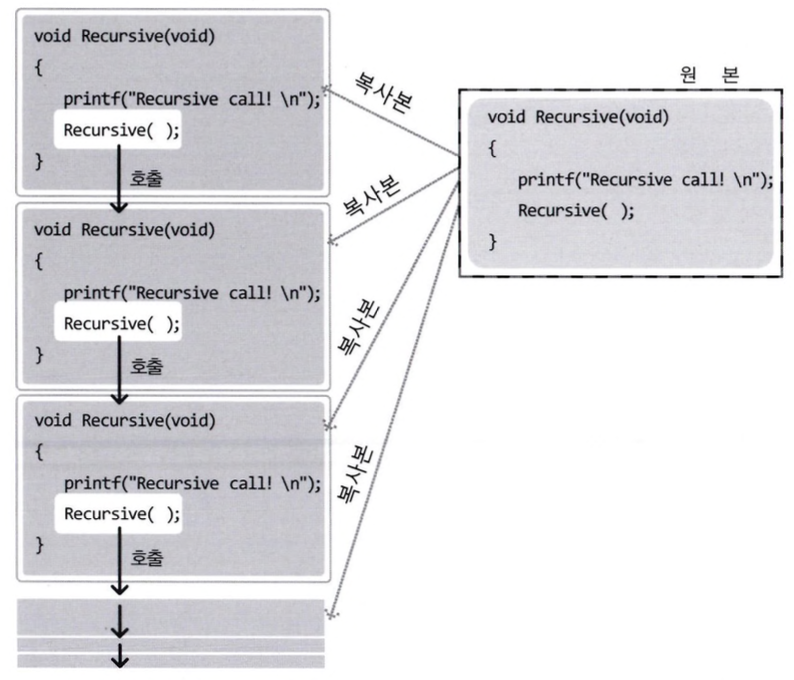
recursive 함수가 호출되면, 이 함수의 복사본이 만들어져 복사본이 실행되는 구조이다.
위 함수에는 치명적인 문제점이 존재한다. 문제점은 바로 함수가 끊임없이 호출된다는 것이다.
재귀 함수 내부에는 꼭
재귀의 탈출조건이 있어야 한다.
그렇다면 위의 함수에 재귀의 탈출조건을 추가해보자.
def recursive(num):
if num <= 0:
return # 재귀의 탈출조건
print(f"Recursive call! {num} \n")
recursive(num - 1) # 자기 자신을 호출한다.재귀의 활용
재귀를 활용하는 몇 가지 예시들을 통해, 재귀함수를 잘 정의하는 연습을 해보자.
1. 피보나치 수열 (Fibonacci Sequence)
피보나치 수열은 재귀적인 형태를 띠는 대표적인 수열로,
앞의 값 2개를 더하여 현재의 수를 만드는 수열이다.
(1, 2번째 값은 제외)
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, ...즉, 수열의 n번째 값은 수열의 n-1번째 값과 n-2번째 값을 합한 값이다.
이를 코드로 풀어보면 아래와 같다.
def fibonacci(n): # 피보나치 수열의 n번째 값 반환하는 함수
if n == 1:
return 0
elif n == 2:
return 1
else:
return fibonacci(n-1) + fibonacci(n-2)2. 이진 탐색 알고리즘의 재귀적 구현
이진 탐색 알고리즘은 앞서 정렬되어 있는 리스트에서 탐색 범위를 절반씩 좁혀가며 데이터를 탐색하는 알고리즘이라고 설명했었다.
탐색 범위를 좁히는 과정은 매 단계가 동일하기 때문에, 재귀적으로 구현할 수 있다.
이진 탐색 알고리즘의 반복 패턴을 정리해보면 아래와 같다.
- 탐색 범위의 중앙에 목표 값이 저장되었는지 확인한다.
- 저장되지 않았다면 탐색 범위를 반으로 줄여서 다시 탐색한다.
탐색이 실패하는 경우는 first(탐색범위의 시작)가 last(탐색범위의 끝)보다 커지는 경우이다.
위 내용을 코드로 풀어보면 아래와 같다.
def binary_search(ar, first, last, target):
# first 값이 last 값보다 크다면 탐색 실패
if first > last:
return -1
# first <= last인 경우 계속 탐색
mid = (first + last) // 2
# 중앙값이 target과 같다면 탐색 성공
if ar[mid] == target:
return mid
elif ar[mid] > target:
return binary_search(ar, first, mid - 1, target)
else:
return binary_search(ar, mid + 1, last, target)3. 하노이 타워
하노이 타워 문제는 재귀함수를 사용하는 아주 아주 대표적인 예시로 손꼽히는 문제이다.
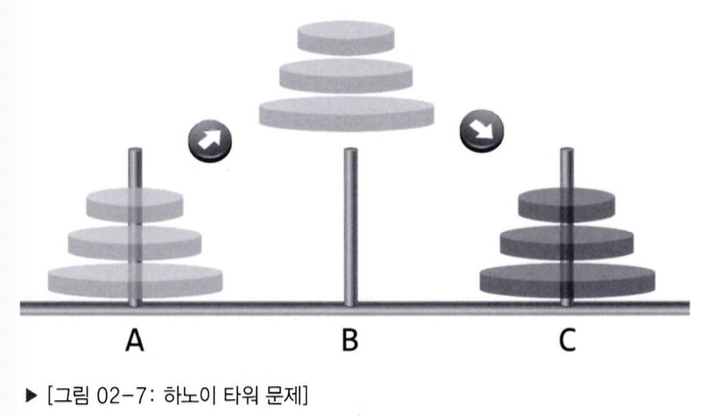
- 하나의 막대에 쌓여 있는 원반을 다른 하나의 원반에 그대로 옮기는 방법을 찾는 문제이다.
- 원반은 한 번에 하나씩만 옮길 수 있다.
- 옮기는 과정에서, 작은 원반의 위에 큰 원반이 올려져서는 안 된다.
막대 A에 있는 모든 원반을 막대 C로, 동일한 형태로 옮겨야 한다.
원반의 크기가 작은 것부터 1, 2, 3번이라고 하자.
이 문제의 해결 방법을 천천히 따라가보면,
- C 막대에 가장 처음 3번을 놓아야 하는데 위에 얹어진 1, 2번 원반 때문에 옮길 수 없다.
- 즉, 1번과 2번 원반을 B에 놓으면 3번 원반을 C에 놓을 수 있다.
위 논리에 의하면,
세 개의 원반을 막대 C에 옮기기 위해서는,
1, 2번 원반을 막대 B에 옮기는 문제부터 해결해야 한다.
그렇다면, 원반이 4개인 경우엔 어떻게 될까?
원반의 크기가 작은 것부터 1, 2, 3, 4번이라고 한다면,
- C 막대에 가장 처음 4번을 놓아야 하는데 위에 얹어진 1~3번 원반 때문에 옮길 수 없다.
- 즉, 1번, 2번, 3번 원반을 B에 놓으면 4번 원반을 C에 놓을 수 있다.
1, 2, 3번 원반을 막대 B에 옮긴 후 4번 막대부터 C로 옮긴다.
이를 일반화하면,
- 작은 원반 n - 1개를 A에서 B로 이동한다.
- 큰 원반(가장 아래의 원반)을 A에서 C로 이동한다.
- 작은 원반 n - 1개를 B에서 C로 이동한다.
로 정리할 수 있다.
위 내용을 코드로 풀어보면 아래와 같다.
# start에 꽂혀있는 num개의 원반을 by를 거쳐 end로 이동시키는 함수
def hanoi_tower(num, start, by, end):
if num == 1:
print(f"원반1을 {start}에서 {end}로 이동 \n")
else:
hanoi_tower(num - 1, start, end, by) # n-1 개의 원반을 A에서 B로
print(f"원반{num}을 {start}에서 {end}로 이동")
hanoi_tower(num - 1, by, start, end)