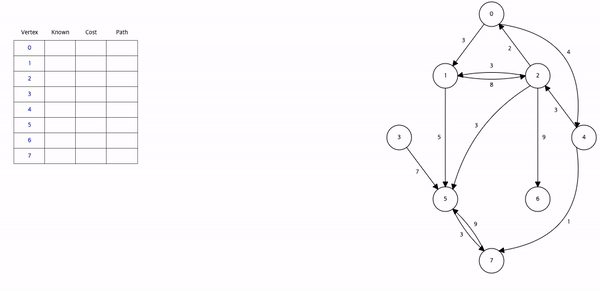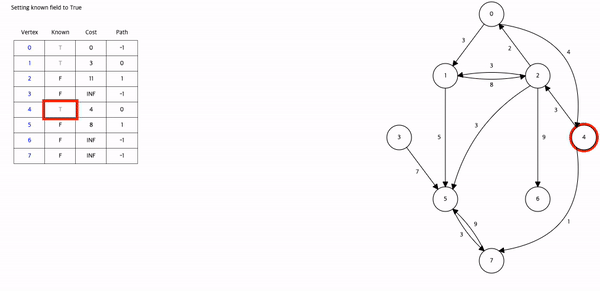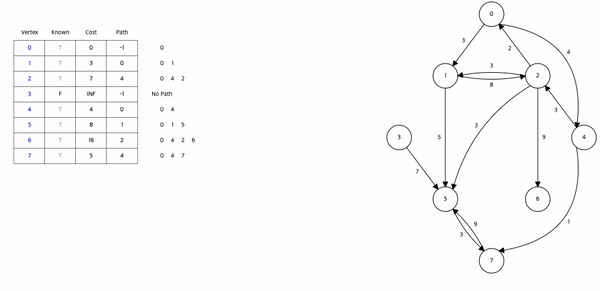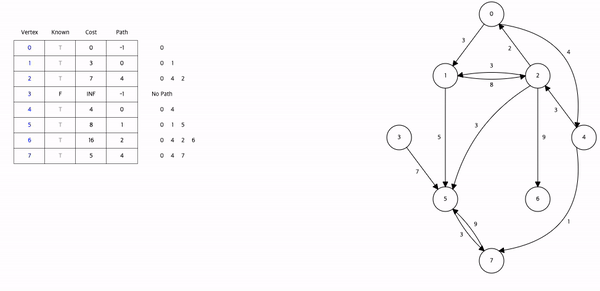
하나의 시작 정점 v에서 다른 모든 정점까지의 최단경로를 찾는 알고리즘.
시간 복잡도 : O(n^2)
모든 정점에서 출발해야 한다면 시간복잡도는 O(n^3)
(Floyd 알고리즘의 시간복잡도 O(n^3))
-> Floyd는 3중 for문으로 간결하게 써서 편함.
- 시작정점 v : 최단경로탐색의 시작 정점.
- 집합 S : 시작 정점 v 로부터 최단경로가 이미 발견된 정점들의 집합.
- dist 배열 : S에 있는 정점만을 거쳐서 다른 정점으로 가는 최단거리를 기록하는 배열. (프림의 MST 알고리즘에서와 유사) dist[v] = 0 (시작정점)
만약 그래프의 모든 정점 u 에 대해 시작 정점 v 와의 간선 (u,v) 가 있으면, dist[u] 는 weight[v][u], 즉 간선 (u,v) 의 가중치로 초기화 된다. 만약 간선이 없으면 dist[u] 는 무한대 값으로 초기화 된다.
시작 단계에서는 아직 최단경로가 발견된 정점이 없으므로 S = {v} 이다. 즉 처음에는 시작 정점 v를 제외하고는 최단거리가 알려진 정점이 없다. 알고리즘의 기본 아이디어는 매 단계에서 S 안에 있지 않은 정점들 중에서 가장 dist 값이 작은 정점을 S에 추가하는 것이다.