알고리즘
1.다익스트라 최단경로 알고리즘
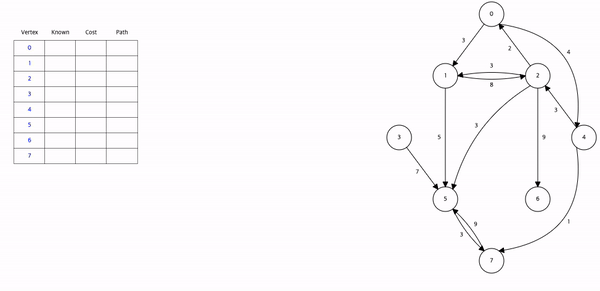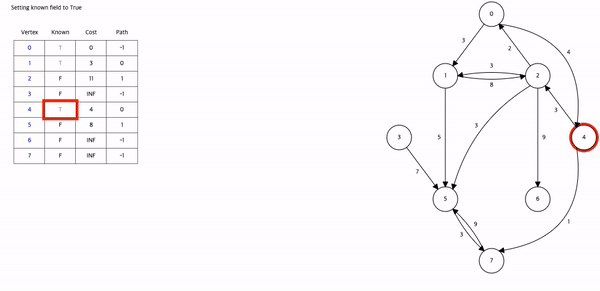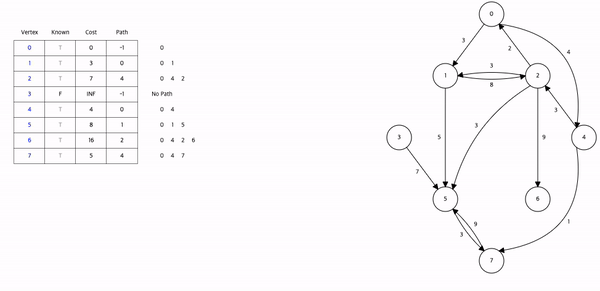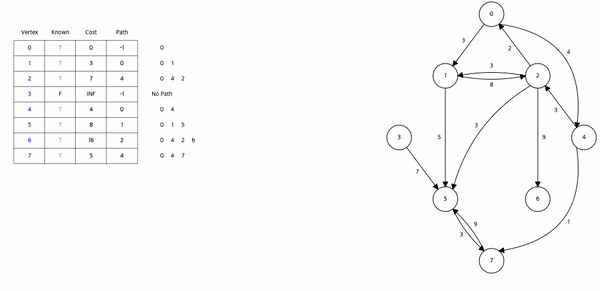
시간 복잡도 : O(n^2)모든 정점에서 출발해야 한다면 시간복잡도는 O(n^3)(Floyd 알고리즘의 시간복잡도 O(n^3))\-> Floyd는 3중 for문으로 간결하게 써서 편함.시작정점 v : 최단경로탐색의 시작 정점.집합 S : 시작 정점 v 로부터 최단경로가
2.위키 - 이진검색 알고리즘

이진 검색 알고리즘(binary search algorithm)은 오름차순으로 정렬된 리스트에서 특정한 값의 위치를 찾는 알고리즘이다. 처음 중간의 값을 임의의 값으로 선택하여, 그 값과 찾고자 하는 값의 크고 작음을 비교하는 방식을 채택하고 있다. 처음 선택한 중앙값
3.트리

계층적인 자료의 표현에 적합한 자료구조.컴퓨터에서도 트리는 다양한 응용을 갖는다. 폴더구조를 표현하는 것은 물론이고, 효율적인 탐색을 위한 탐색트리, 우선순위 큐를 위한 힙 트리, 인공지능 문제에서 의사결정 구조를 표현하기 위한 결정 트리 등 매우 광범위하게 활용된다.
4.이진트리의 종류와 성질.

높이 k의 이진트리의 노드의 수 :2^(1-1) + 2^(2-1) + . . . + 2^(k-1) = 2^k - 1 힙(heap) 은 완전이진트리의 대표적인 예이다.성질 : n개의 노드를 가진 트리는 n-1개의 edge를 갖는다.표현법 : 배열 표현법, 링크 표현법.트
5.validAnagram 문제풀이
내 풀이 일단 간단하게 풀어봤다. Array.prototype.map
6.sumZero 문제풀이

해설더해서 0이 나와야됨.가장 먼저 0이 된 값들을 리턴해야 되므로, 투 포인터 문제라고 생각이듦. \-> 투 포인터가 각각 0미만 0초과여야 한다. \-> 두 값의 합이 0이면 바로 리턴 \-> 아니라면 idx 를 하나씩 줄임. \-> arridx의 절대값이
7.countUniqueValues 문제풀이

내 풀이집합으로 풀기.투포인터로 풀기.둘다 O(N)으로 나쁘지않다.집합으로 푸는 방법을 처음에 생각했는데, 쉽지만 알고리즘적인 풀이가 아닌 것 같다.하지만, 간단하게 풀리니까 Set을 잘이용하면 괜찮을 것 같다.참고로 Set 연산의 시간 복잡도는 다음과 같을 것이다.n
8.maxSubArray 문제풀이

설명아이디어가 안떠올라서 일단 O(N^2)으로 풀었다.풀이방식은 이중 for문을 이용해서 모든 합을 비교하여 가장 큰 값을 찾았다.처음에 for문 한번만 써서 풀고싶었기에, idx를 갱신해주면서 풀이하려고 했다.이렇게 풀게되면, if 문에 걸리지않았을 때 연속된 수열이
9.Sliding Window 알고리즘

일정한 범위를 가지고 있는 것을 유지하면서 이동하는 것.
10.Divide and Conquer 알고리즘

주로 배열이나 문자열 같은 큰 규모의 데이터셋을 처리한다.분할정복은 시간복잡도를 어마어마하게 줄여줄 수 있다.값을 찾기 위해 왼쪽에서 오른쪽 끝까지 이동하기보다는,작은 조각으로 세분하여 각 조각들을 어디로 이동시킬지 결정하는 작업search.js내 풀이설명옛 기억을 최
11.sameFrequency 문제풀이

내 풀이조금 더 좋은 방법이 있을 것 같긴 한데, 일단 O(N)으로 풀었다.
12.areThereDuplicates 문제풀이

2가지 방법으로 문제를 풀었다.
13.averagePair 문제풀이

투 포인터로 해결while문 돌면서 크기 비교후 start, end값 결정다돌았는데 return 안됐을 때 false return시간복잡도: O(N)공간복잡도: O(1)
14.isSubsequence 문제풀이

인덱스를 움직이며 풀었다.while문 탈출시에 idxA가 a.length와 같다면 모든 단어를 포함했다는 뜻 -> true아니라면 false재귀로 풀 수도 있다.비교시에 값이 \- 같을 때: return isSubsequence(a.slice(1), b.slice(1