요약
- imbalanced되어있으면서도, ranking이 중요한 데이터에 대해서(e.g. click이 잘 일어나지 않지만, ctr의 순위를 잘 결정하는것이 중요한 데이터에 대해서) 평가 지표를 찾는다.
- accuracy, f1score, ROC AUC, PR AUC 등의 여러 지표를 탐구함.
- 결론
- 일반적으로 imbalanced data 는 f1-score, pr auc 등의 지표를 쓰는게 좋다고 하지만, 지속적 모니터링을 위해서는 기준점이 명확한 것이 좋다는 점이 있었음(아래 상세 기술) 이런 이유로 이 지표들보다는 데이터의 balance를 맞춰준 후, roc auc 를 적용하는게 더 옳다고 판단함.
- pr auc vs roc auc
- pr auc
- imbalanced data 에서 성능평가를 할때에 유용함
- recall 의 어느 시점에 precision 이 빠르게 떨어지기 시작하는지를 파악해서 threshold 지정
- 단, 데이터에 따라서 기준 score 가 변화함(random 분류의 경우 기댓값은 positive:negative=1:k 일때 1/(1+k)가 됨)
- roc auc
- imbalanced data 에 취약함
- 기준 score 변화가 전혀 없음(random 분류의 경우 데이터에 상관없이 score 값은 0.5)
- pr auc
Evaluation metric recap
1. Accuracy
-
imbalanced 된 상태에서는 절대 써선 안된다
-
대부분을 majority class로 분류해버리는 경우 accuracy 가 높게 측정될 수 있음
-
beta >1 이면 커질수록 optimal threshold는 점점 낮아진다.

-
class 단위로 구분돼있을때 사용할 수 있는 지표라서, softlabel로 존재하는 경우 threshold 를 정하기 위해 위에서와 같은 차트를 그려볼 수도 있다.
-
언제 사용?
- balanced 돼 있을때
- non-technical stakeholder 에게 설명할때
- 모든 class 가 중요할때
2. F1 score
-
precision, recall 을 조화평균한 것
-
recall 이 더 중요할 수록 beta 값을 올려야
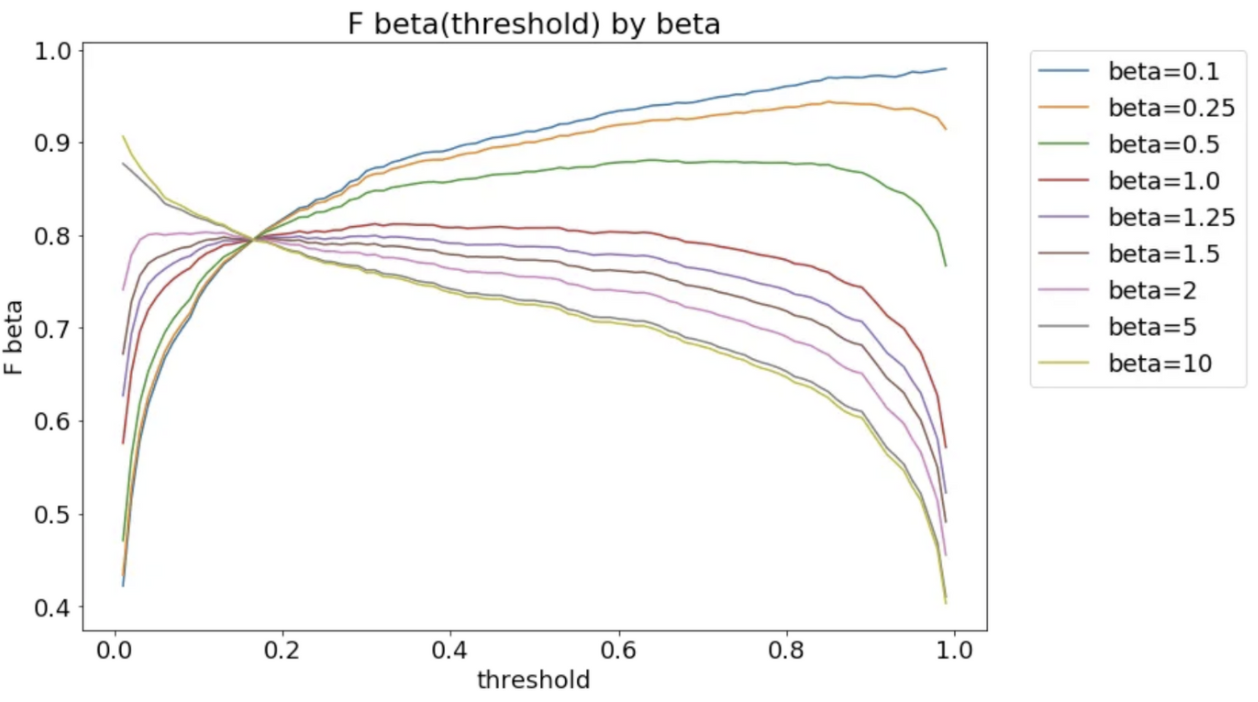
-
0<beta<1이면 precision 을 더 중시하는 것 → threshold 가 높을수록 f-beta score 도 올라감
-
beta >1 이면 커질수록 optimal threshold는 점점 낮아진다.
-
class 단위로 구분돼있을때 사용할 수 있는 지표라서, softlabel로 존재하는 경우 threshold 를 정하기 위해 위에서와 같은 차트를 그려볼 수도 있다.
-
언제쓰나
- positive class 에 대해서 더 신경쓸때 많이 씀
- easily explained to business stakeholders
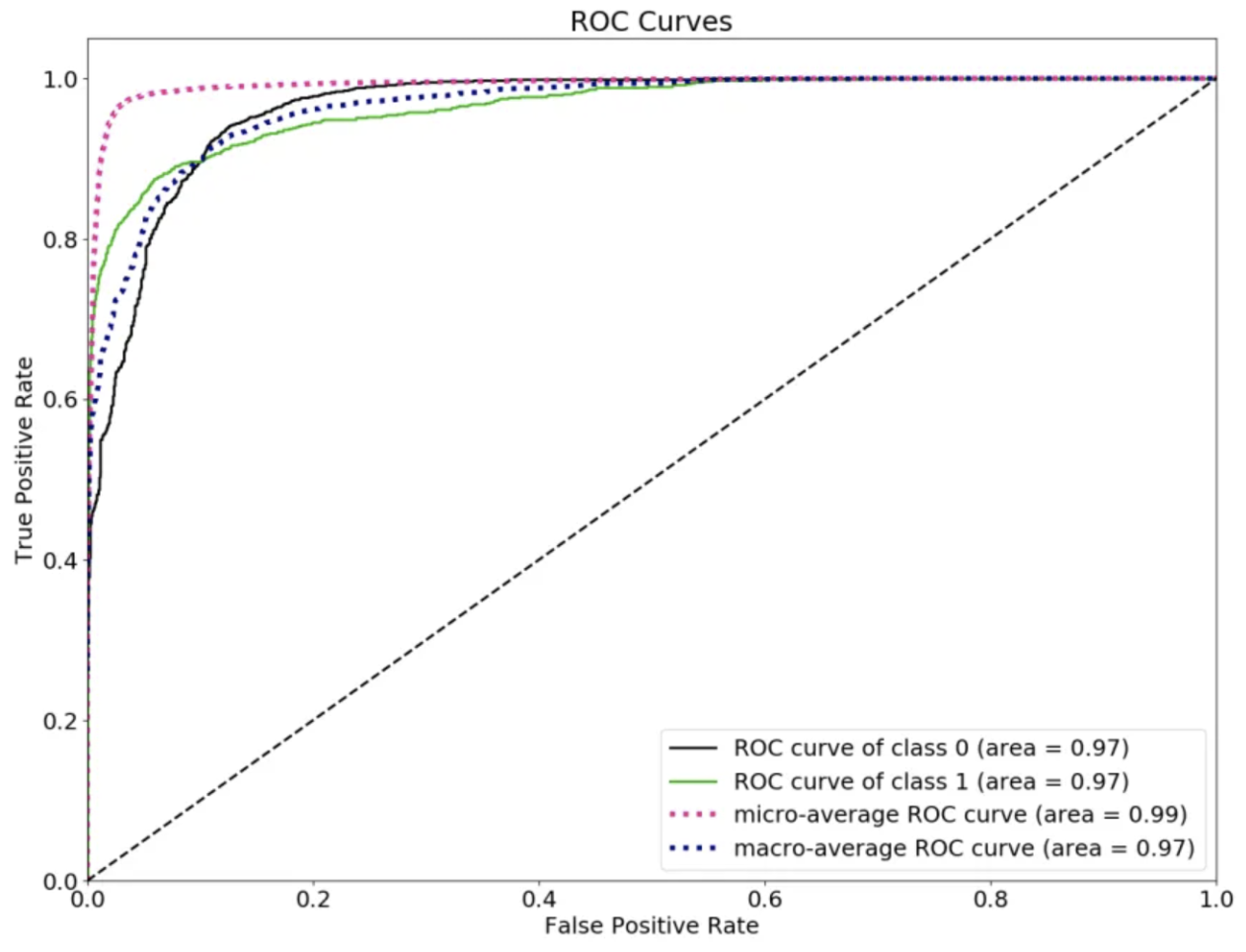
3. ROC AUC
- (Receiver Operating Characteristics)
- True positive rate(x축) 와 false positive rate(y축) 사이의 tradeoff 를 visualize 함
- ranking 에 대해 focus
- prediction 과 target 의 rank 사이의 상관관계와 동치 → 해당 모델의 ranking prediction 이 얼마나 좋은지를 측정
- 임의로 고른 positive instance 가 임의로 고른 negative instance 보다 score 가 낮은지를 확인
- 기준값이 명확
- 랜덤상황을 가정하면 그 socre 값이 positive negative 와 상관없이 정확히 0.5가 된다.
- 0.5 : 랜덤 (전체집합에서 positive negative 와 상관없이)
- 0.7~ : 괜찮은 모델이라 판단 가능
- 언제쓰나?
- 정확한 확률값에 대한 것 보다 ranking 에 대한 prediction 을 할때에 사용해야함
- 데이터가 심하게 imbalanced 되어있으면 사용해선 안된다.
- true negative 가 많아서 false positive rate 가 내려갈 수도 있기 때문
- positive negative 둘 다에 대해서 동일하게 중요하게 생각할때 사용
- 만약 true negative 만큼 true positive 가 중요하면 roc auc 를 쓰는게 말이 된다.
4. PR AUC(=Average Precision)
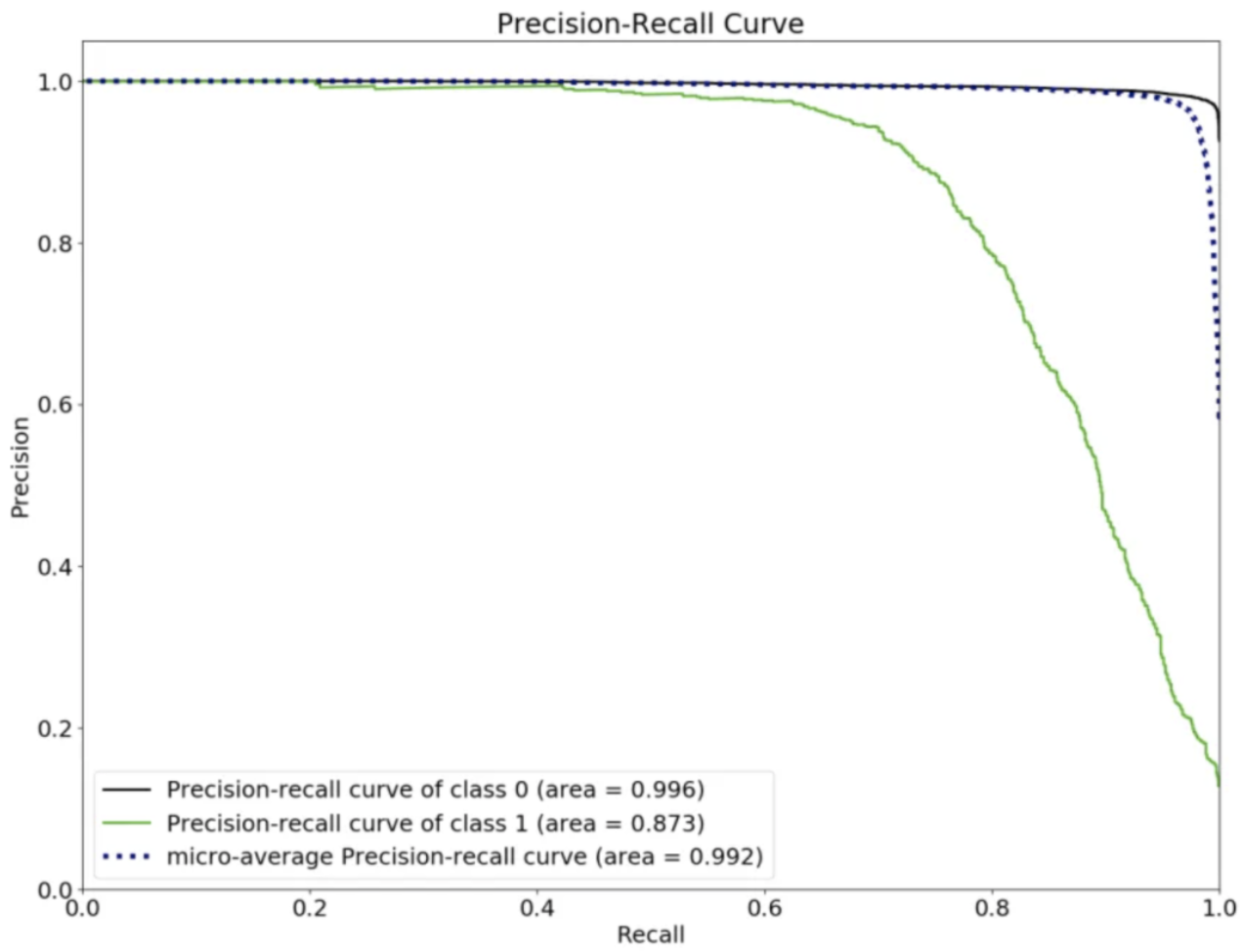
- precision 과 recall 을 한방에 그리는 것
- recall 의 변화에 따른 precision 들을 다 모아서 평균을 낸다.
- y 축 값이 높을수록 좋은 모델인 것
- recall 의 어느 시점에서 precision 이 빠르게 떨어지기 시작하는지를 파악해서 threshold 를 정해야함
- recall 에 따른 평균이기때문에 랜덤하게 pick 했을때의 기댓값은 0.5가 아니고 초기 p:n=1:k 라고 할 때 1/(1+k) 가 됨. → threshold 이동하면서 그린 그림에서는 true label 안에서 p 와 n의 비율이 계속해서 변하기때문에 random 과의 관계를 표현할 수 있다면 괜찮지만, 그렇지 않다면 값 자체를 신뢰하기는 어려워질 수 있음
- 언제쓰나
- 설득용
- business 에 맞는 threshold 찾고자 할때
- 데이터가 매우 imbalanced 되어있을 때
- positive class가 negative class 에 비해서 더 중요할 때
- pr auc 는 주로 positive class 에 주목하게 되므로, frequent negative class 에 대해서는 무시하게 되는 경향이 크다.(https://www.ncbi.nlm.nih.gov/pmc/articles/PMC4349800/)
5. others
- micro macro
- micro : 평균을 계산할때 각 클래스의 샘플 수를 고려해서 평균을 취함(이전에 내가 balancing 을 한 것과 동일한 듯)
- 클래스 불균형 등에 민감하게 반응 가능
- macro : 각 클래스의 샘플 수에 상관 없이 평균 취함
- 모델의 전반적인 성능에 대해 평가 가능
- micro : 평균을 계산할때 각 클래스의 샘플 수를 고려해서 평균을 취함(이전에 내가 balancing 을 한 것과 동일한 듯)
Evaluation metrics comparison
ROC AUC vs PR AUC
- roc auc 는 true positive rate(tp/(tp+fn)), false positive rate(1-tn/(fp+tn)를 보는 반면, pr auc 는 positive predictive value(tp/(tp+fp)), true positive rate(tp/(tp+fn))를 보게 됨
- positive class 가 더 중요하다면 이것에 대해 더 민감한 pr auc 가 더 나음(tn 을 전혀 보지 않음, positive 에 더 민감함)
- e.g.) fraud detection 등에서처럼 데이터가 imbalanced 되어있고, positive 가 더 중요한 경우
- 예시
- 총 데이터: 1,000,000개, Positive 데이터: 100개
- Model 1: 100개를 P로 predict했는데, 90개가 맞음. -> TP = 90, TN = 999890, FP = 10, FN = 10.
- Model 2: 2000개를 P로 predict했는데, 90개가 맞음. -> TP = 90, TN = 997990, FP = 1910, FN = 10.
- Model 1이 더 뛰어난 model임을 알 수 있다. 하지만 ROC curve의 TPR, FPR은 이에 대한 차등을 두지 않는다.
- ROC curve
- Model 1: 0.9 TPR, 0.00001 FPR
- TPR = TP/(TP + FN) = 90/(90 + 10) = 0.9
- FPR = FP/(FP + TN) = 10/(10 + 999890) = 0.00001
- Model 2: 0.9 TPR, 0.00191 FPR (difference of 0.0019)
- TPR = TP/(TP + FN) = 90/(90 + 10) = 0.9
- FPR = FP/(FP + TN) = 1910/(1910 + 997990) = 0.00191
- 이때 랜덤일 경우 roc auc 값은 0.5 (데이터 분포에 상관없이 항상 일정함)
- Model 1: 0.9 TPR, 0.00001 FPR
- PR curve
- Model 1: 0.9 precision, 0.9 recall
- Precision = TP/(TP + FP) = 90/(90 + 10) = 0.9
- Recall = TP/(TP + FN) = 90/(90 + 10) = 0.9
- Model 2: 0.045 precision (difference of 0.855), 0.9 recall
- Precision = TP/(TP + FP) = 90/(90 + 1910) = 0.045
- Recall = TP/(TP + FN) = 90/(90 + 10) = 0.9
- 랜덤일 경우 PR auc 값은 (100/1000000)*0.5
- Model 1: 0.9 precision, 0.9 recall
- ROC curve
- 위의 두 지표를 비교해봤을때 PR curve의 경우, 랜덤일경우에 대한 기준이 정해져있지 않기때문에(데이터 분포에 따라서 변하기때문에) 데이터 분포에 대한 파악없이, 숫자만으로 어떤 insight를 얻는 것이 쉽지 않다.
- 즉, 주기적으로 매일매일 성능을 확인해야하는 경우에는 pr auc 로는 daily의 추세등을 한눈에 파악하기 어려워서 적절하지 않은 것으로 보인다.