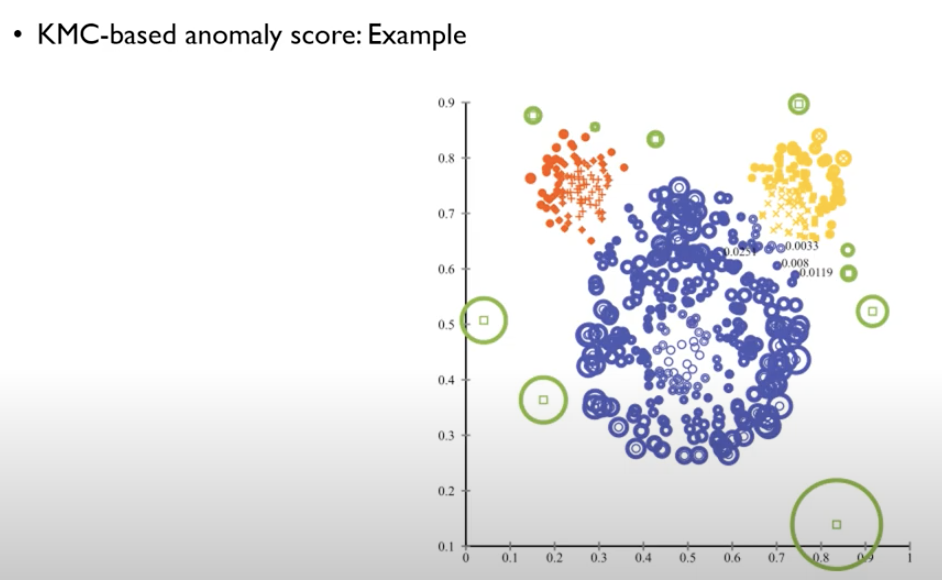
[Anomaly detection] Traditional way - Distance-based methods
K-nearest neighbor-based anomaly detection
- 이상치 데이터는 거리상으로 멀리 떨어져있을 것이라는 가정
- 이때엔 거리만으로 이상치 여부를 판단하고, normal class에 대해서 어떠한 사전분포도 가정하지 않는다.
k-nearest neighbor
- parzen window density estimation 에서
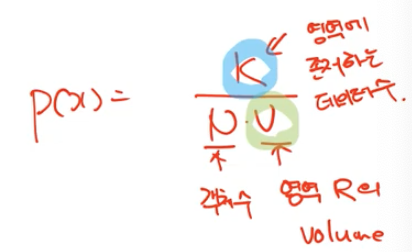
p(x)=k/(N*V) (k=영역에 존재하는 데이터의 수 , N=객체의 수, V=영역 R의 volumn) 에서 V를 고정시킨게 parzen window density estimation 이라면 k-nearest neighbor는 k를 고정시킨 것 (k를 커버하는 V를 추정하는 것) - k번째까지의 거리를 어떻게 측정할 것인가에 따라서 변종들이 있음
- max distance, average(개별적 거리를 먼저 계산 후 average), 평균까지의 거리(무게중심하나 놓고, 무게중심까지의 거리를 측정)
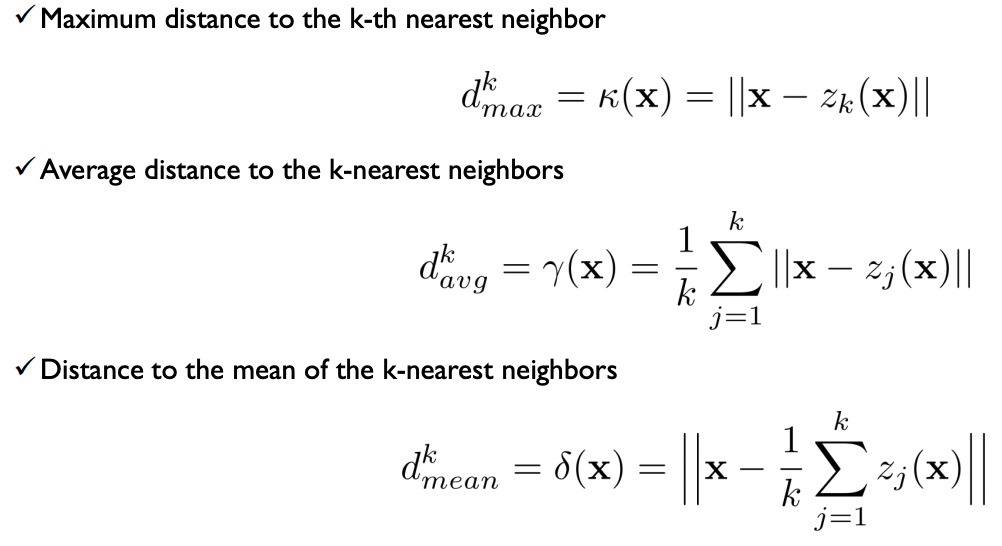
- 아래 그림에서처럼 측정 방법에 따라서 이상치 스코어가 달라진다.
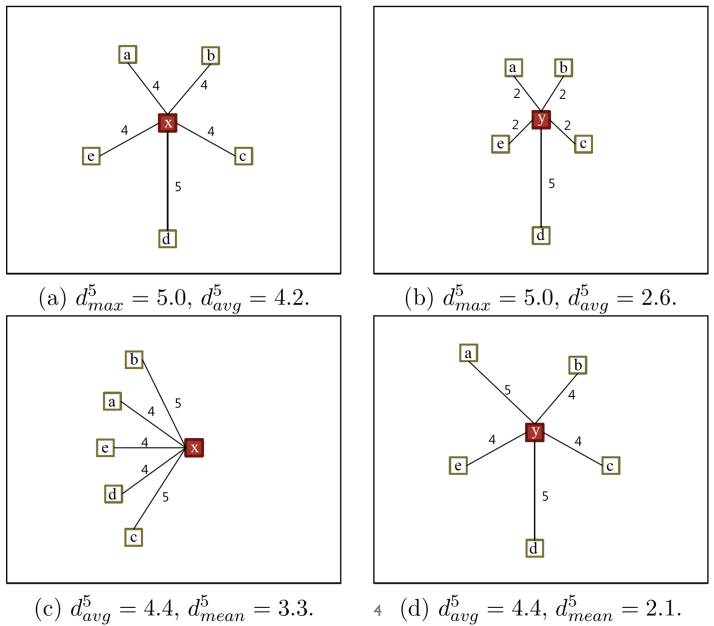
- max distance, average(개별적 거리를 먼저 계산 후 average), 평균까지의 거리(무게중심하나 놓고, 무게중심까지의 거리를 측정)
knn 기반 anonaly detection 에서의 반례
- knn 기반의 기법들이 찾아내지 못하는 반례들이 존재한다.
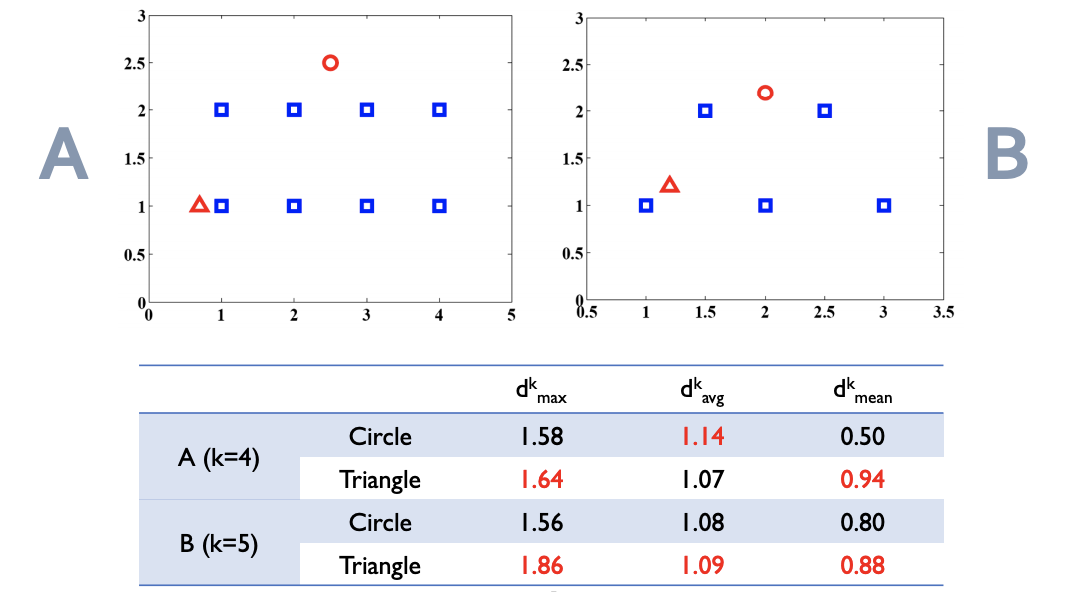
- 위 그림에서처럼 B에서의 세모는 polygon 내부에 있기때문에, 다른 어떤 점들 보다도 이상치 스코어가 더 낮아야한다. 또한 A, B에서 동그라미는 polygon 바깥에 있으므로 더 높은 이상치 스코어를 나타내야한다.
-> 그런데 그렇지 않음!
반례 보완
- A hybrid novelty score and its use in keystroke dynamics-based user authentication (PilsungKang, SungzoonCho, 2009)
- 보정 하는 factor 만듦
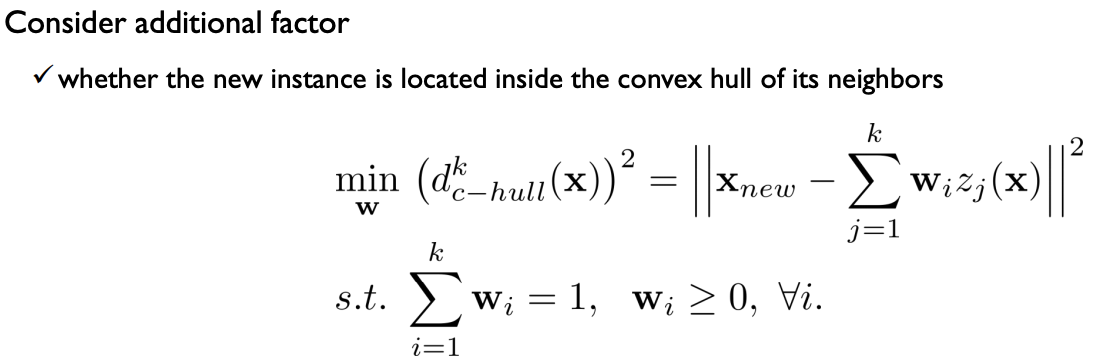
- 현재 알아보고자 하는 객체가 이웃들로 만들어지는 convex 안에 위치하는지 확인하는 것
- 객체(x)와 이웃(z(x))가 있을때, 이웃들을 x와 가장 유사하게 변형시키는 w를 찾아낸다.

- polygon 밖에 있다면(convex hull distance가 0이 아니라면) 분모가 커지면서 average distance 에 대한 penelty 부분이 증폭되게 된다.
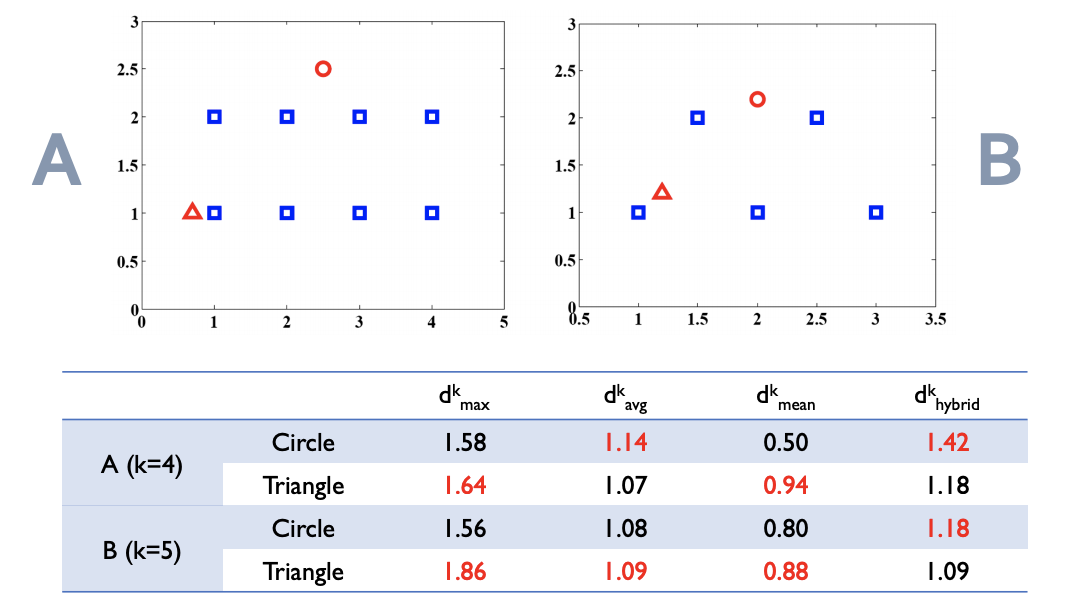
위의 그림상에서 보자면 원이 세모보다 더 큰 이상치 스코어를 갖게 되었다.
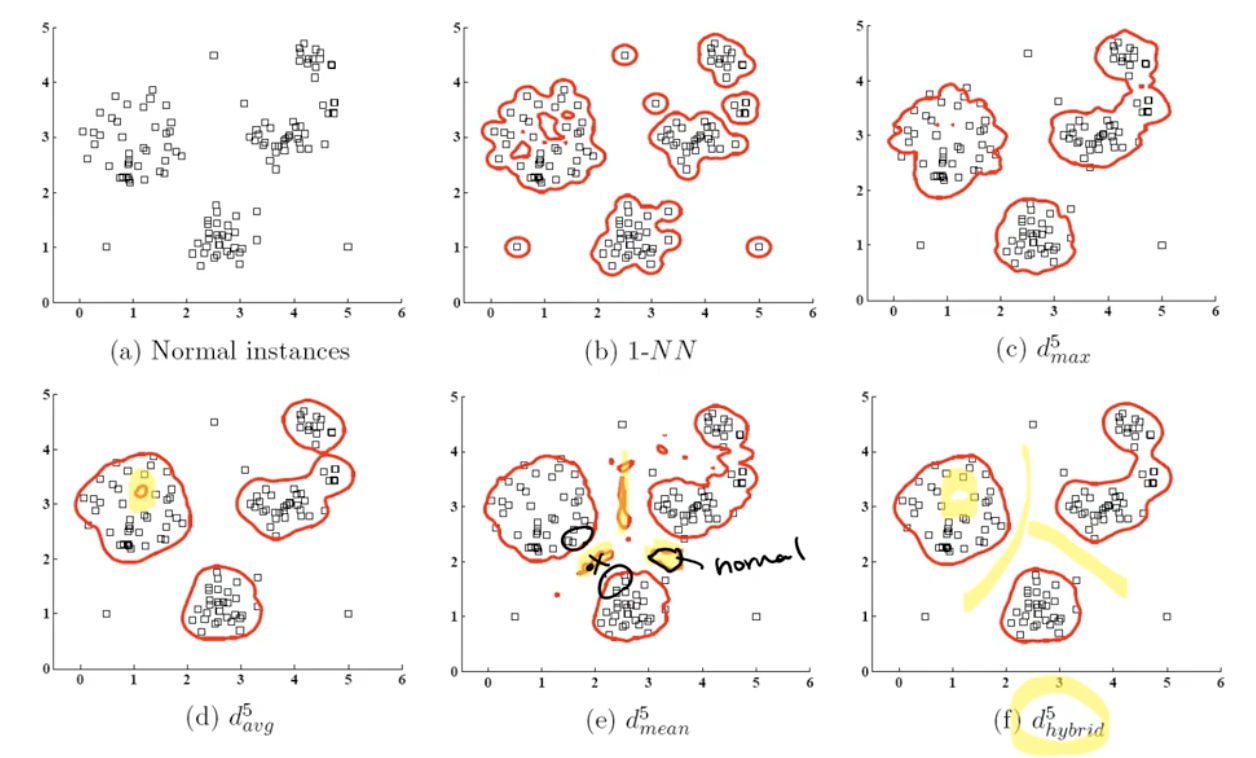
제안하는 score 를 이용했을때에(f) 밀도가 낮은 영역에 구멍이 뚫리는 현상도 사라지고, 밀도가 높은 영역 중간영역 또한 잘 구분해 내는걸 알 수 있었다.
총 21개의 데이터에 대해서 14개 알고리즘을 30회 반복 실험을 했을때(21*14*30)에 더 좋은 결과를 보여주었다.
Clustering-based approach
- DBSCAN 같은 알고리즘은 군집에 속하지 않은 객체들은 전부 이상치로 취급한다
- 이 외에 일반적인 clustering algorithm을 이용해서도 이상치 판단이 가능함.
-가장 가까운 군집과의 거리가 멀 경우 이상치로 판단하는 것이 그 방법이다.

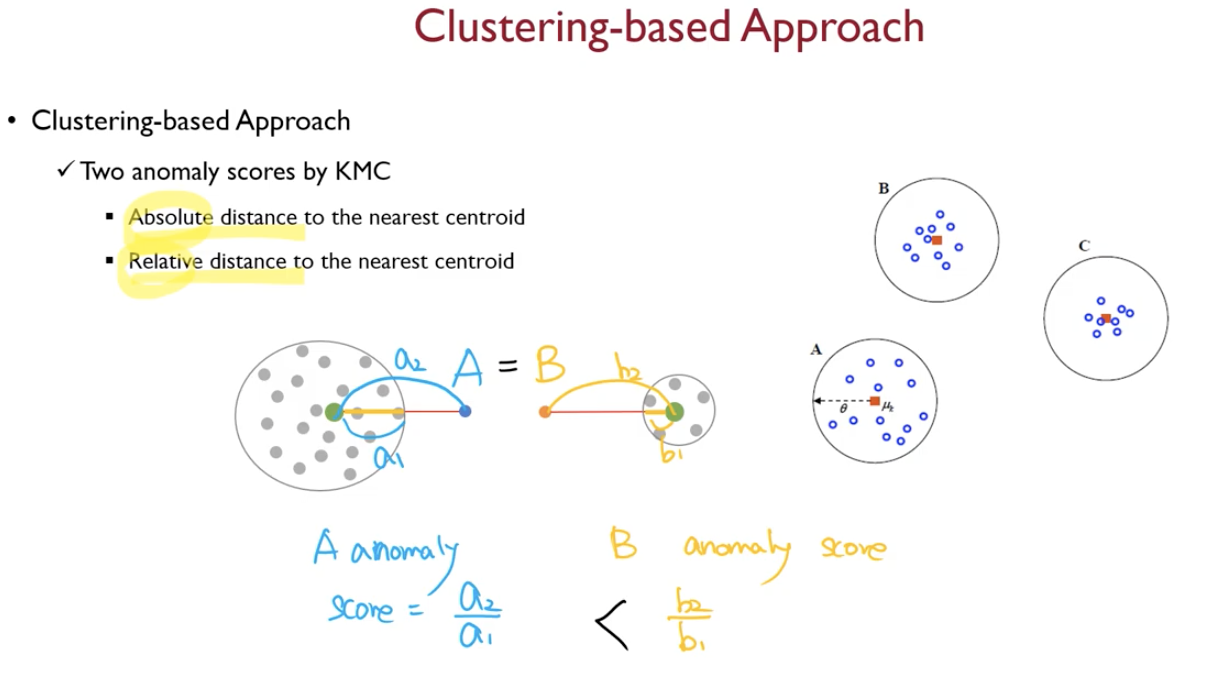
- k means clustering을 진행한 후, 이상치를 판단하는데, 그 판단에는 아래의 두 방식이 존재한다.
- absolute distance to the nearest centroid
- 가장 가까운 centroid 까지의 거리를 구한다
- relative distance to the neariest centeroid
- 군집의 지름을 계산해서, 군집 지름대비 얼마나 더 멀리떨어져있는지로 계산
- kmeans based anomaly score 를 sklearn 에서 제공하고 있는데 그걸 이용하면 아래와 같이 나타난다.