
Multiple Linear Regression
- Linear Regression with several variables.
- 입력이 하나가 아니고 x1, x2, ... xn 여러 개인 경우
Multiple인 경우 Gradient Descent를 어떻게 적용하는가?
- Easier, performed separately for each parameters.
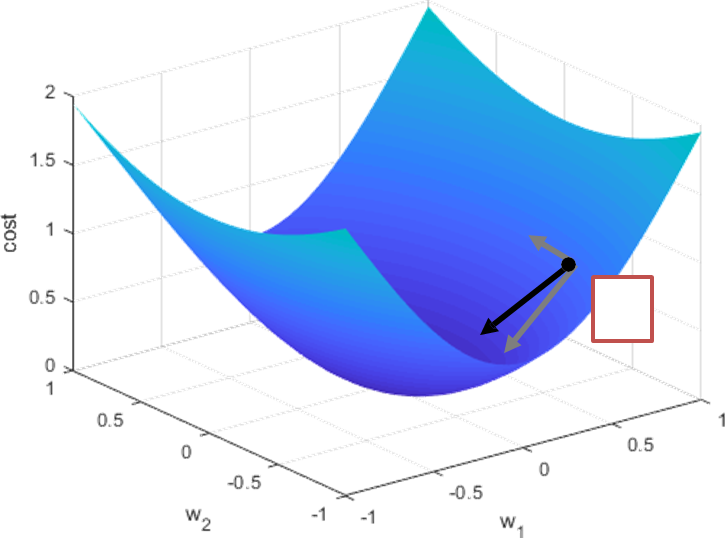
- W가 두 개인 경우, 3차원으로 표현된다.
- 각 축에 대하여 따로 미분한 후 합친다. 까만 벡터로 점프.
Example
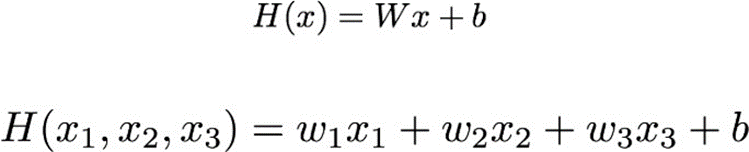
- Multiple인 경우, 여러 개의 w 존재.
- 라지 W로 표현한다.
[5, 3] x [3, 1] = [5, 1]
- b가 없다고 가정하면,
X는5 by 3이고 H(X)는5 by 1이므로
W는3 by 1이다.
Logistic Regression
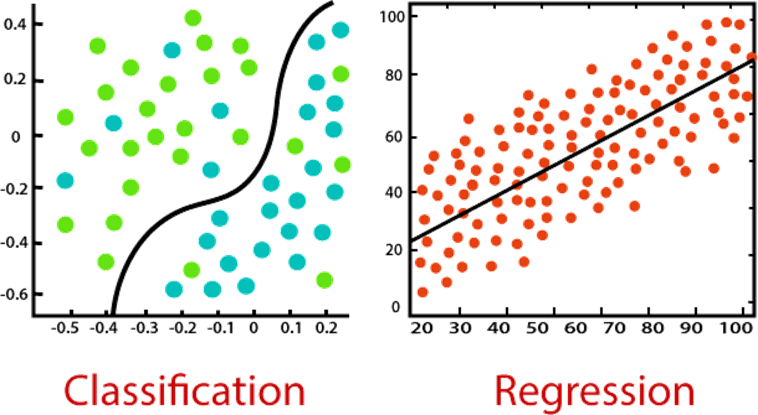
Regression 주어진 데이터들을 바탕으로 예측
Classification 확률 값을 출력하는 Logistic을 통해서 분류
Standard Logistic Function
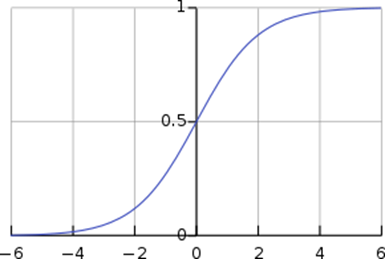
Logistic이란?
- 그래프를 그렸을 때, logistic function인 것
- True or False로 말할 수 있는 것
함수 별 shape과 식을 알아야 한다.
// Logistic function == Sigmoid function
Convex vs 미분가능
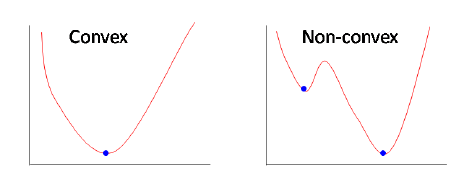
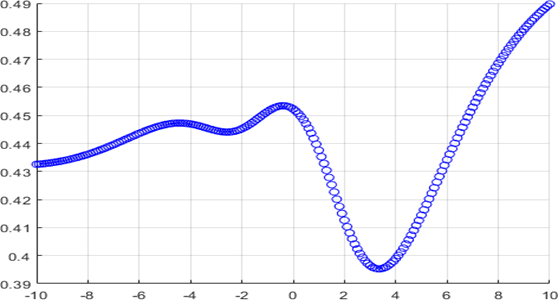
- Convex != 미분가능
- 위 그래프는 local minimum이 존재한다. (convex가 아니다)
- 그러므로 Gradient Descent 방식을 적용할 수 없다.
Logistic의 Cost Function
- 해결책은 new cost function 사용
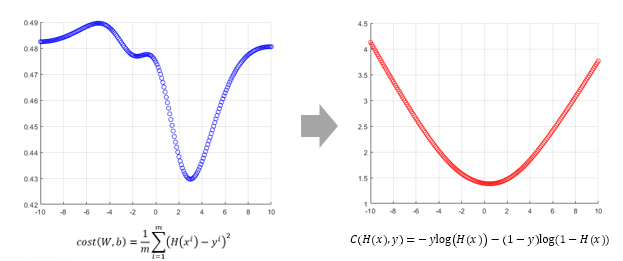
- 아래의 두 식을 합쳐서 하나의 식으로 표현
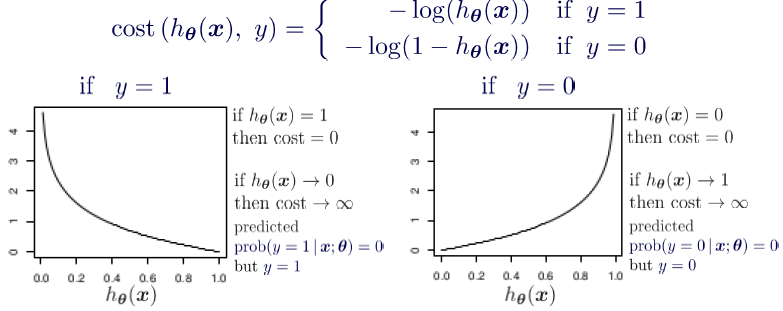
- 이제 convex하므로 Gradient Descent를 적용할 수 있다.
- 즉, Linear Regression으로 해결할 수 있다.
📌 Note
- Gradient Descent를 적용할 수 없는 이유 -> Local minima 존재
- Cost function 그래프 그릴 수 있어야 함

