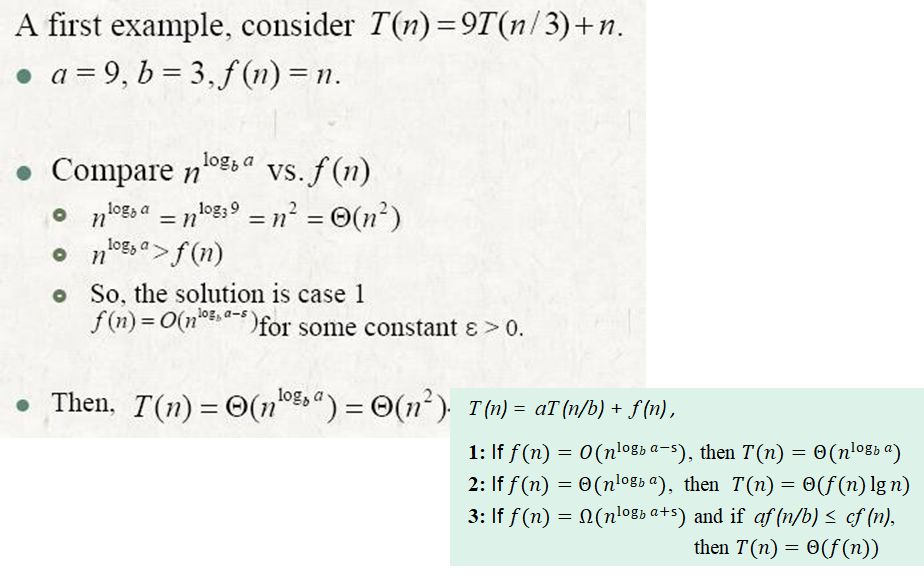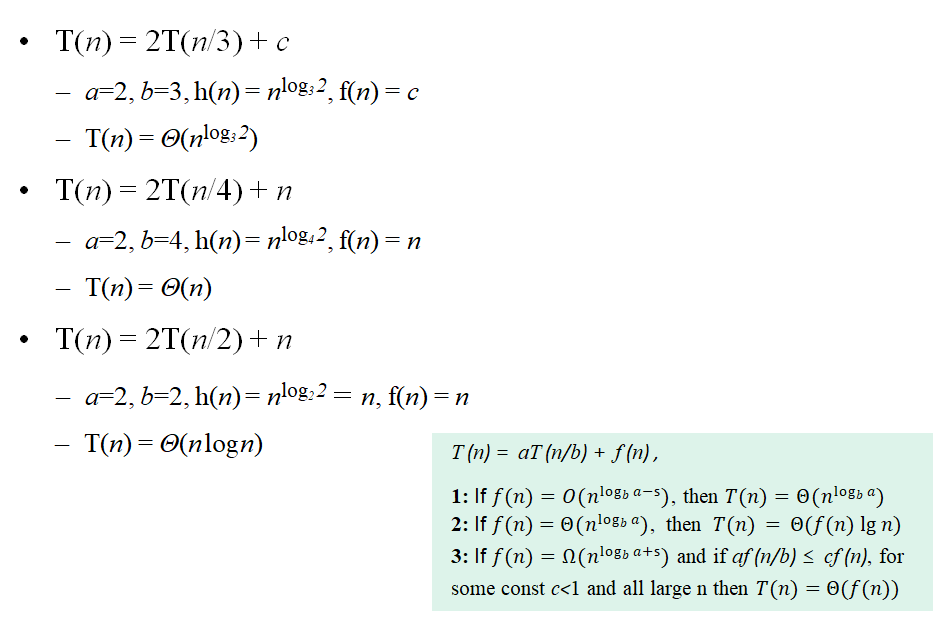점화식
- 알고리즘이 자신에 대한 재귀 호출을 포함하는 경우 실행 시간은 종종 재귀로 설명될 스 있음
- 반복은 더 작은 입력의 값으로 함수를 설명하는 방정식 또는 부득식
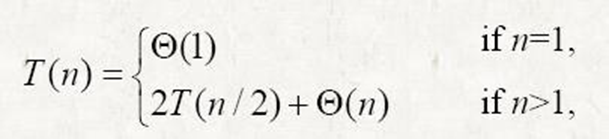
Merge Sort: conquer & merge
Quick Sort: conquer & divide
- 점화식 풀이
- 솔루션에서 점근적 “Θ”, “O” 범위를 얻음
- 점화식을 푸는 3가지 방법
- Substitution(치환) 방식
- Recursion-tree(재귀 트리) 방식
- Master 방식
- 점화식은 다음과 같이 정의된 함수
- 하나 이상의 base case 및 더 작은 인수가 있는 자체

Technicality 전문적 사항
- 기술적 세부 사항의 무시
- The assumption of integer arguments: 정수 인수의 가정
- Boundary condition: 경계 조건
- Floors and ceilings: 바닥과 천장
정수 인수의 가정 생략
- 실행시간 T(n)은 n이 정수일 때만 정의됨
- 예를 들어 Merge sort의 최악 시간에 대한 점화식
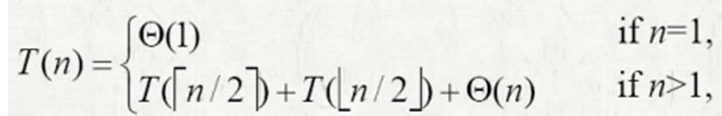
- 그러나 일반적으로는 다음가 같이 표현됨
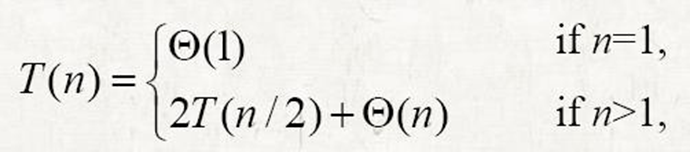
경계 조건 생략
- 경계 조건은 T(n)이 일반적으로 작은 n에 대해 상수임
- 예를 들어

바닥과 천장 생략
- 바닥과 천장은 중요하지 않지만 때때로 중요함
점화식 풀이 방식
반복 대체 방법
- 치환 방식: 한도를 추측한 다음 수학적 귀납법을 통해 추측이 정확함을 증명함
- 마스터 방식
- 양식의 반복에 대한 범위를 제공
- T(n) = aT(n/b) + f(n), 여기서 a>=1, b>1, f(n)은 주어진 함수
- 재귀트리 방시
- 점화식을 노드가 나타내는 트리로 변환함
- 재귀의 다양한 수준에서 발생하는 비용


The substitution method 치환 방식
- 솔루션을 추측함
- 추측이 옳다는 것을 증명하기 위해 수학적 귀납법 사용
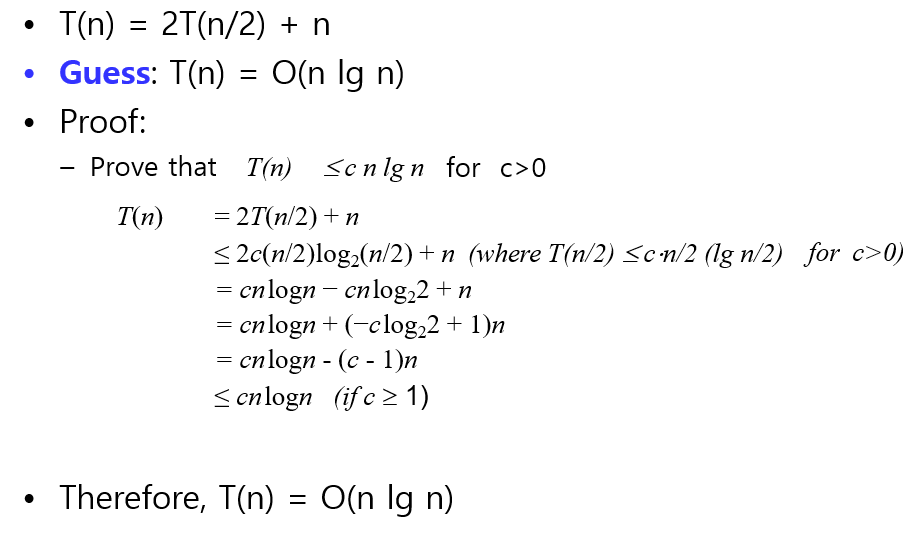
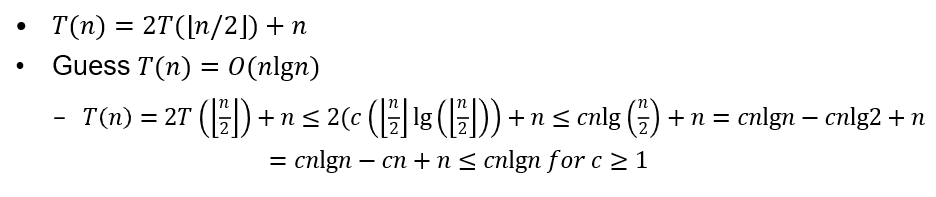
- 모든 n에 대해 T(n) = cnlgn를 증명할 필요는 없음
- T(n) = n >= n0에 대한 cnlgn만 증명하면 됨
- n > 3의 경우 점화식이 T(1)에 직접적으로 의존하지 않다는 것을 관찰해라
- 따라서 n0 = 2로 해서 base case로 T(1)을 T(2) 및 T(3)으로 대체할 수 있음
- T(1) = c1lg1 = 0
- T(2) = 4 and T(3) = 5
- T(2) = 4 <= c2log2 and T(3) = 5 <= c3lg3
- c >= 2를 선택하면 위의 부등식을 충족함
base case가 무조건 T(1)이 되진 않아도 됨

- 값 변경
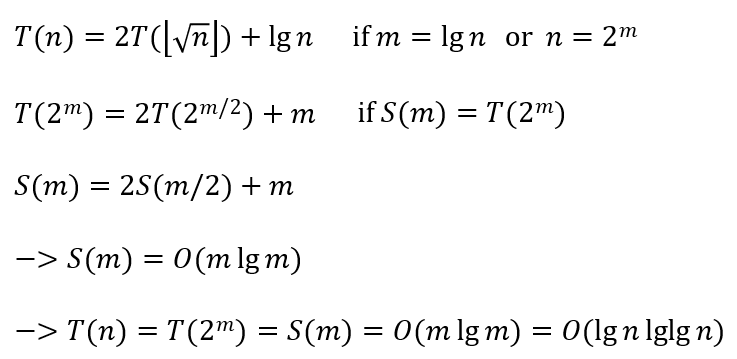
The recursion-tree method 재귀 트리 방식
- 각 코드는 재귀 함수 호출 집합의 어딘가에 있는 단일 하위 문제의 비용을 나타냄
- 트리의 각 수준 내에서 비용을 합산해 수준별 비용 집합을 얻음
- 그런 다음 모든 수준별 비용을 합산해 모든 재귀 수눙의 총 비용을 결정함
- 분할 정복 알고리즘의 실행 시간을 설명하는 반복을 해결하는 데 유용함
- 대체 방법으로 확인되는 좋은 추측을 생성하는 데 사용됨
- 재귀 트리를 주의 깊게 그리고 비용을 합산하면 재귀에 대한 솔루션의 직접적인 증거로 사용할 수 있음
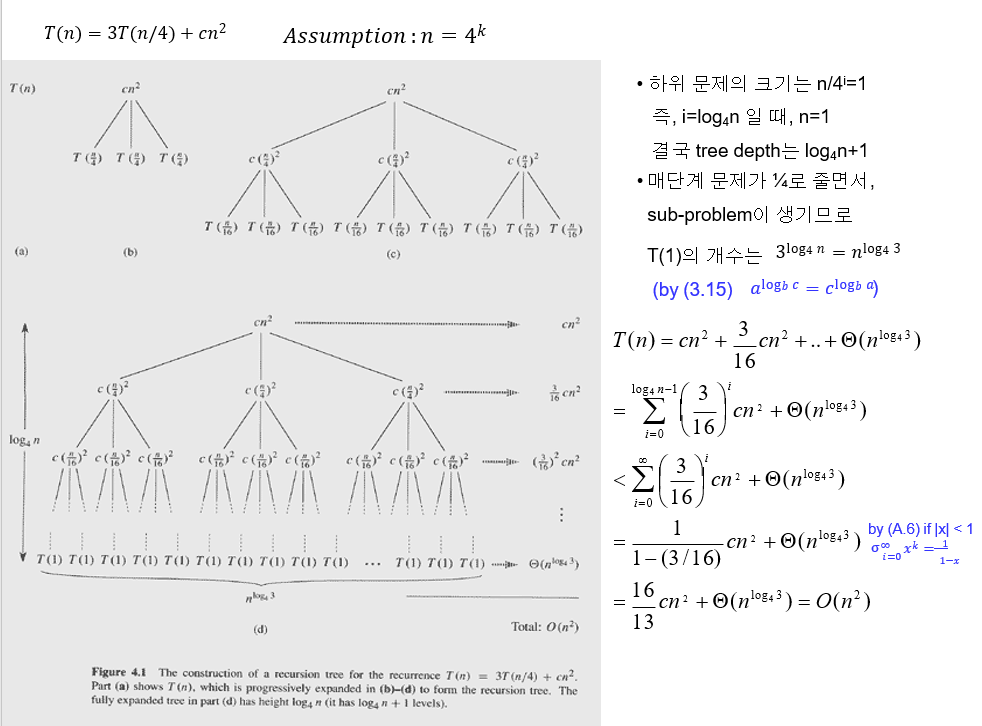
- T(n) <= dn^2(d>0, c>0)
- T(n) ≤ 3T(⌊n/4⌋) + cn2
≤ 3d⌊n/4⌋ 2 + cn2
≤ 3d(n/4)2 + cn2
= 3/16 dn2 + cn2
≤ dn2
-> d >= (13/16)cT(n) = Ω (n2) and T(n) = O(n2), T(n) = Θ(n2)
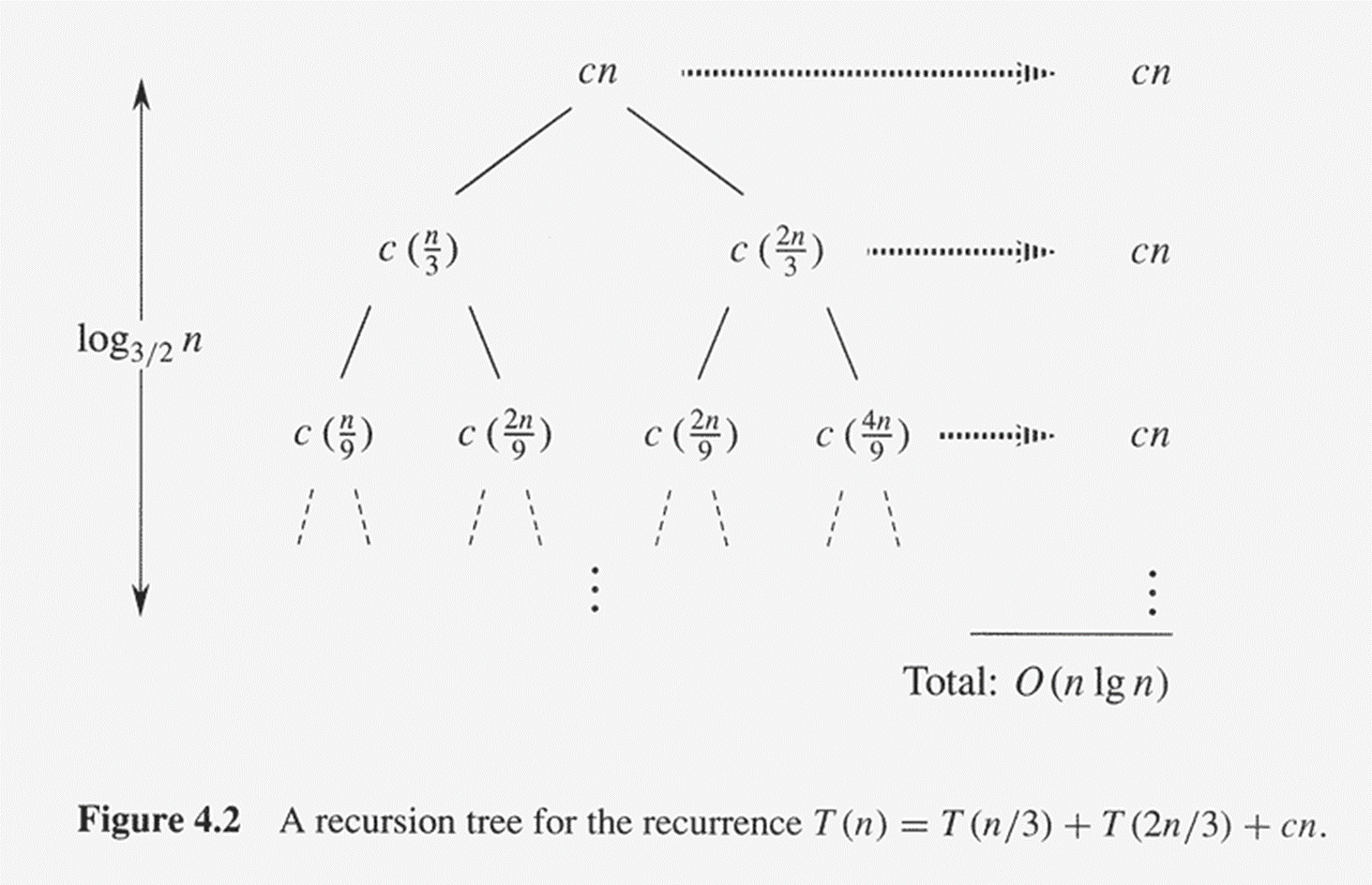
- 상한 O(nlgn) 증명
- 일부 상수 d에 대해 T(n) ≤ dnlgn임을 보여줌
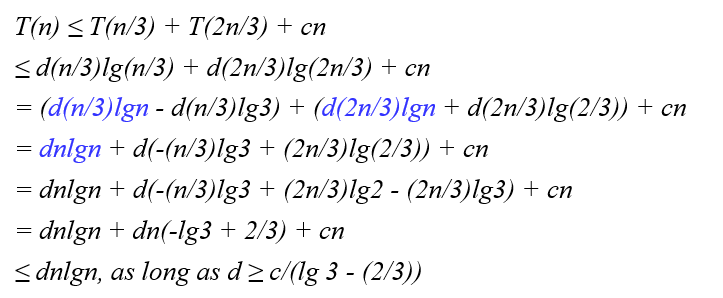
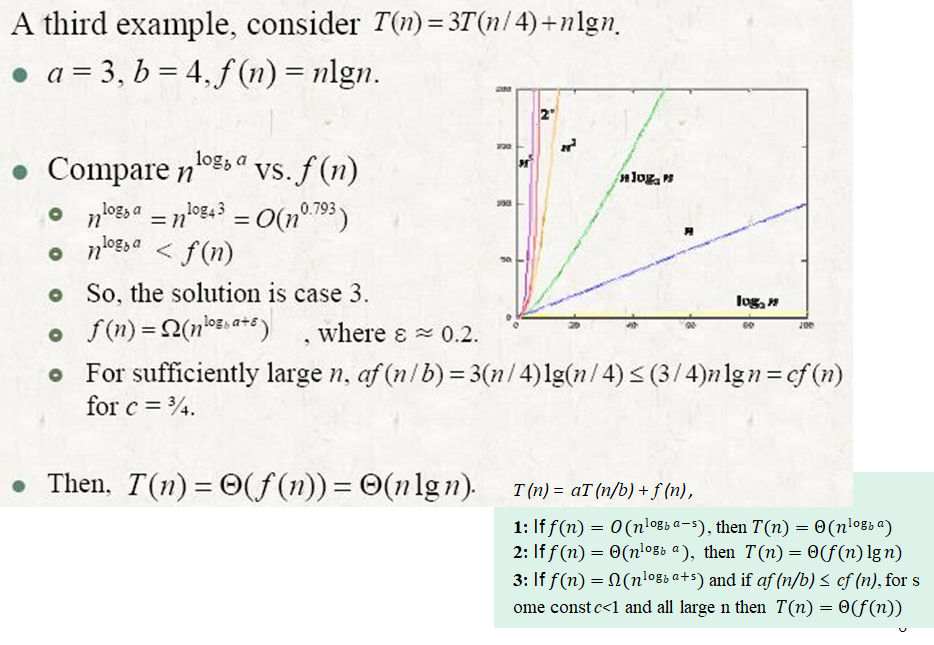
The Master Method
- 마스터 방법은 양식의 반복을 해결하기 위한 "요리책" 방법을 제공
- T(n) = aT(n/b) + f(n)
여기서 a ≥ 1 및 b > 1은 상수이고 f(n)은 점근적으로 양의 함수임
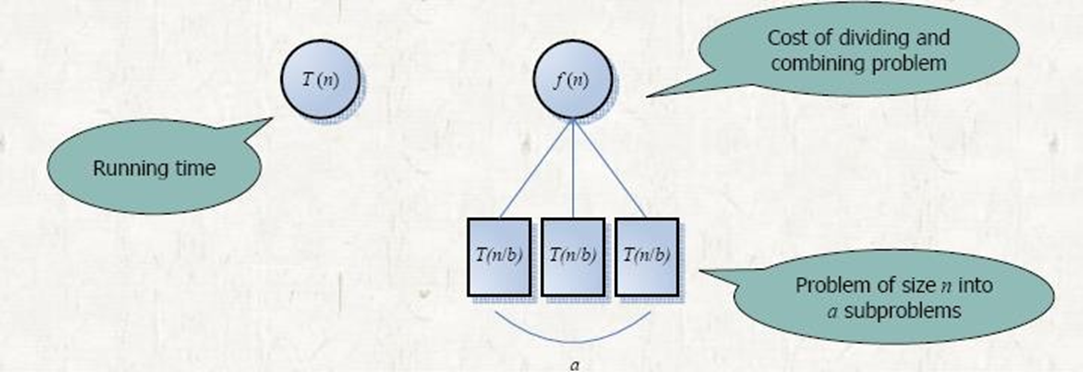
- a ≥ 1, b > 1은 상수, f(n)은 함수, T(n)은 재귀에 의해 음이 아닌 정수에 대해 정의됨
T(n) = aT(n/b) + f(n)
n/b는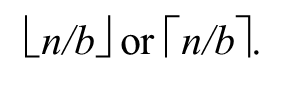
를 의미하는 것으로 해석함
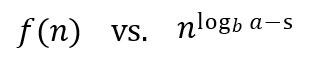
- 두 가지를 비교함