모듈러 연산의 성질
Zn에서의 연산
- 최소 잉여 집합 Zn에 대해 덧셈, 뺄셈 곱셈 연산 수행 가능
- 임의의 두 정수 a, b ∈ Z ∈ Zn에 대한 덧셈, 뺄셈, 곱셈 연산
- 입력 값: a, b ∈ Z or Zn
- 출력 값: c ∈ Zn
(a+b) mod n = c
(a-b) mod n = c
(axb) mod n = c
- 예) 입력값을 Zn에서 선택해 아래 문제를 계산하시오
- Z15의 7과 14를 더하시오.
(7+14) mod 15 = 6 - Z13의 7에서 11을 빼시오.
(7-11) mod 13 = 9 - Z20의 7과 11을 곱하시오.
(7x11) mod 20 = 17
모듈러 연산의 성질
Property 1. (a + b) mod n =[(a mod n) + (b mod n)] mod n
Property 2. (a - b) mod n =[(a mod n) - (b mod n)] mod n
Property 3. (a x b) mod n =[(a mod n) x (b mod n)] mod n
Property 4. 10^n mod x = (10 mod x)^n mod x (Property 3을 n번 적용한 결과)
상기 모듈러 연산의 성질을 왜 이해해야 하는가?
- 암호 알고리즘에 모듈러 연산 적용 시 a와 b의 값은 일반적으로 매우 큰 수
- 따라서 계산 시 발생하는 오버헤드 완화할 수 있음
모듈러 역원
덧셈에 대한 역원
-
모듈러 연산에서 각각의 정수는 덧셈에 대한 역원을 가짐
-
어떤 정수 a와 그 정수의 덧셈에 대한 역원 b의 합은 모듈러 n에 대해 0과 합동
-
Zn에서 두 수 a와 b는 다음과 같이 서로 덧셈에 대한 역원이 됨
a+b ≡ 0 (mod n)
-
Zn에서 a의 덧셈에 대한 역원은 b = n - a
a+b는 n으로 나눠떨어지면서 최대 크기가 n임(모듈러 연산 결과가 0이기 때문)
-
예) Z10에서 모든 덧셈에 대한 역원의 쌍들을 구해라
(0, 0), (1,9), (2,8), (3,7), (4,6), (5,5)- 0은 0 자신이 덧셈에 대한 역원
a+b가 0이 될 수도 있기 때문에
- 0은 0 자신이 덧셈에 대한 역원
-
덧셈에 대한 역원은 역관계임
곱셈에 대한 역원
- Zn에서 두 정수 a, b가 아래의 성질을 만족하면 이들은 서로 곱셈에 대한 역원이 됨
a x b ≡ 1 (mod n)
- 모듈러 연산에서 정수는 곱셈에 대한 역원이 있을 수도 있고, 없을 수도 있음
- 만약 곱셈에 대한 역원이 있다면, 그 정수와 해당하는 곱셈에 대한 역원의 곱은 모듈러 n에서 1과 합동임
- a가 Zn에서 곱셈에 대한 역원을 갖기 위한 필요충분조건
- gcd(n, a) = 1
- n과 a는 서로소임
역원: 역수가 나오는 것
만약 역원이 존재한다 -> 복호화가 가능하다
-
예) Z10에서 8의 곱셈에 대한 역원을 계산하시오
gcd(10, 8) = 2 != 1이므로 곱셈에 대한 역원이 존재하지 않음- Z10에서 8을 곱해 그 결과가 1과 합동이 되는 수를 0부터 9사이에서 찾을 수 없음
-
예) Z10에서 곱셈에 대한 모든 역원을 계산하시오
- Z10에서 세 쌍의 역원 (1, 1), (3,7), (9,9)가 존재함
- (1 x 1) mod 10 = 1
- (3 x 7) mod 10 = 1
- (9 x 9) mod 10 = 1
곱셈에 대한 역원과 확장 유클리드 알고리즘
- 확장 유클리드 알고리즘에서 n과 b가 주어지고 역원이 존재할 때, Zn에서 b의 곱셈에 대한 역원을 구할 수 있음
- 첫 번째 정수 b를 모듈러 n으로 대체함
- 확장 유클리드 알고리즘을 이용하여 sn+bt=gcd(n,b)를 만족하는 s와 t를 구함
- b의 곱셈에 대한 역원이 존재한다면 gcd(n,b)=1이어야 함.
따라서 (sn + bt) = 1을 만족해야 함 - 양변에 대한 모듈러 연산을 적용함
좌변과 우변을 Zn에 대응시키면 (b x t) mod n = 1
Zn에서 t가 b의 곱셈에 대한 역원임을 의미함
-> b의 곱셈에 대한 역원은 t를 Zn에 대응시킨 값임
- 예) Z26에서 11의 곱셈에 대한 역원을 구하시오
r1 = 26, r2 = 11
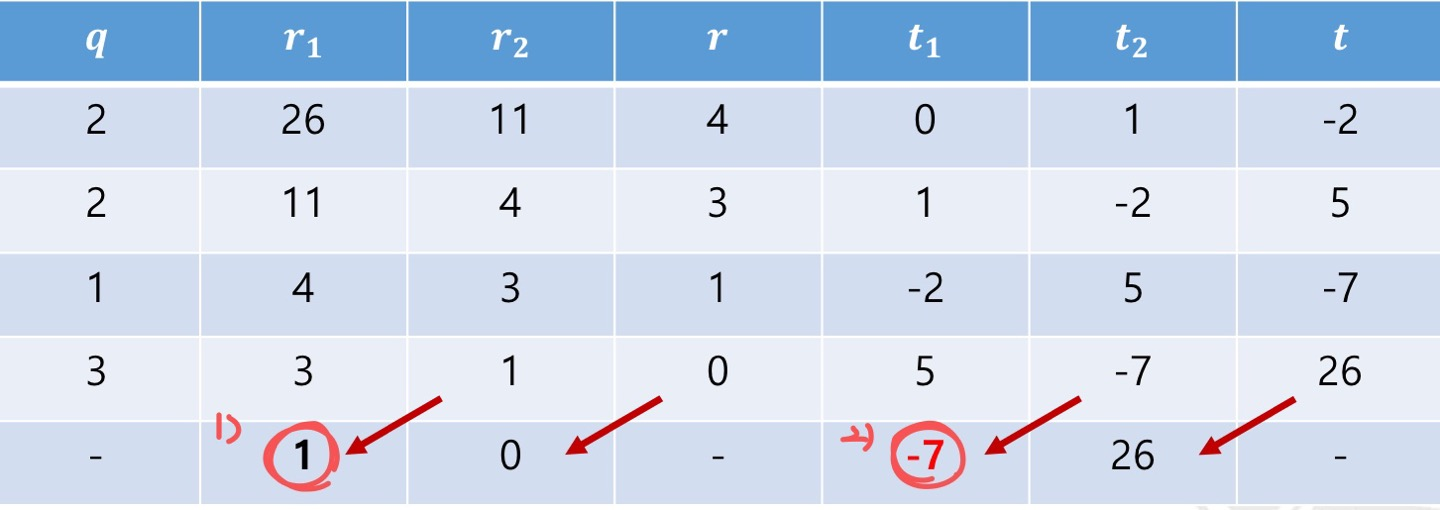
1) r = 1 -> 최소공배수 1이므로 11의 곱셈에 대한 역원이 존재함
2) 확장 유클리드 알고리즘을 이용해 t = -7을 얻음
3) 곱셈에 대한 역원은 (-7) mod 26 = 19 -> 11과 19는 Z26에서 곱셈에 대한 역원임
4) (11 x 19) mod 26 = 209 mod 26 = 1
예) Z26에서 12의 곱셈에 대한 역원을 계산하시오
gcd(26, 12) = 2 != 1 -> 곱셈에 대한 역원이 존재하지 않음
예) Z100에서 23의 곱셈에 대한 역원을 계산하시오
r1 = 100, r2 = 23
1) r = 1 -> 최소공배수 1이므로 11의 곱셈에 대한 역원이 존재함
2) 확장 유클리드 알고리즘 -> t = -13
3) 곱셈에 대한 역원은 (-13) mod 100 = 87 -> 23과 87은 Z100에서 곱셈에 대한 역원
4) (23 x 87) mod 100 = 20001 mod 100 = 1 성립함
덧셈표와 곱셈표
덧셈표
덧셈에 대한 역원은 항상 존재함
- 덧셈의 역원 = 덧셈의 결과가 0인 경우
곱셈표
곱셈에 대한 역원은 존재할 수도 있고 존재 안 할 수도 있음
- 곱셈의 역원 = 곱셈의 결과가 1인 경우
덧셈과 곱셈에 대한 다른 집합
-
암호에서 역원이 어떻게 사용되는가?
- 송신자가 암호화 키로써 정수를 사용
- 수신자는 복호화 키로써 해당 정수의 역원을 사용
- 만약 암/복호화 알고리즘의 연산이 덧셈 -> Zn에 속한 모든 정수가 덧셈에 대한 역원을 가짐 -> Zn이 가능한 키의 집합으로 사용
- 만약 /암복호화 알고리즘의 연산이 곱셈 -> Zn에 속한 일부 정수만이 곱셈에 대한 역원을 가짐 -> Zn은 가능한 키의 집합이 안 됨
- 이 경우, 곱셈에 대한 역원을 갖는 원소 집합을 사용해야 함
- Zn*: Zn의 부분 집합으로 Zn에 속한 정수 중 곱셈에 대한 역원을 가진 원소들을 모아놓은 것
- Zn*는 곱셈표로부터 직접 생성 가능
덧셈에 대한 역원이 필요할 때: Zn
곱셈에 대한 역원이 필요할 때: Zn*

