추가 예제(2) - 피보나치수
-
피보나치 수열의 정의

-
n번째 피보나치수 구하기

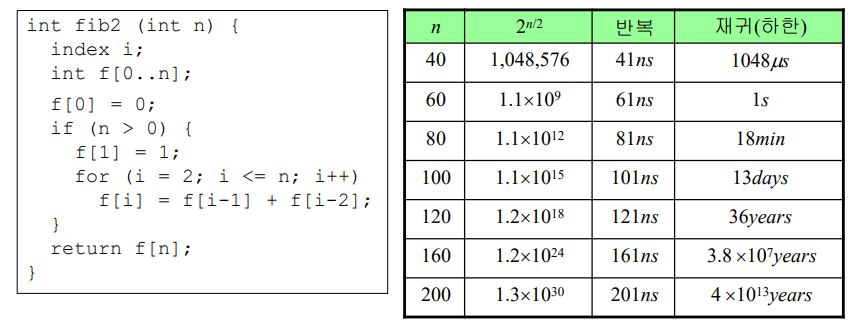
피보나치수열 재귀알고리즘 분석
- 피보나치수 구하기 재귀 알고리즘은 수행속도가 매우 느림
- 이유: 같은 피보나치 수를 중복 계산
- 예) fib(5)계산에 fib(2) 3번 중복 계산
- T(n) = fib(n)을 계산하기 위하여 fib 함수를 호출하는 횟수
- 즉, 재귀 트리 상의 마디의 개수

- 즉, 재귀 트리 상의 마디의 개수
정리: 재귀적 알고리즘으로 구성한 재귀 트리의 마디의 수를 T(n)이라
하면, n >= 2인 모든 n에 대하여 T(n) > 2n/2 이다.
피보나치수열 반복 알고리즘 분석
- T(n) = n
- 훨씬 바른 결과 획득 가능
- 하지만 SP(n) = n
- SP(n) = 4로 개선 가능
Class Outline
- Problem
- Why the problem?
- Problem definition.
- Algorithm
- Description: 묘사
- Correctness: 정확성
- Correct output for every legitimate input in finite time: 유한 시간 내의 모든 합법적인 입력에 대한 올바른 출력
- Based on correct math formula: 올바른 수학 공식을 기반으로 함
- By induction 귀납으로
- Performance 성능
기본 데이터 구조
Linear data structures: 선형 데이터 구조
- Array, Linked list, Stack, Queue 배열, 연결된 목록, 스택, 대기열
- Operations: search, delete, insert 작업: 검색, 삭제, 삽입
- Implementation: static, dynamic 구현: 정적, 동적
Non-linear data structures: 비선형 데이터 구조
- Graphs
- Trees : connected graph without cycles 사이클 없이 연결된 그래프
- Rooted trees
- Ordered trees
- Binary trees 이진트리
- 𝑙𝑜𝑔2𝑛 ≤ ℎ ≤ 𝑛 − 1 n개의 노드가 있는 이진 트리의 높이 h에 대해
- Graph representation: adjacency lists, adjacency matrix Tree representation: as graphs; binary nodes
• 그래프 표현: 인접 목록, 인접 행렬 트리 표현: 그래프로, 이진 노드
- Rooted trees
Sets, Bags, Dictionaries
- Sets: 구별되는 요소의 순서없는 집합
- Operations: 멤버십, 유니온, 교차로
- Representation: 비트 벡터(선형 구조)
- Bags: 순서가 없는 컬렉션, 요소가 반복될 수 있음
- Dictionary: 작업 검색, 추가, 삭제가 포함된 Bag
알고리즘 분류
- 문제 유형별
- 설계 기법별: 문제를 해결하기 위한 일반적인 접근법
- Brute Force
- Divide-and-Conquer
- Decrease-and-Conquer
- Transform-and-Conquer
- Space and Time Tradeoffs
- Dynamic Programming
- Greedy Techniques
정렬

Insertoin sort
- Description: 묘사
- Correctness: 정확성
- Performance: 성능
Description
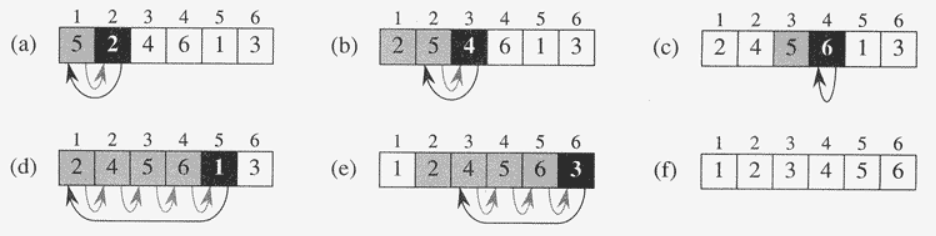
- Insertion sort: 삽입을 이용한 정렬 알고리즘
- Insertion이란?
- 키와 정렬된 키의 목록이 제공되면 정렬된 순서를 유지하는 정렬된 키 목록에 키를 삽입함

Correctness
- 루프 불변 사용 (Use a loop invariant)
- loop invaiant: 루프에 대한 "외부"의 각 반복이 시작될 때
- 루프 불변량을 사용하여 정확성을 증명하려면 다음 세
가지를 보여줌
- 초기화: 루프의 첫번째 반복 전에 true
- 유지관리: 루프가 반복되기 전에 참이면 다음 반복 전에 참으로 유지
- 종료: 루프가 종료될 때, 불변량의 일반적으로 루프가 종료된 이유와 함께 알고리즘이 정확하는 것을 보여주는 유용한 속성을 제공함
알고리즘 분석
- RAM 모델
- 명령은 순차적으로 실행됨
- 알고리즘의 실행 시간을 어떻게 분석하는가?
- 알고리즘에 걸리는 시간은 입력에 따라 다름
- 알고리즘에 의해 사용되는 명령어의 수를 계산함
- 실행 시간: 특정 입력에서 실행된 원시 연산(단계)의 수임
- 알고리즘 실행 시간은 입력 크기 n의 함수 (T(n))로 설명됨

tj = j의 해당 값에 대해 루프 테스트가 실행되는 동안의 횟수

- Best case: 배열이 이미 정렬됨 (모든 tj = 1)
- Worst case: 배열이 역순 (tj = j)
최악의 경우 실행 시간은 모든 입력에 대해 실행 시간에 대한 보장된 상한을 제공함 - Average case:평균적으로, A[j]의 key는 A[1...j-1]의 절반 미만이고 나머지 절반보다 큽니다. (tj = j/2).
Order of Growth
- 분석을 용이하게 하고 중요한 기능에 초점을 맞추기 위한 추상화
- 실행시간에 대한 공식의 선행 항만 봄
- 하휘학을 삭제하고 선행 항에서 상수 계수는 무시함
Example: an² + bn + c = Θ(n²)
- 하위 항 삭제 -> an²
- 상수 계수 무시 -> n²
- 최악의 경우 실행 시간 T(n)은 n²처럼 증가하며 n²와 다름
- 실행 시간은 성장 순서가 n²라는 개념을 포착하기 위해 π(n²)
- 최악의 경우 실행 시간이 증가 순서(T(n0, 흔히 시간 복잡도라 함)가 작을 경우 하나의 알고리즘이 다른 알고리즘보다 더 효율적이라고 생각함
Insertion sort의 공간 복잡도
- Θ(n)
- 입력 숫자가 제자리(in place, 원본 공간)에서 정렬됨
Divide and Conquer
- 문제를 여러 하위 문제로 나눔
- 하위 문제를 반복적으로 해결하여 해결함
- 기본 케이스: 하위 문제가 충분히 작으면 문제를 해결함
- 하위 문제 솔루션을 결합하여 원래 문제에 대한 해결책을 제공함
cf) 증분법: 삽입 정렬
Merge Sort
- Merge sort란 병합을 사용하는 정렬 알고리즘

- Merge의 실행 시간
- n1과 n2는 정렬된 두 목록의 길이를 나타냄
- Θ(n1 + n2) 시간
- 주요 작업: 비교 및 이동
- comparision <= movement
- movement = n1 + n2
- comparision <= n1 + n2
- comparision + movement <= 2(n1 + n2)
-> Θ(n1 + n2)를 의미함
-
분할 및 정복에 기반한 정렬 알고리즘
-
최악의 경우 실행 시간: merge sort < insertion sort를 증가순으로 정렬함
-
A[p . . r]를 정렬하려면
- 두 개의 서브 배열 A[p .. q]와 A[q+1 .. r]로 나누어라. 여기서 q는 A[p .. r] 의 중간점
- 두 개의 하위 배열 A[p...q]와 A[q+1]을 재귀적으로 정렬하여 정복함
- 단일 정렬 하위 배열 A[p...r]를 생성하기 위해 정렬된 두 하위 배열 A[p...q]와 [q+1]을 병합하여 결합함
- 이 단계를 수행하기 위해 MERGE(A, p, q, r) 절차를 정의함
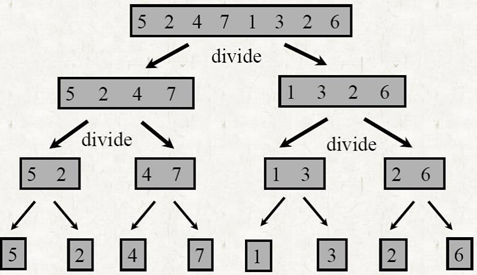
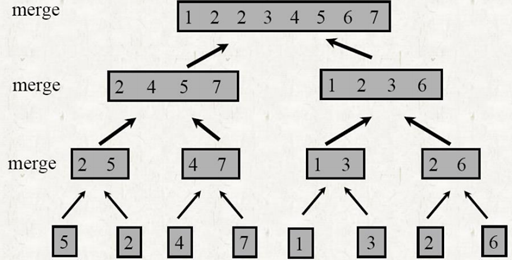


- 하위 배열 A[p...q]가 정렬되고 하위 배열 A[q+1]가 정렬됩니다.. r] 정렬됨
- p, q, r에 대한 제한으로 인해 두 하위 배열 모두 비어 있지 않음
- T(n) = σ(n), 여기서 n=r-p+1 = 병합되는 요소의 개수
- n = 주어진 (하위) 문제의 크기
- 분할 및 정복 알고리즘의 실행 시간을 설명하려면 반복(방정식)을 사용
- 크기 n의 문제에 대해 T(n) = 실행 시간이라고 하자.
- 문제의 크기가 충분히 작으면(상수 c의 경우 n <= c)
- 기본 케이스 c(= Θ(1))
- 그렇지 않으면, 각각 원본의 1/b 크기의 하위 문제로 나눈다고 가정해 보자. (병합 정렬에서는 a=b=2)
- D(n)가 크기-n 문제를 나누는 시간
- 각 크기 n/b에 대해 해결해야 할 하위 문제가 있음
- 각 하위 문제를 푸는 데 T(n/b)이 걸림
- C(n)가 솔루션을 결합하는 시간이 되도록 함
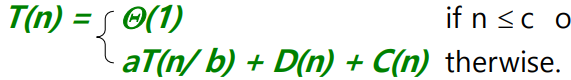
Merge sort 분석 - 반복 사용
-
n = 2^k 가정
-
기본 케이스: n = 1일 때, T(n) = 1
-
n >= 2인 경우 병합 정렬 단계의 시간
- 나눗셈: q를 p와 r의 평균으로 계산 -> D(n)=θ(1)
- 정복자: 두 개의 하위 문제를 각각 크기 n/2씩 반복적으로 해결함 -> 2T(n/2)
- 결합: 요소 하위 배열의 MERGE에는 θ(n) 시간이 걸림 -> θ C(n)=θ(n)
- D(n)+C(n)=θ(1)+θ(n)=θ(n)이므로 병합 정렬의 반복 실행 시간은
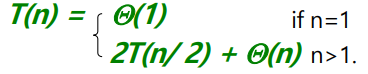
-
병합-결합 반복 해결: T(n) = π(n log2 n)
-
c는 기본 케이스의 T(n)와 분할 및 정복 단계에 대한 배열 요소당 시간의 상수
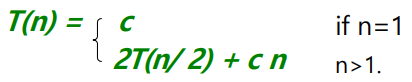
-
반복 트리를 그림, 이 트리는 반복의 연속적인 확장을 보여줌

정렬 알고리즘
- Binary Search
- Selection sort
- Bubble sort
- Horner's rule

