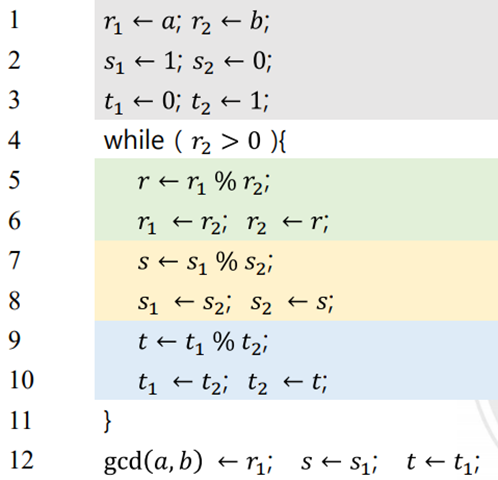[TIL]230309 - 컴퓨터시스템보안 2주차: 암호수학 - 기초정수론

기본 수 체계

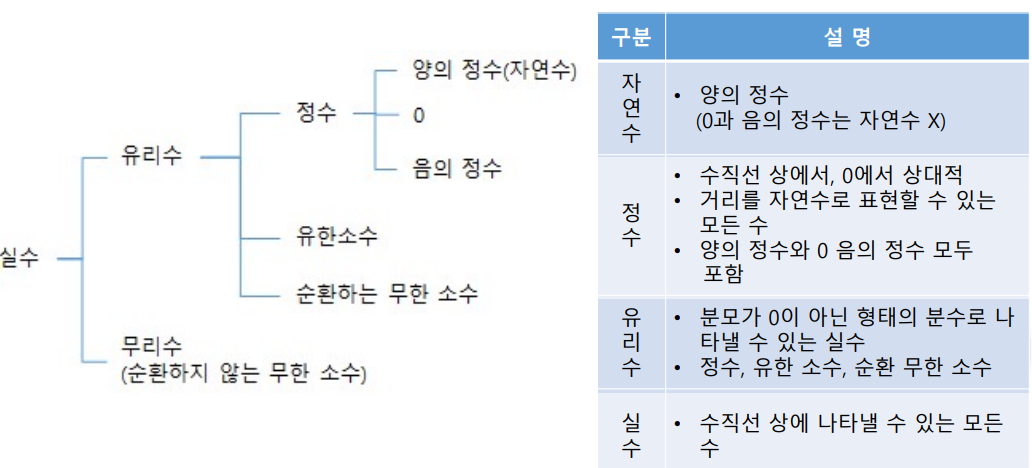
ex) 자연수는 0, 1, 2, 3, ... 과 같은 수이다. (x)

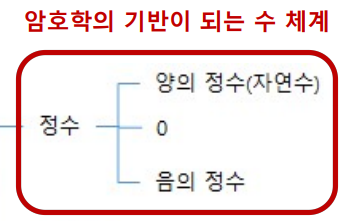
자연수: N
정수: Z
유리수: Q
실수: R

항등원과 역원

항등원 (Identity element)

• 임의의 원소 x에 특정 연산을 수행했을 때, x가 나오게 하는 원소 y
  1. 덧셈, 뺄셈 연산에 대한 항등원 -> 0 (x+y=x, x-y=x)
  2. 곱셈, 나눗셈 연산에 대한 항등원 -> 1 (x*y=x, x/y=x)

역원 (Inverse element)

• 임의의 원소 x에 특정 연산을 수행했을 때, 해당 연산의 항등원이 나오게 하는 원소 y
  1. 덧셈 연산에 대한 역원 -> -x (x+y=0, x-y=0)
  2. 곱셈 연산에 대한 역원 -> 1/x (x*y=1, x/y=1)

정수 집합

• 개수: ∞
• Z = {-∞, ..., -2, -1, 0, 1, 2, ..., ∞}
• a, b ∈ Z: 임의의 두 정수 a, b를 의미

이항 연산

• 두 입력 값으로부터 하나의 결과 값을 산출하는 연산
  

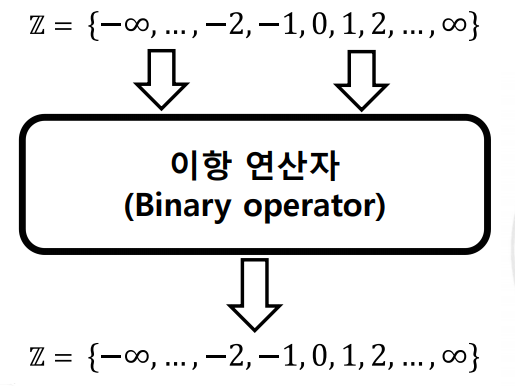
덧셈, 뺄셈, 곱셈, 나눗셈은 이항연산이다 (x)

• 나눗셈은 연산 결과로 몫과 나머지를 산출하므로, 이항연산에 속하지 않음 (출력값이 2개임)

나눗셈

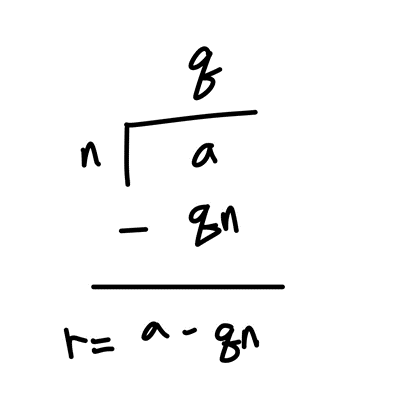
나눗셈 관계식
a = qn + r
q: 몫, n: 제수, a: 피제수 r: 나머지

제한 사항
1. n > 0
2. r >= 0

• 나눗셈은 상기의 등식으로 성립된다.
• 따라서, 나눗셈은 이항 연산이 아닌 관계식이다

나눗셈 정리

• 임의의 두 정수 a, b ∈ Z (b > 0)가 존재한다면, a = qb + r을 만족하는 두 정수 q, r ∈ Z이 항상 유일하게 존재함

가분성

• 나눌 수 있는 성질
• a를 n으로 나눌 때, 나머지가 0이라면, (즉, a = qn + r에서 r = 0)
  • n 은 a의 약수이다.
  • a는 n으로 나눌 수 있다.

• a를 n으로 나눌 때, 나머지가 0이 아니라면, (즉, a = qn + r에서 r > 0)
  • n은 a의 약수가 아니다.
  • a는 n으로 나눌 수 없다.'

가분성의 주요 성질

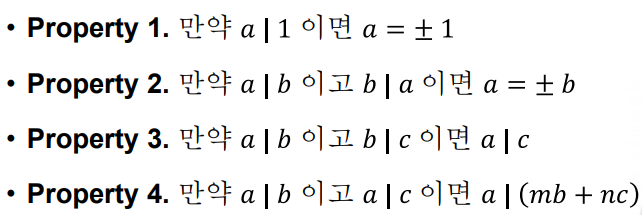
약수와 최대공약수

약수(Divisor)

• 양의 정수는 하나 이상의 약수를 갖는다.
• 약수의 성질
  • 정수 1은 하나의 약수, 즉 1만 가진다.
  • 모든 양의 정수는 최소 2개 이상의 약수(1과 자기 자신)를 가진다.

최대 공약수(GCD)

• 공약수: 두 양의 정수가 갖는 공통의 약수
• 최대 공약수
  • 두 양의 정수의 공약수 중에서 가장 큰 정수
  • 두 양의 정수의 최대 공약수 = 두 정수를 나누는 가장 큰 정수

140과 12의 최대 공약수 -> gcd(140, 12) = 4
(공약수: 1, 2, 4)

유클리드 알고리즘

• 두 양의 정수의 최대 공약수를 찾는 알고리즘
• 약 2000년 전에 수학자 유클리드가 고안
• 기본 원리
  • gcd(a, 0) = a
  • gcd(a, b) = gcd(b, r) where r = a를 b로 나눈 나머지

나머지도 동일한 최대 공약수를 가짐, a와 b의 최대공약수 g를 구하는 것은 b와 r의 최대공약수를 구하는 것과 동일함

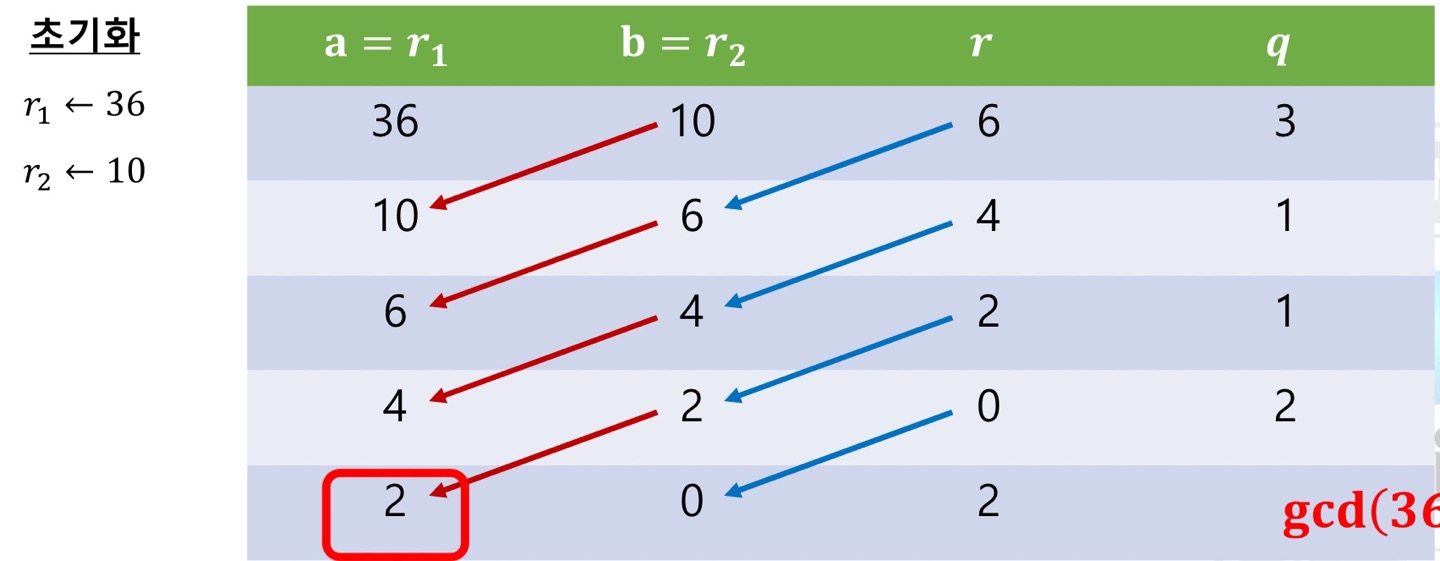
예제) 36과 10의 최대공약수를 유클리드 알고리즘으로 계산해라

gcd(36, 10) = 2

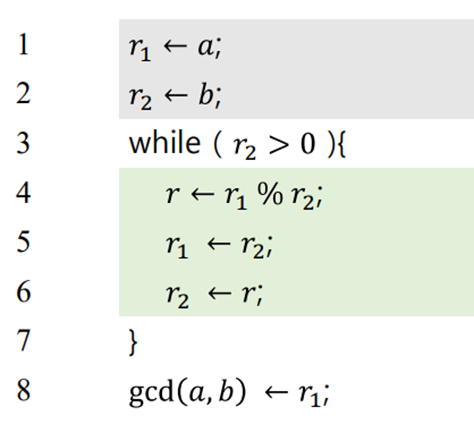
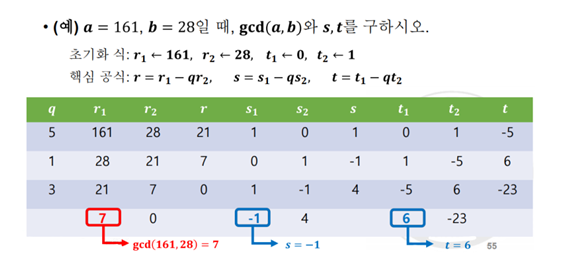
확장 유클리드 알고리즘

• 두 개의 정수 a와 b가 주어졌을 때, gcd(a, b)와 함께 다음을 만족하는 다른 두 정수 s와 t를 동시에 계산한다.
  • sa + tb = gcd(a, b)
• 핵심 공식: r = r1 - qr2, s = s1 - qs2, t = t1 - qt2
• 초기화식: r1 = a, r2 = b, t1 = 0, t2 = 1, s1 = 1, s2 = 0