RNN

1. 개요

1.1. Sequential Data

• Sequence of word
  • 이미지 캡션 자동 생성
  • 문장 번역
  • 단어 구분
• Sequence of balance
  • 기업 부도 예측

1.2. Deep Learning Dealing with Sequential Data

• MLP : 가중치가 고정되어 있음
  • 임의의 길이 seq를 다루지 못한다
  • seq 길이 맞추는 과정에서 정보손실 or 변형
  • 필요 파라미터가 많음
• CNN : 다변수 input & output 가능
  • RNN과 결합하여 사용하기도

2. RNN의 핵심 아이디어

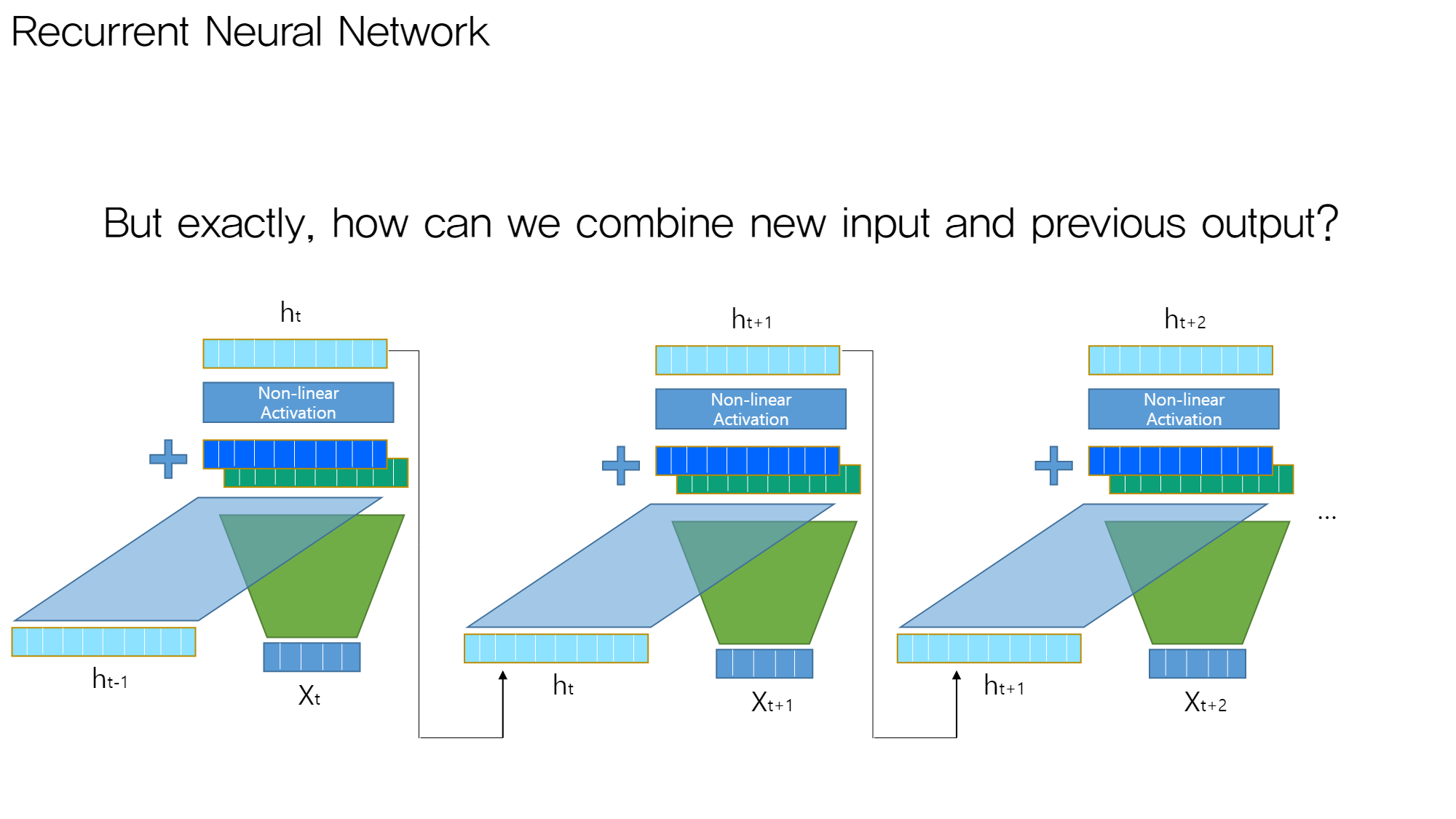
새로운 input과 이전 output을 같이 고려하자!

• How can we combine new input and previous output

  • 입력값 (new input, previous output)들을 각 가중치 행렬과 곱한다.
  • 두 연산 결과를 더한다

3. Task 유형

input 개수와 output 개수로 유형을 구별한다

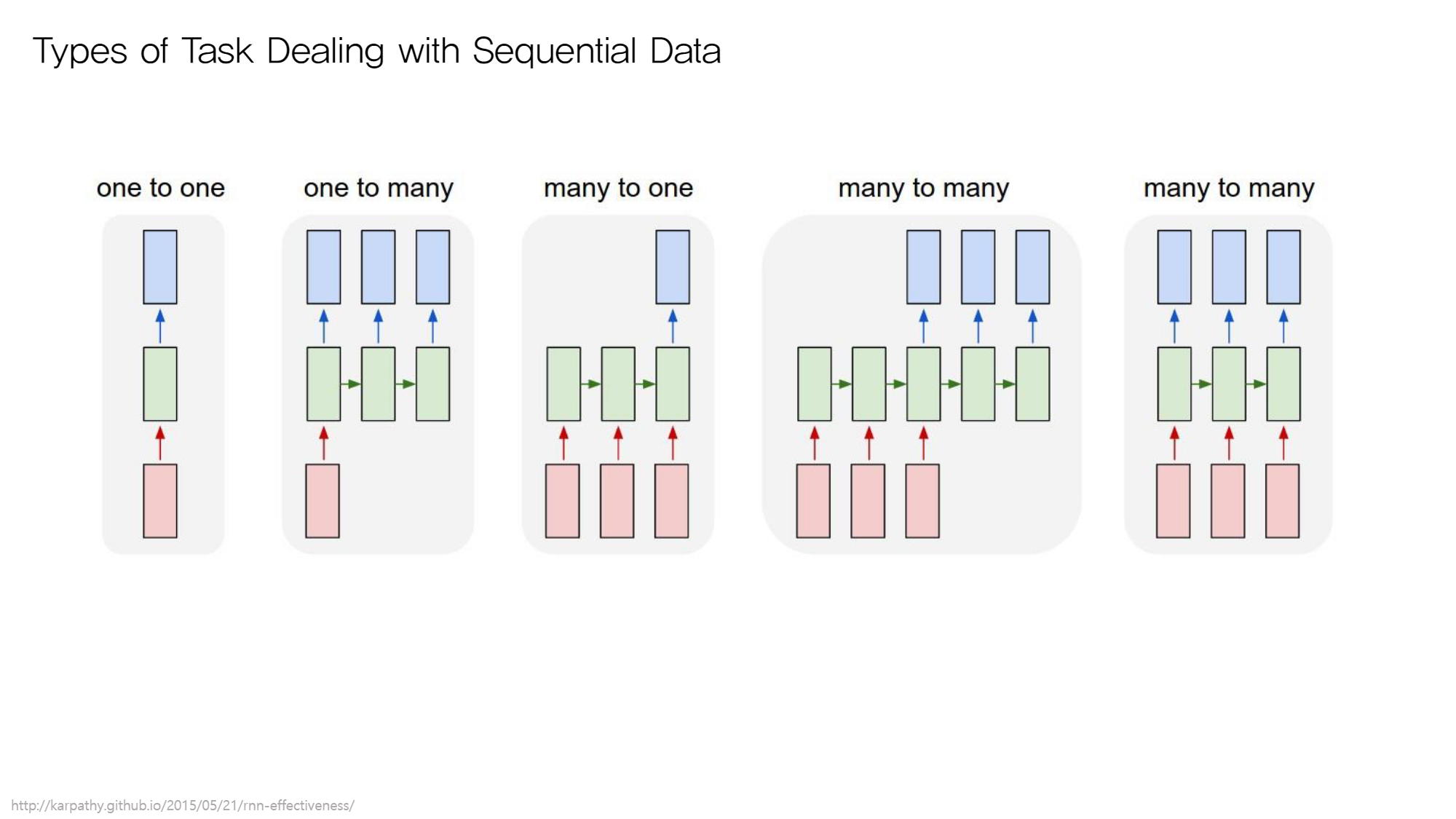
3.1. one to one

e.g. Translate one word into another language

3.2. one to many

하나의 이미지에서 여러 개의 feature 인식

e.g. Predict whether a company would be bankrupted

3.3. many to one

여러 개의 feature 보고 하나의 결과 예측

e.g. Automatically generate caption with the given image

→ 하나의 결과 = 망한다/안망한다

3.4. many to many (1)

단어들 집합 input & 단어들 집합 output

e.g. Translate one sentence into another language

3.5. many to many (2)

e.g. Classify whether the word is owns’ name or not (문장을 구성하는 각 단어를 품사로 구별 후 반환)

• output에 따른 구분
  • one : 마지막 input이 입력된 시점에서 output이 나옴
  • many : 각 time step에서 output이 나옴

4. 유형별 모델 구조

4.1. one to many

이전 단계의 output과 hidden state를 고려한다

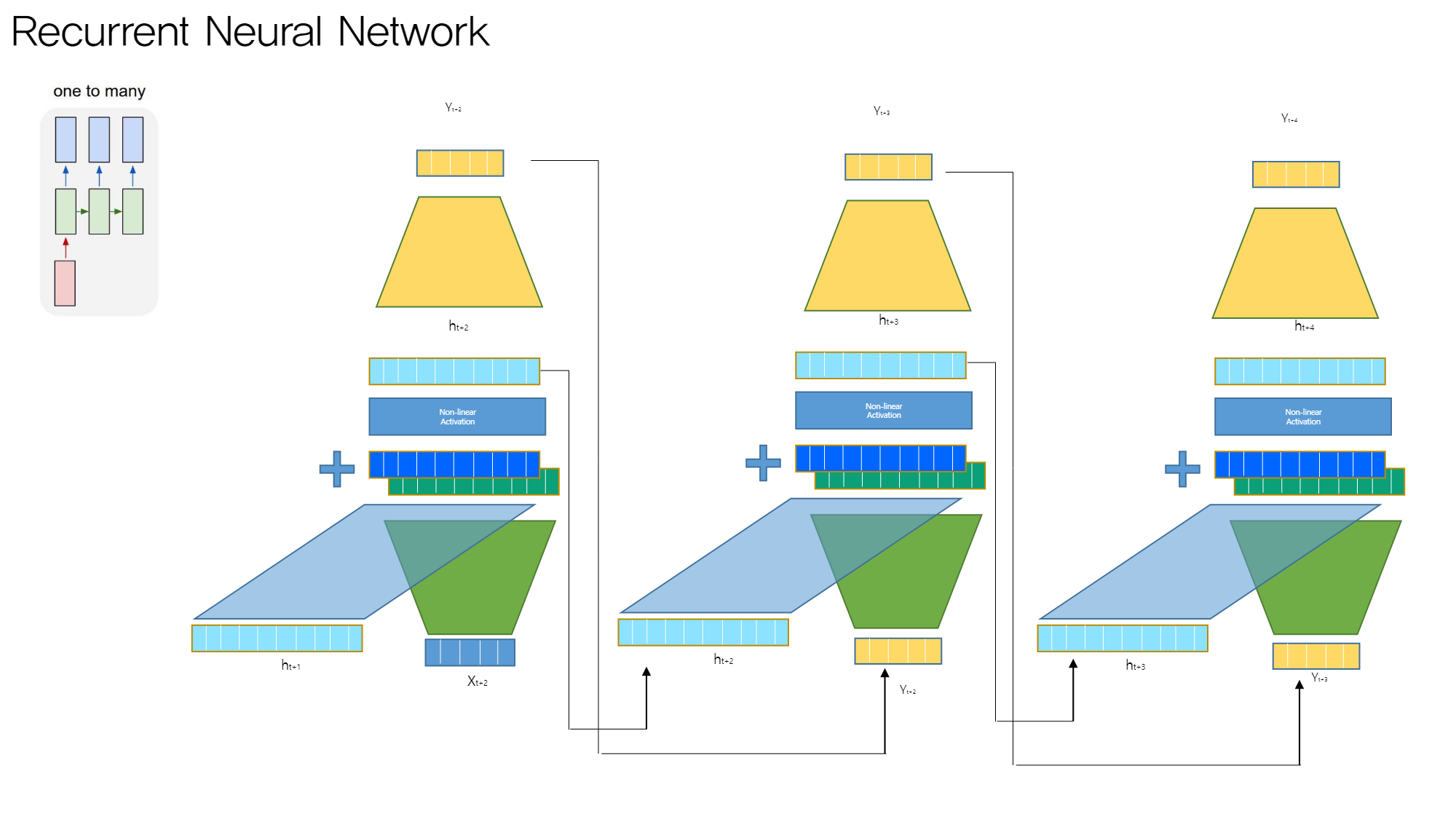
• 첫 단계에만 input data가 입력된다 (이미지 캡션 task의 경우: 인코딩된 이미지 벡터가 input data)
  
• 각 단계의 hidden state에 다른 모델 붙여서 output값 출력 → 다음 단계의 input data가 된다
  

4.2. many to one

기본 구조는 바닐라와 유사하다

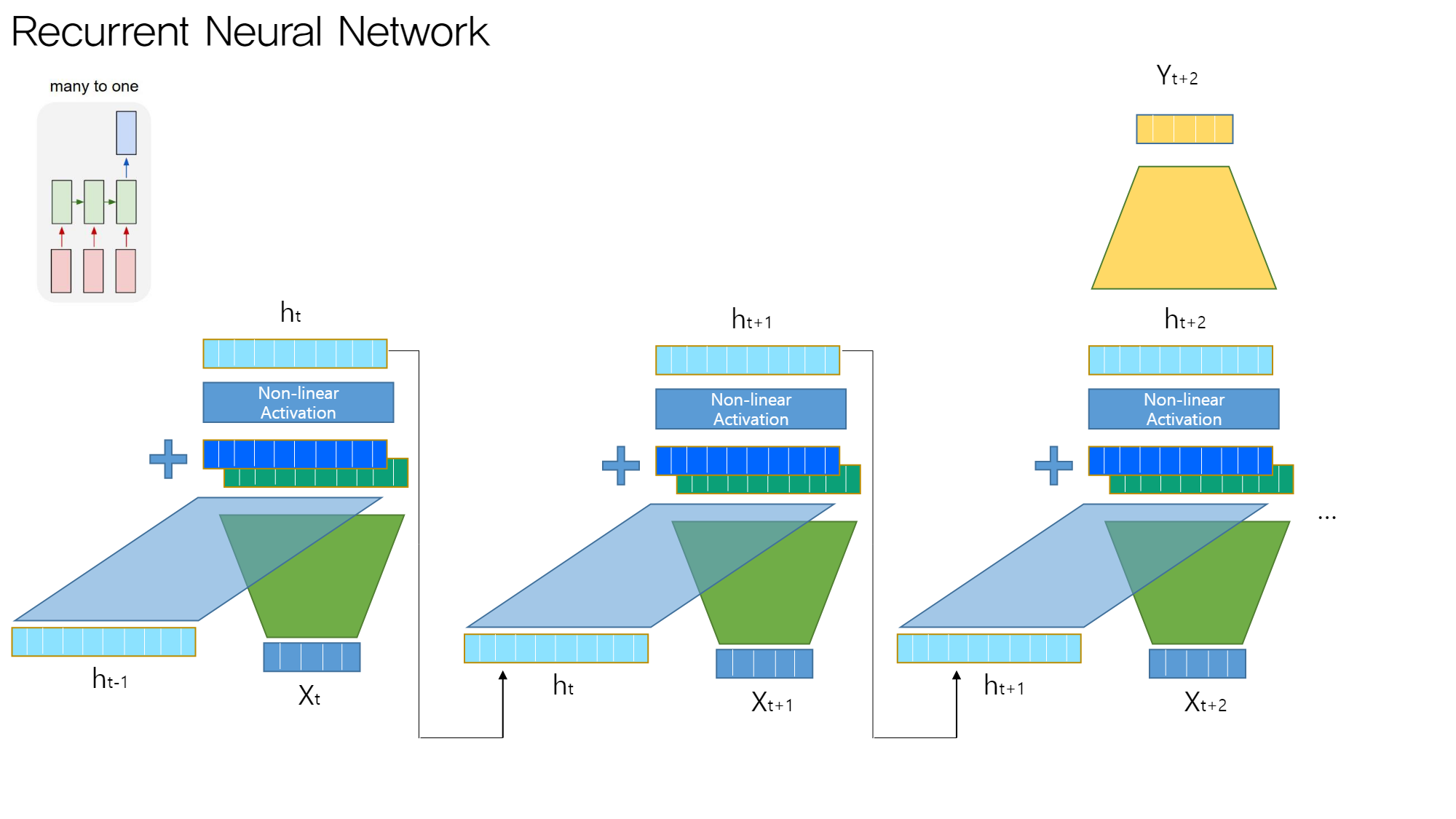
• 최종 hidden state는 sequence에 대한 요약 → 마지막 h에 원하는 모델을 붙인다.
  

many to many (1)

encoding과 decoding 과정을 구별하여 task를 수행한다

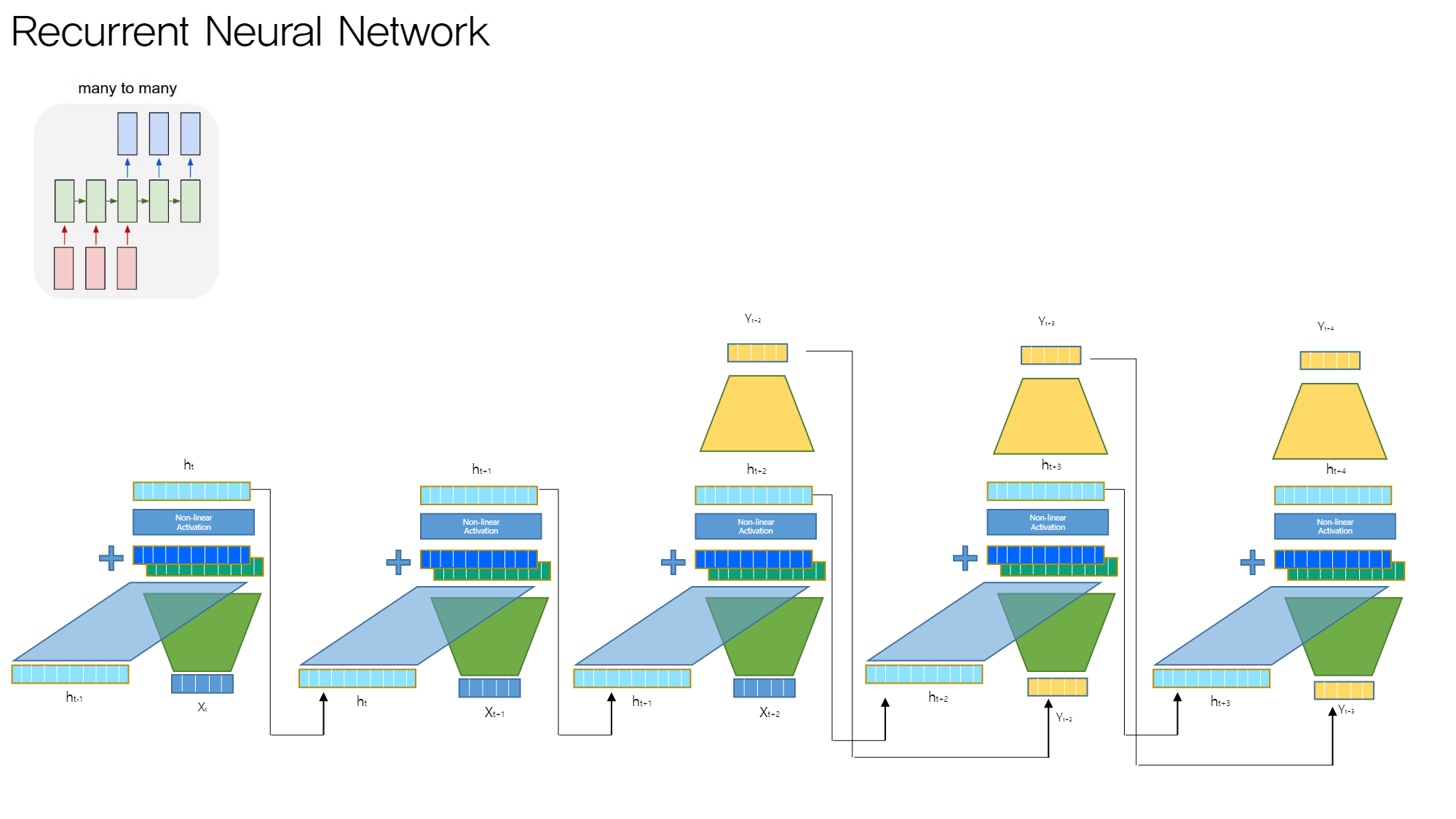
1. encoding
   • 마지막 input 입력 단계까지 ( 해당 단계 hidden state 구할 때까지 )
2. decoding
   • y를 generate하는 과정
3. encoding vs decoding
   • 일반적으로 파라미터 구별
   • 각 모델은 다른 것으로 취급
   • 통용되는 feature vector 존재

many to many (2)

각 time step마다 output을 출력한다

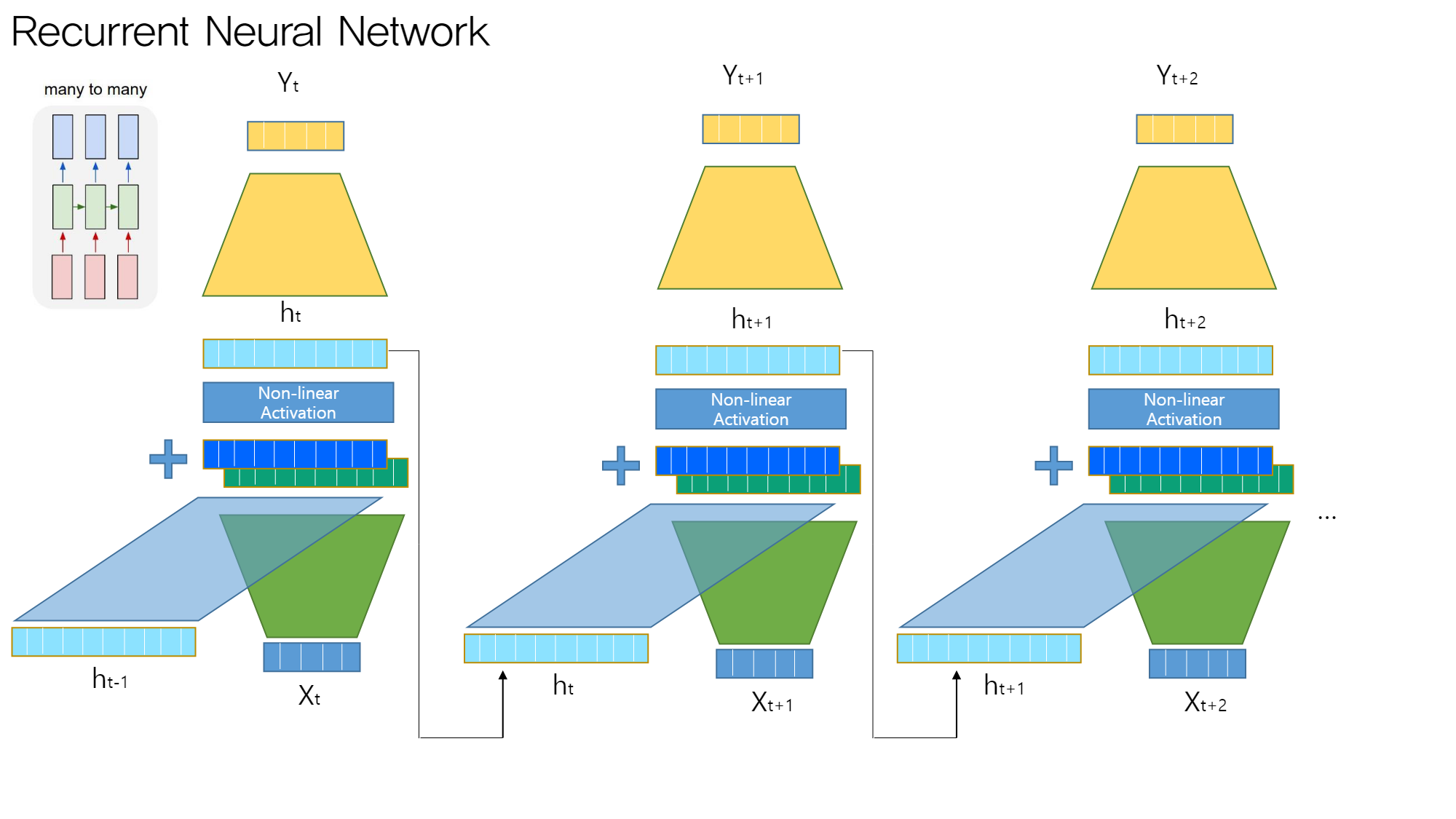
• 단계별 hidden state에 모델 추가 → 각 모델은 모두 동일하며 파라미터를 공유한다
  

4. 수식

바닐라 모델의 수식 구조

• $h_{t} = f(Ux_{t} + Wh_{t-1})$
  • $f(x) = tanh(x)$ : RNN에서 사용하는 비선형-활성화 함수
  • $Ux_{t}$ : input data와 가중치 행렬의 곱
  • $Wh_{t-1}$ : 이전 단계 hidden state와 가중치 행렬의 곱
• $y_{t} = f(Vh_{t})$
  • $f(x) = x$ (또는 MLP 사용하기도)

5. 모델 평가

$Loss(\theta) = \sum\limits_{t}loss(y_{true,t},y_{pred,t})$

• 각 pred-output 값에 대해 loss 도출 (학습 데이터의 true 값과 비교)
• Task에 따라 loss 식 다르게
  • Classification → CrossEntropy
  • Regression → MSE
• Sequence 별로 계산하여 평균 : 해당 loss를 backward 후 파라미터에 반영

6. 결론

6.1. 요약

1. RNN은 sequential data를 다루기 위한 알고리즘이다
2. 이전 output과 현재 input을 모두 고려한다
3. task에 따라 RNN 활용법이 달라진다

6.2. 한계

backward할 때 각 단계 non-linear activation 식을 여러번 거치면 grad가 0으로 수렴할 수 있다 : 학습이 잘 안되는 문제 발생

→ 이 한계를 극복한 방식이 LSTM!!

참고 & 이미지 출처 : 2019 KAIST 딥러닝 홀로서기 세미나