자료구조

시간복잡도와 공간복잡도

O(n) 수식(n)이 클수록 시간이 복잡해진다.

function decode(input):
	create output string
    for each letter in input
    	get new_letter from letter's location in cipher
        add new_letter to output
    return out put

• create return 2번 n번도는 for문안에 실행되는 코드가 2번있으니 2n + 2다.
• ciper의 데이터 형태에 따라 알파벳 list라면 29n+2만큼의 숫자다.
  허나 이정도는 O(n)이라고 한다. n의 제곱보다는 훨 작기때문이다.
  또 평균 값이 있는데 알파벳은 13이 평균이기에 16n+2로 줄어들 가능성이 크다.

인풋을 받고 인풋의 글자 수 만큼 for문을 돌고 해당하는 글자에 대응하는 문법(언어적) change한다.

2n 3n등의 수를 대부분 n 으로 통일한다.
1, 2, 3정도의 상수도 대략으로 개산하기에 1로 한다.

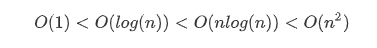
만큼의 순서를 가진다.

array

• 삽입하기에 어렵다. index단위이기에 개수가 늘수록 삽입할때 뒤의 많은양의 데이터가 뒤로 가야하므로 하나만으로도 worst case의 경우 O(n)의 시간이 걸릴 수도 있다.
• 삭제하기 역시 마찬가지다.

이를 위해서 Linked list다.

linked list

체인과 비유할 수 있다. 삽입과 삭제가 사슬처럼 연결되어있다. 그래서 길이와 위치를 알 필요가 없다.

• index 없이 value만으로 이루어져있음. 그리고 next를 포함하고 있어서
  인덱스 없이 알아서 다음 값으로 넘어감. 메모리 주소가 바로 붙어있어서 넘어가는 것임. c언어의 기본 배열은 linked list인듯. 기본 속도가 있긴한데 O(n)만큼만 이동하면 모든 값에 접근, 수정 가능

Dubled linked List 도 있다.

stack

• 최근 element에 관심 있을 때 유용
  다른 것을 찾을 필요 없이 가장 최근의 내용을 바로 볼 수 있기에

push는 element를 추가하고 pop으로 꺼내온다.
시간 복잡도는 O(1)만큼 든다.

value와 next만 있다. 역순으로 next가 작동.

L.I.F.O.

Last in, First Out 나중에 들어온 것이 가장 먼저 나간다.

queue

시간 복잡도 O(1)만큼 든다.

F.I.F.O.

먼저 들어온게 먼저 나간다 head와 tail로 tail이 가장 최근의 요소.
enqueue dequeue 는 tail로 들어오고 head로 나간다.
peek는 head를 뜻한다.

deque . 덱

스택과 큐의 합.
둘의 특성을 가능함
앞뒤로 넣고 앞뒤로 뺄 수 있음.

priority Queue

순서를 정한 큐 우선순위를 정한다 우선순위가 같을경우 먼저 들어온 애가 나간다.

set

• 순서도 중복값도 없고 오직 하나씩만 존재한다. 기존 set과 동일.

map

• dict와 유사하다. key값이 하나만 존재한다 = set. value는 여러가지가 있다 하더라도 key값은 오직 하나다.

• key는 map에서 유일해야한다.
  map =
  

hash function

constant time만 필요.

list set stack queue는 모두 linear time이 필요하다.

어떤 값을 저장하거나 꺼내쓰기 용이하게 만든다.
hash function은 어떠한 식? 조건?으로 해당 식을 통과하여 나온 값으로 value를 얻을 수 있다. 암호화와 유사한 느낌.
그래서 constant time만 걸린다.

하지만 다른 input 에서 같은 hash value가 나오는 경우가 있다 이는 collision이라 불린다.
그럴때는 hash function을 수정해서 더 많은 slot을 가지게 하는 것이다.
또는 list로 연결해서 순서로 찾거나 하면 된다. 시간이 조금 더걸리지만 그래도 속도가 빨라진다.

• 하지만 메모리가 꽤 필요한 경우가 있다. 메모리 복잡도가 증가할 경우가 있다 (collision의 경우)
  key는 변경 불가(unique)여야한다. key가 변경가능하면 value가 계속 달라지기때문에.
  그래서 튜플과 문자열만 올 수 있다.

  bucket 은 collision의 경우
  최악의 경우 linear time만큼 걸릴 수도 있다 전부 bucket 에 들어가는 경우.

  다른 방법

  hash f후 또 hash f을 하는 것이다. 이러면 bucket이 작아진다.
  그리고 해쉬가 가능한 경우(변경불가)만 가능! 튜플과 문자열등의 경우

  만약 문자열의 경우는 아스키코드를 이용할 수 있다.
  s[m]*31^(n-l) 31인 이유는 아마 32부터 아스키코드가 사용가능하기 때문인듯.

  sorted array

  해당 배열 에서는 정렬되어있으므로 중간부터 검사한다 up down게임 생각하기
  원래였다면 O(n)에서 최악의 경우 조차 절반정도로 줄어든다.
  n이 클수록 점점 더 효율이 좋다.
  n / 2번째 인덱스만 계속 계산하기. 중간보다 크면 우측 작으면 좌측만 가져오기.

  len(arr)이 1이면 그만하면 됌.
  array sizwe가 double이 될때 iteration(반복)의 수가 증가

  결국 O(log2(n) + 1) = O(log(n))만큼 걸린다. n은 입력갯수

  linear search #선형 서치

  binary search #절반씩 계산하는 서치

  버블정렬

  앞부터 두개씩 묶어서 값비교 좌측이 우측보다 크면 서로 자리 바꿈
  O((n-1)^2)만큼의 효율성 = O(n^2).
  사실상 n-2만큼만 해도 되고 덜 걸리게 셋팅할 수 있다.(마지막 자리를 점점 줄여도 괜찮음(for문 돌때마다 뒤부터 값 고정)
  wor case = O(n^2)
  aver case = O(n^2)
  best case = O(n) 이미 정리된 경우

  Merge sort : efficiency

  그룹을 나누어서 계산 그룹끼리도 계산.

  O(n log(n)) 정도의 복잡도

  quick 정렬

  우측부터 자리가 작으면 바꾸는 정렬 하나만 잡고 계속 검사

  O(n log(n)) 정도의 복잡도

  trees

  하나 아래에 여러 개를 가지고 있다.
  linked list의 확장개념 개개인은 노드라고 불림.
  next는 가리킬 수 있는 다른 노드.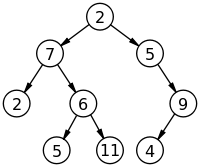

  
  출처: 위키백과
  트리는 사이클 구조면 안된다(자기 자신에게 돌아오면 안된다.)
  자기 아래의 노드는 자식노드 자기 위의 노드는 부모노드다.

  더이상 자식이 없는 5 11 4부분을 leaf라고 부른다.
  height는 노드 층의 계수로 현재 최대 층수는 3층이기에 height는 3이다.
  depth는 height의 반대로 생각하면 된다 leaf는 depth가 3이다.
  트리의 경우는 순서가 중요하기에 순서를 정해줘야 한다.
  깊이위주로(자식-손자..., 자식-손자...) 할 지
  너비위주(자식들-손자들...)로 할 지가 중요하다

  DFS(깊이우선탐색)와 BFS(너비우선탐색)

  
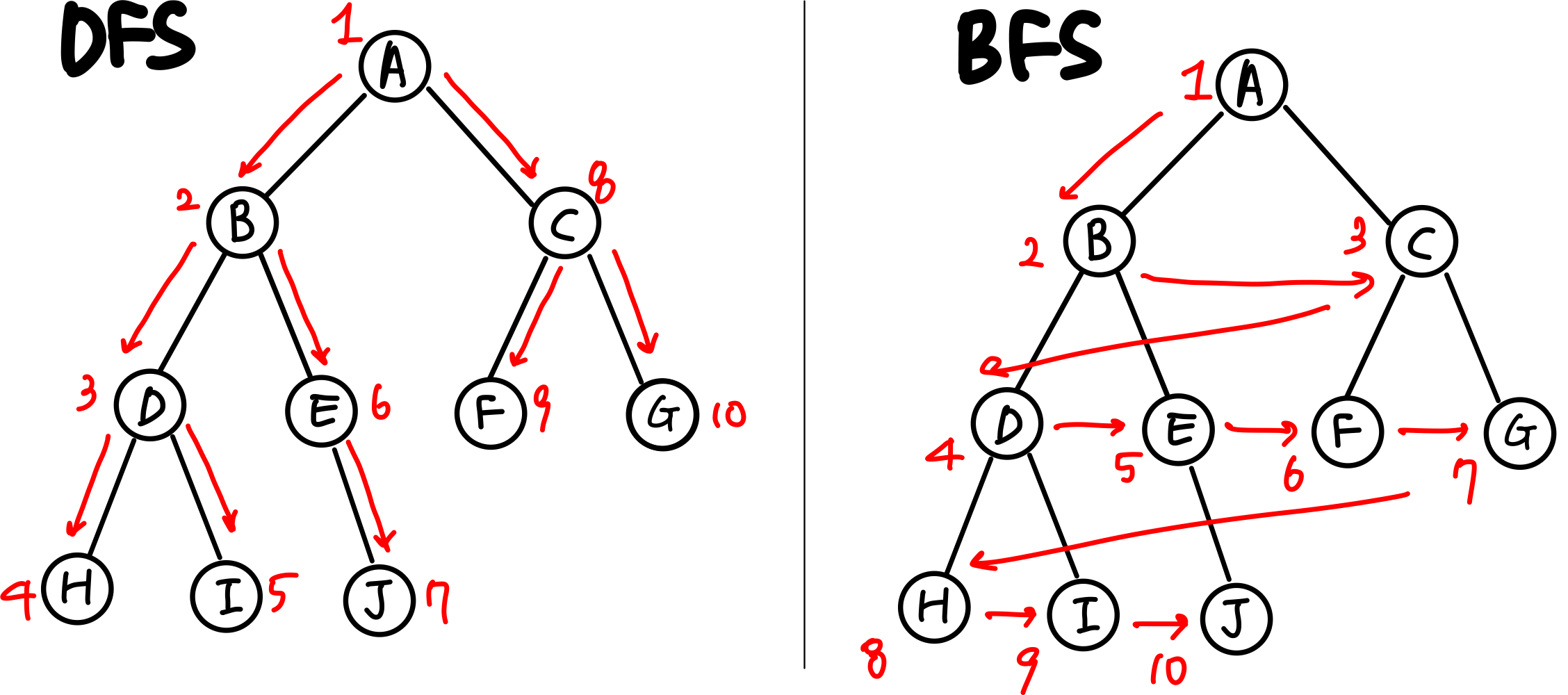
  *출처 백준 코딩테스트
  해당 자료가 DFS와 BFS를 설명하기 가장 편하다.

  DFS

  Pre-order 방식은 A-B-D-H-I-J... 이런 순으로 한자녀부터 끝까지 내려갔다 올라와서 다시 내려간다.

  in-order 방식은 아래서부터 올라갔다 내려갔다 올라갔다 하는 방식
  H-D-I-B-E-J.... 부모로가서 부모의 다른 자식으로 간다.
  간단히 왼쪽에서 오른쪽으로 간다.

  post-order 방식은 부모가 나중인 방식으로 H-I-D-J-E-B-F-G-C-A 이런 순서다.
  부모노드의 자식노드를 먼저 찾는 방식이다.

  BFS

  Binary Tree는 자녀가 두개거나 하나거나 없거나의 경우를 만족하면 된다.

  Search and Delete

• O(n)만큼의 시간복잡도를 가진다.

• 삭제를 할때에는 연결을 해줘야 트리 방식을 유지할 수 있다. 허나 자식이 많이 딸린 경우의 delete에서는 애매해지기에 자식 중 한 명을 부모노드로 옮기는 방식이 있다.

• 거기에 손주까지 붙어있으면 손주도 승진해야하고 자신도 승진해야해서 점점더 오래 걸린다.

  insert

  insertion은 간단하다 부모노드만 정하면 된다.
  시간복잡도는 아무리 해봐야 O(height)정도다.

  ####perfect trees
  빈 공간이 없으며 노트 개수가 1, 3, 7... 의 식으로 2의 승을 더해나간 값이 나오는 경우를 perfect trees라고 한다.

Binary Search Tree

root보다 큰건 우측 작은건 좌측으로 정렬하는 경우를 말한다.
값비교를 통해서 원하는 값을 찾기 용이하다.
O(log(n))의 시간복잡도로 원하는 값을 찾을 수 있다.
insert를 하기에도 좋다. 해당 값이 들어가기 좋은 위치를 바로 찾을 수 있기에.
unbalanced의 경우가 worst case다 O(n)이 되는 경우

빅오 표기법

시간(또는 공간)복잡도를 나타냄.
연산횟수가 무엇이든 차수가 가장 큰 항만 남긴다. 앞에붙은 m도 지우고 O(n^3)으로만 남긴다.