Personalization 관련 논문을 읽으면서 기본 아키텍쳐와 Diffusion 기본 개념에 대해 무지한게 느껴져 기초가 되는 DDPM을 읽고 이해해보기로 했습니다.
공부한 내용은 하단의 링크에 모아두었고 이해한 내용을 바탕으로 흐름을 정리해보았습니다.
본격적으로 들어가기 전에 사전지식입니다.
Variational Inference
Markov Chain
Bayes rule
KL divergence
VAE
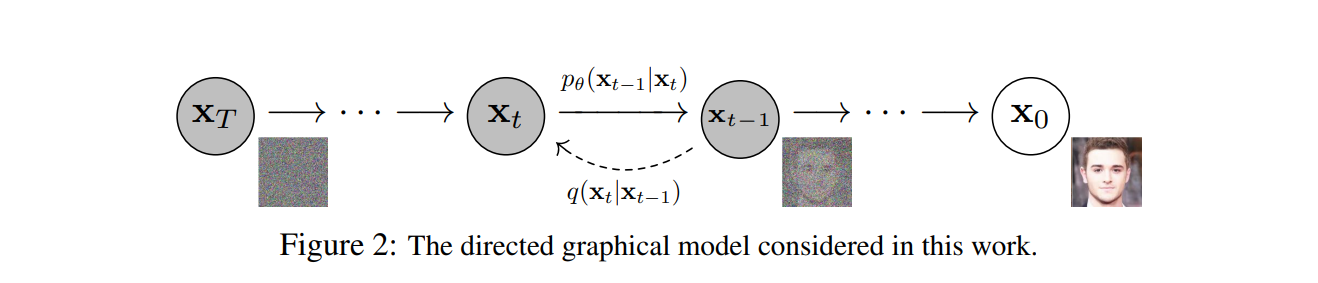
Diffusion process는 2015 ICML의 unsupervised learning using nonequilibrium thermodynamics 논문이 시초입니다. 연기가 퍼지는 과정을 아주 짧은 시간동안 관찰하면 그 연기는 가우시안 분포를 따라 퍼집니다. 그리고 그 반대의 과정도 가우시안 분포라고 할 수 있습니다. 이미지에 noise를 추가하고 제거하는 것도 이와 동일한 과정으로 보고 diffusion model이 나오게 되었습니다.
Model Architecture
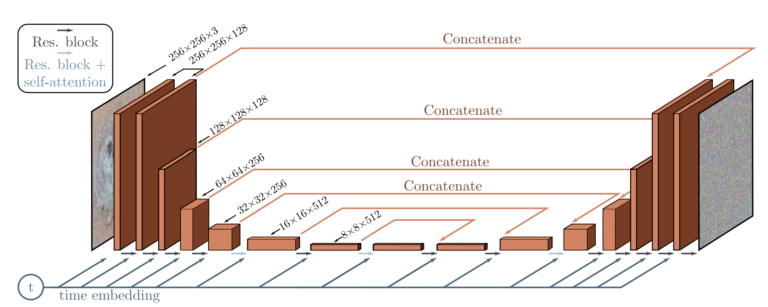
시작하기에 앞서 Model Architecture를 먼저 살펴보겠습니다.
Unet을 사용하며 각 layer에 time step t를 추가적으로 넣어주는 것을 볼 수 있습니다.X t X_{t} X t X t − 1 X_{t-1} X t − 1
Forward Process
forward 프로세스는 가우시안(정확히 conditional gaussian)이므로 아래와 같이 표현가능합니다. 식은 N ( 0 , I ) \mathcal{N}(0, I) N ( 0 , I )
q ( X t ∣ X t − 1 ) = N ( X t ; μ t − 1 , Σ t − 1 ) = N ( X t ; 1 − β t X t − 1 , β t I ) \begin{aligned} q(X_{t}|X_{t-1}) &= \mathcal{N}(X_{t};\mu_{t-1},\,\Sigma_{t-1})\\ &= \mathcal{N}(X_{t};\sqrt{1-\beta_{t}}X_{t-1},\,\beta_{t}I) \end{aligned} q ( X t ∣ X t − 1 ) = N ( X t ; μ t − 1 , Σ t − 1 ) = N ( X t ; 1 − β t X t − 1 , β t I )
아래식을 보면 timestep이 크다는 가정하에 V a r ( X t − 1 ) = 1 , V a r ( ϵ ) = 1 Var(X_{t-1})=1,\,Var(\epsilon)=1 V a r ( X t − 1 ) = 1 , V a r ( ϵ ) = 1
V a r ( X t ) = V a r ( 1 − β t X t − 1 + β t ϵ ) = ( 1 − β t ) V a r ( X t − 1 ) + β t V a r ( ϵ ) = 1 − β t + β t = 1 \begin{aligned} Var(X_{t})&=Var(\sqrt{1-\beta_{t}}X_{t-1}+\sqrt{\beta_{t}}\epsilon)\\ &=(1-\beta_{t})Var(X_{t-1})+\beta_{t}Var(\epsilon)\\ &=1-\beta_{t}+\beta_{t}\\ &=1 \end{aligned} V a r ( X t ) = V a r ( 1 − β t X t − 1 + β t ϵ ) = ( 1 − β t ) V a r ( X t − 1 ) + β t V a r ( ϵ ) = 1 − β t + β t = 1
N ( X t ; 1 − β t X t − 1 , β t I ) \mathcal{N}(X_{t};\sqrt{1-\beta_{t}}X_{t-1},\,\beta_{t}I) N ( X t ; 1 − β t X t − 1 , β t I ) X t X_{t} X t
X t = 1 − β t X t − 1 + β t ϵ X_{t}=\sqrt{1-\beta_{t}}X_{t-1}+\sqrt{\beta_{t}}\epsilon X t = 1 − β t X t − 1 + β t ϵ timestep t일때의 이미지를 한번씩 더해가면서 구하는게 아니라 한번만에 구할 수 있습니다.
α t = 1 − β t , a t ~ = ∏ i = 1 T α i q ( X t ∣ X 0 ) = N ( X t ; a t ~ X 0 , ( 1 − a t ~ ) I ) \alpha_{t}=1-\beta_{t},\,\tilde{a_{t}}=\prod_{i=1}^T\alpha_{i}\\ q(X_{t}|X_{0})=\mathcal{N}(X_{t};\sqrt{\tilde{a_{t}}}X_{0},\,(1-\tilde{a_{t}})I) α t = 1 − β t , a t ~ = i = 1 ∏ T α i q ( X t ∣ X 0 ) = N ( X t ; a t ~ X 0 , ( 1 − a t ~ ) I )
x t = 1 − β t x t − 1 + β t ϵ t − 1 ϵ t − 1 ∼ N ( 0 , I ) = α t x t − 1 + 1 − α t ϵ t − 1 = α t ( α t − 1 x t − 2 + 1 − α t − 1 ϵ t − 2 ) + 1 − α t ϵ t − 1 ϵ t − 2 ∼ N ( 0 , I ) = α t α t − 1 x t − 2 + α t ( 1 − α t − 1 ) ϵ t − 2 + 1 − α t ϵ t − 1 \begin{aligned} x_{t}&=\sqrt{1-\beta_{t}}x_{t-1}+\sqrt{\beta_{t}}\epsilon_{t-1}\quad\epsilon_{t-1} \sim \mathcal{N}(0, I)\\ &=\sqrt{\alpha_{t}}x_{t-1}+\sqrt{1-\alpha_{t}}\epsilon_{t-1}\\ &=\sqrt{\alpha_{t}}(\sqrt{\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t-1}}\epsilon_{t-2})+\sqrt{1-\alpha_{t}}\epsilon_{t-1}\quad\epsilon_{t-2} \sim \mathcal{N}(0, I)\\ &=\sqrt{\alpha_{t}\alpha_{t-1}}x_{t-2}+\sqrt{\alpha_{t}(1-\alpha_{t-1})}\epsilon_{t-2}+\sqrt{1-\alpha_{t}}\epsilon_{t-1} \end{aligned} x t = 1 − β t x t − 1 + β t ϵ t − 1 ϵ t − 1 ∼ N ( 0 , I ) = α t x t − 1 + 1 − α t ϵ t − 1 = α t ( α t − 1 x t − 2 + 1 − α t − 1 ϵ t − 2 ) + 1 − α t ϵ t − 1 ϵ t − 2 ∼ N ( 0 , I ) = α t α t − 1 x t − 2 + α t ( 1 − α t − 1 ) ϵ t − 2 + 1 − α t ϵ t − 1 α t ( 1 − α t − 1 ) ϵ t − 2 + 1 − α t ϵ t − 1 ∼ N ( 0 , ( 1 − α t α t − 1 ) I ) \sqrt{\alpha_{t}(1-\alpha_{t-1})}\epsilon_{t-2}+\sqrt{1-\alpha_{t}}\epsilon_{t-1}\sim \mathcal{N}(0,\,(1-\alpha_{t}\alpha_{t-1})I) α t ( 1 − α t − 1 ) ϵ t − 2 + 1 − α t ϵ t − 1 ∼ N ( 0 , ( 1 − α t α t − 1 ) I )
= α t α t − 1 x t − 2 + 1 − α t α t − 1 ϵ t − 2 ′ ϵ t − 2 ′ ∼ N ( 0 , I ) = α t α t − 1 α t − 2 x t − 3 + 1 − α t α t − 1 α t − 2 ϵ t − 3 ′ ϵ t − 3 ′ ∼ N ( 0 , I ) = . . . = α t ~ x 0 + 1 − α t ~ ϵ 0 ′ ϵ 0 ′ ∼ N ( 0 , I ) \begin{aligned} &=\sqrt{\alpha_{t}\alpha_{t-1}}x_{t-2}+\sqrt{1-\alpha_{t}\alpha_{t-1}}\epsilon'_{t-2}\quad \epsilon'_{t-2} \sim \mathcal{N}(0, I)\\ &=\sqrt{\alpha_{t}\alpha_{t-1}\alpha_{t-2}}x_{t-3}+\sqrt{1-\alpha_{t}\alpha_{t-1}\alpha_{t-2}}\epsilon'_{t-3}\quad \epsilon'_{t-3} \sim \mathcal{N}(0, I)\\ &=...\\ &=\sqrt{\tilde{\alpha_{t}}}x_{0}+\sqrt{1-\tilde{\alpha_{t}}}\epsilon'_{0} \quad \epsilon'_{0} \sim \mathcal{N}(0, I) \end{aligned} = α t α t − 1 x t − 2 + 1 − α t α t − 1 ϵ t − 2 ′ ϵ t − 2 ′ ∼ N ( 0 , I ) = α t α t − 1 α t − 2 x t − 3 + 1 − α t α t − 1 α t − 2 ϵ t − 3 ′ ϵ t − 3 ′ ∼ N ( 0 , I ) = . . . = α t ~ x 0 + 1 − α t ~ ϵ 0 ′ ϵ 0 ′ ∼ N ( 0 , I )
N ( X t ; a t ~ X 0 , ( 1 − a t ~ ) I ) \mathcal{N}(X_{t};\sqrt{\tilde{a_{t}}}X_{0},\,(1-\tilde{a_{t}})I) N ( X t ; a t ~ X 0 , ( 1 − a t ~ ) I )
X t = α t ~ X 0 + ( 1 − α t ~ ) ϵ X_{t}=\sqrt{\tilde{\alpha_{t}}}X_{0}+\sqrt{(1-\tilde{\alpha_{t}})}\epsilon X t = α t ~ X 0 + ( 1 − α t ~ ) ϵ 그럼 이제 여기까지 X 0 X_{0} X 0 X t X_{t} X t β \beta β (학습가능하기도 하다) 로 설정했기 때문에 learnable variable은 없다는 것을 보았습니다.
Reverse Process
Forward Process의 역과정인 Reverse Process는 Forward 과정과 유사합니다. DDPM의 핵심이기도 한 이 과정은 P θ P_{\theta} P θ q q q
P θ ( X t − 1 ∣ X t ) = N ( X t − 1 ; μ θ ( X t , t ) , Σ θ ( X t , t ) ) P_{\theta}(X_{t-1}|X_{t})=\mathcal{N}(X_{t-1};\mu_{\theta}(X_{t},\,t),\,\Sigma_{\theta}(X_{t},\,t)) P θ ( X t − 1 ∣ X t ) = N ( X t − 1 ; μ θ ( X t , t ) , Σ θ ( X t , t ) ) DDPM에서 분산은 time step t에 의존하는 변수이므로 아래와 같이 표현됩니다.
P θ ( X t − 1 ∣ X t ) = N ( X t − 1 ; μ θ ( X t , t ) , σ t 2 I ) P_{\theta}(X_{t-1}|X_{t})=\mathcal{N}(X_{t-1};\mu_{\theta}(X_{t},\,t),\,\sigma_{t}^{2}I) P θ ( X t − 1 ∣ X t ) = N ( X t − 1 ; μ θ ( X t , t ) , σ t 2 I ) 이제 이 과정에서 학습해야할 건 μ θ \mu_{\theta} μ θ
DDPM Loss
VAE와 DDPM은 결국 NLL을 통해서 구하는데 그 전개 방식도 유사합니다. 그럼 먼저 VAE먼저 유도하면서 DDPM으로 넘어가겠습니다. 기존 VAE에서는 l o g P θ logP_{\theta} l o g P θ
VAE loss
E z ∼ q ( z ∣ x ) [ − l o g P θ ( x ) ] = ∫ − l o g P θ ( x ) ⋅ q ( z ∣ x ) d z ∵ D e f i n i t i o n o f E = ∫ − l o g P θ ( x , z ) P θ ( z ∣ x ) q ( z ∣ x ) d z = ∫ ( − l o g P θ ( x , z ) P θ ( z ∣ x ) ⋅ q ( z ∣ x ) q ( z ∣ x ) ) ⋅ q ( z ∣ x ) d z = ∫ − l o g P θ ( x , z ) q ( z ∣ x ) ⋅ q ( z ∣ x ) d z + ∫ − l o g q ( z ∣ x ) P θ ( z ∣ x ) ⋅ q ( z ∣ x ) d z = − E L B O − K L ( q ( z ∣ x ) ∣ ∣ P θ ( z ∣ x ) ) ∵ K L ≥ 0 ≤ ∫ − l o g P θ ( x , z ) q ( z ∣ x ) ⋅ q ( z ∣ x ) d z = ∫ − l o g P θ ( x ∣ z ) P θ ( z ) q ( z ∣ x ) ⋅ q ( z ∣ x ) d z \begin{aligned} \mathbb{E_{z\sim q(z|x)}}[-logP_{\theta}(x)]&=\int{-logP_{\theta}(x)}\cdot q(z|x)dz\quad\because Definition\,of\, \mathbb{E}\\ &=\int{-log{{P_{\theta}(x, z)}\over P_{\theta}(z|x)}} q(z|x)dz\\ &=\int(-log{{{P_{\theta}(x, z)}\over{P_{\theta}(z|x)}}\cdot{{{q(z|x)}\over{q(z|x)}}}})\cdot q(z|x)dz\\ &=\int{-log{{P_{\theta}(x, z)}\over{q(z|x)}}\cdot q(z|x)}dz+\int{-log{{q(z|x)}\over{P_{\theta}(z|x)}}}\cdot q(z|x)dz\\ &=-ELBO-KL(q(z|x)||P_{\theta}(z|x))\quad\because KL \ge 0\\ &\leq \int{-log{{P_{\theta}(x, z)}\over{q(z|x)}}\cdot q(z|x)}dz\\ &=\int{-log{{{P_{\theta}(x|z)P_{\theta}(z)}\over{q(z|x)}}}\cdot q(z|x)dz} \end{aligned} E z ∼ q ( z ∣ x ) [ − l o g P θ ( x ) ] = ∫ − l o g P θ ( x ) ⋅ q ( z ∣ x ) d z ∵ D e f i n i t i o n o f E = ∫ − l o g P θ ( z ∣ x ) P θ ( x , z ) q ( z ∣ x ) d z = ∫ ( − l o g P θ ( z ∣ x ) P θ ( x , z ) ⋅ q ( z ∣ x ) q ( z ∣ x ) ) ⋅ q ( z ∣ x ) d z = ∫ − l o g q ( z ∣ x ) P θ ( x , z ) ⋅ q ( z ∣ x ) d z + ∫ − l o g P θ ( z ∣ x ) q ( z ∣ x ) ⋅ q ( z ∣ x ) d z = − E L B O − K L ( q ( z ∣ x ) ∣ ∣ P θ ( z ∣ x ) ) ∵ K L ≥ 0 ≤ ∫ − l o g q ( z ∣ x ) P θ ( x , z ) ⋅ q ( z ∣ x ) d z = ∫ − l o g q ( z ∣ x ) P θ ( x ∣ z ) P θ ( z ) ⋅ q ( z ∣ x ) d z 여기서 P θ ( z ) P_{\theta}(z) P θ ( z ) q ( z ∣ x ) q(z|x) q ( z ∣ x ) P θ ( x ∣ z ) P_{\theta}(x|z) P θ ( x ∣ z ) q ( z ∣ x ) q(z|x) q ( z ∣ x )
VAE to DDPM
VAE에서는 latent가 z이지만 DDPM에서는 x T x_{T} x T
∫ − l o g P θ ( x ∣ z ) P θ ( z ) q ( z ∣ x ) ⋅ q ( z ∣ x ) d z = ∫ − l o g P θ ( x ∣ z ) q ( z ∣ x ) ⋅ q ( z ∣ x ) d z + ∫ − l o g ( P θ ( z ) ) ⋅ q ( z ∣ x ) d z = E x T ∼ q ( x T ∣ x 0 ) [ − l o g P θ ( x 0 ∣ x T ) q ( x T ∣ x 0 ) ] + E x T ∼ q ( x T ∣ x 0 ) [ − l o g P θ ( x T ) ] = − K L ( q ( x T ∣ x 0 ) ∣ ∣ P θ ( x 0 ∣ x T ) ) + E x T ∼ q ( x T ∣ x 0 ) [ − l o g P θ ( x T ) ] \int{-log{{{P_{\theta}(x|z)P_{\theta}(z)}\over{q(z|x)}}}\cdot q(z|x)dz}\\ =\int{-log{{{P_{\theta}(x|z)}\over{q(z|x)}}}\cdot q(z|x)dz} + \int{-log(P_{\theta}(z))\cdot q(z|x)dz}\\ =\mathbb{E_{x_{T}\sim q(x_{T}|x_{0})}}[-log{{{P_{\theta}(x_{0}|x_{T})}\over{q(x_{T}|x_{0})}}}] + \mathbb{E_{x_{T}\sim q(x_{T}|x_{0})}}[-logP_{\theta}(x_{T})]\\ =-KL(q(x_{T}|x_{0})||P_{\theta}(x_{0}|x_{T})) + \mathbb{E_{x_{T}\sim q(x_{T}|x_{0})}}[-logP_{\theta}(x_{T})] ∫ − l o g q ( z ∣ x ) P θ ( x ∣ z ) P θ ( z ) ⋅ q ( z ∣ x ) d z = ∫ − l o g q ( z ∣ x ) P θ ( x ∣ z ) ⋅ q ( z ∣ x ) d z + ∫ − l o g ( P θ ( z ) ) ⋅ q ( z ∣ x ) d z = E x T ∼ q ( x T ∣ x 0 ) [ − l o g q ( x T ∣ x 0 ) P θ ( x 0 ∣ x T ) ] + E x T ∼ q ( x T ∣ x 0 ) [ − l o g P θ ( x T ) ] = − K L ( q ( x T ∣ x 0 ) ∣ ∣ P θ ( x 0 ∣ x T ) ) + E x T ∼ q ( x T ∣ x 0 ) [ − l o g P θ ( x T ) ]
처음에 언급한 "P θ P_{\theta} P θ q q q q ( x T ∣ x 0 ) q(x_{T}|x_{0}) q ( x T ∣ x 0 ) P θ ( x 0 ∣ x T ) P_{\theta}(x_{0}|x_{T}) P θ ( x 0 ∣ x T )
길이 너무 길면 읽기 힘드니 여기까지 하고 나머지는 다음 포스팅에서 하도록 하겠습니다.
참고 링크
영상
블로그
논문