✏️ 세그먼트 트리
- 주어진 데이터의 구간 합과 데이터 업데이트를 빠르게 수행하기 위해 만들어진 자료구조의 형태
- 더 큰 범위는 인텍스 트리 라고 불리는데, 코테 영역에서는 큰 차이는 없다.
- 🔗 합배열 구하기
📍 핵심 이론
- 구간 합, 최대 값, 최소 값 구하기로 나눌 수 있다.
- 트리 초기화 하기 → 질의값 구하기 → 데이터 업데이트 하기 과정을 거저 구현된다.
📍 1. 트리 초기화 하기
- 트리를 초기화 하기 위해선 트리의 노드 수를 알아야 한다.
-
트리 배열의 크기는 아래의 공식으로 구할 수 있다.
// k 구하는 방법 2^k >= N // 트리 배열의 크기 구하는 방법 2^k * 2 -
예를들어 N 이 4 일 때 k 의 최소값이 2 이므로 배열의 크기는 8 이다.
-
N 이 5 ~ 8 일땐 k 의 최소값이 3 이므로 배열의 크기는 16 이다.
-
- 트리의 크기를 구했다면 원본 데이터를 트리 배열로 옮겨야 한다.
- 트리 배열의
2^k번 인덱스 부터 원본 인덱스를 복사해주면 된다. - 만약 원본 배열의 길이가 8 이라면,
트리 배열의 8번 인덱스 부터 원본배열을 순서대로 채워주면 된다.
- 트리 배열의
- 그 다음 인덱스를 2로 나눈 자리에 해당 인덱스의 값들을 더해준다.
- 만약 인덱스가 14 와 15 라면 둘 다 7번 인덱스를 가리키고, 7번 인덱스에 14번, 15번 인덱스의 합이 입력된다.
- 또 7번, 6번 인덱스는 3번 인덱스를 가리키고, 3번 인덱스는 7, 6 인덱스의 합이 입력된다.
- ⚠️ 참고로 0번 인덱스는 사용되지 않는다.
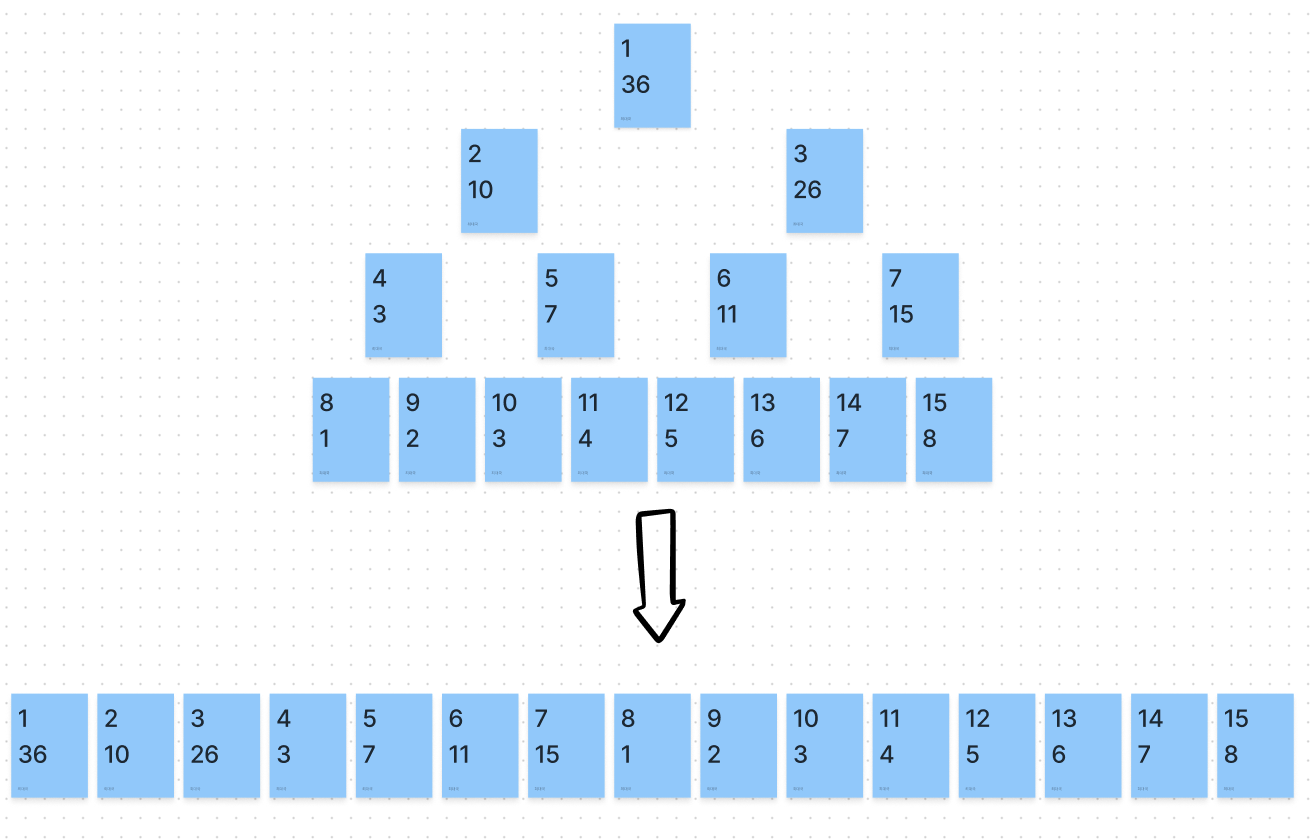
- 위와 같은 방식으로 구간의 합 뿐 아니라 구간의 최소값, 최대값 도 구할 수 있다.
📍 질의값 구하기
- 주어진 질의를 세그먼트 트리의 인덱스 번호로 바꾸려면 아래의 공식을 사용하면 된다.
index = 주어진 index + 2^k - 1- 위의 사진자료로 비교했을 때 1 ~ 3 의 구간 합을 구하기 위해선 아래와 같이 변경할 수 있다.
start = 1 + 8 - 1
end = 3 + 8 - 1 // 8 ~ 11 번 인덱스의 구간 합을 구하면 됨- 방금 예시처럼 부모노드가 딱 떨어질경우 문제가 없지만 부모노드가 딱 떨어지지 않을 때의 경우의 수도 고려해야 한다.
- 2 ~ 7 번 의 구간합을 구해야 할 경우를 예로 들면 아래와 같이 해결할 수 있다.
start = 2 + 7 // 9
end = 7 + 7 // 14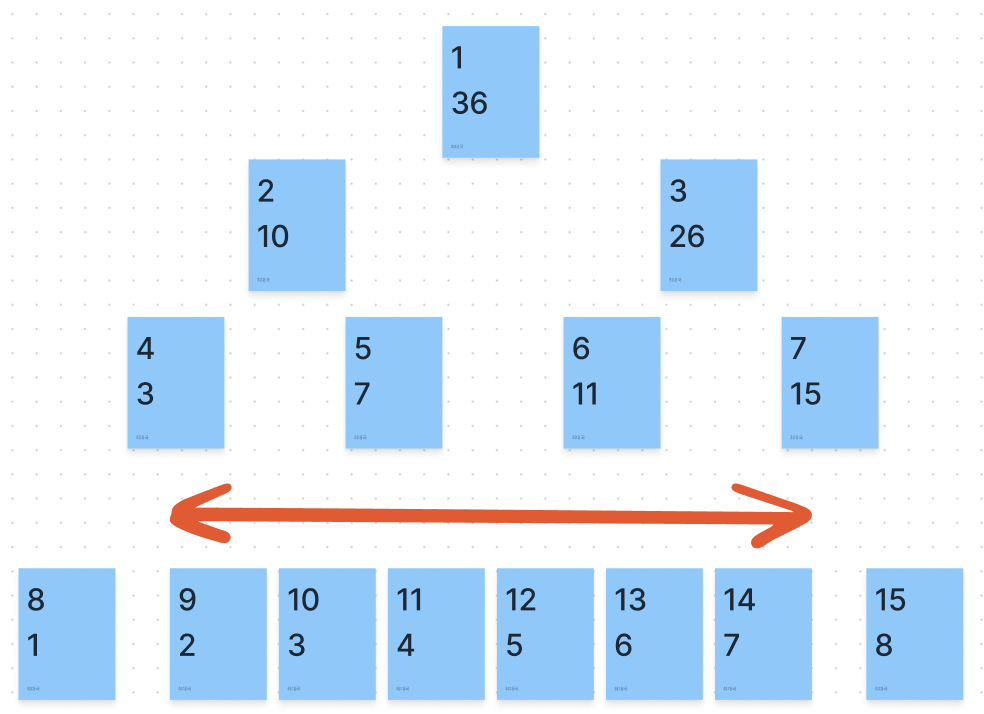
- 이런 경우 때문에 부모 노드로 이동할 때 아래와 같은 방식을 취한다.
// 딱 떨어지지 않는 값 변수로 저장하기
if (start / 2 == 1) start 인덱스 저장
if (end / 2 == 0) end 인덱스 저장
// 부모 노드로 이동하기
시작 부모 인덱스 = (start + 1) / 2
끝 부모 인덱스 = (end - 1) / 2- 위와 같은 과정을 거치면 아래와 같은 모습이 된다.
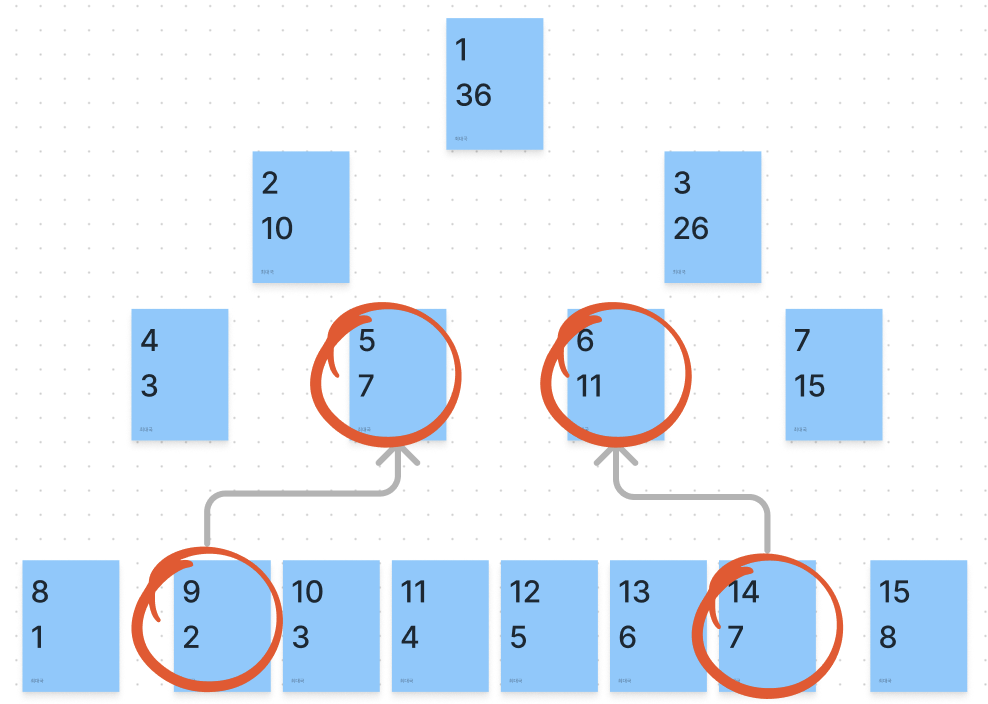
- 아래의 경우가 만족되지 않을 때 까지 위 작업을 반복한다.
while (start < end){
start = (start + 1) / 2
end = (end - 1) / 2
}- 결국 아래와 같이 start 와 end 의 값이 같아지거나, 크기가 뒤집히게 된다.
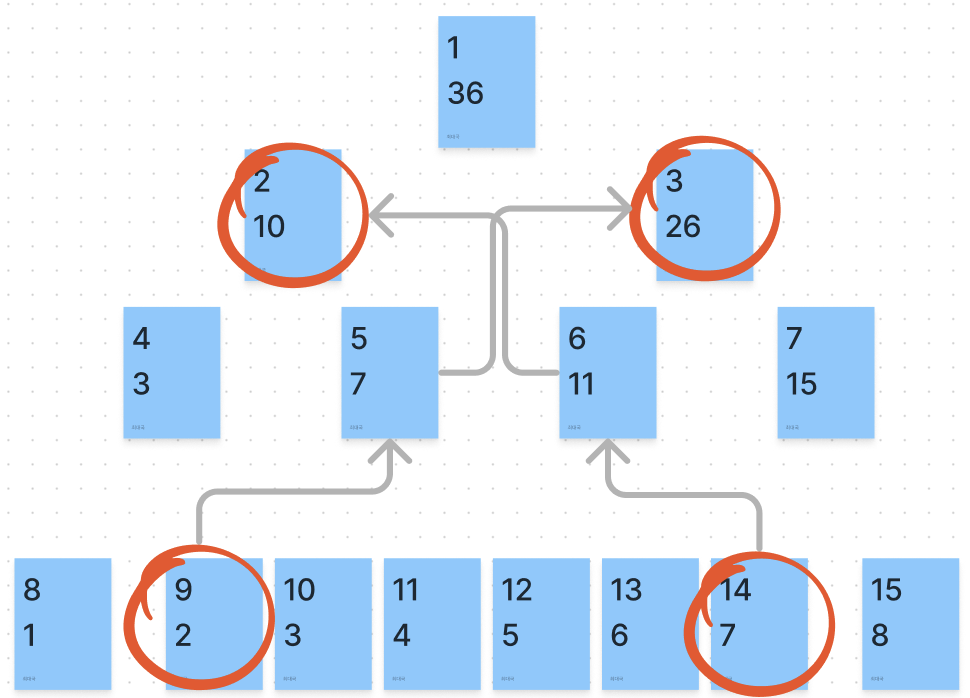
- 그럼 반복을 멈추고 값을 더해주면 된다.
📍 업데이트 하기
변경 인덱스 + 2^k - 1의 인덱스 값을 변경한 뒤 부모 node 로 올라가며 수정해주면 된다.
