✏️ DFS 란?
📍 기본 이론
- 그래프 완전 탐색 기법 중 하나이다.
- 그래프의 시작 노드에서 출발해 탑색할 한 쪽 분기를 정하여 최대 깊이까지 탐색을 마친 후,
다른 쪽 분기로 이동해 다시 탐색을 수행하는 알고리즘이다.
- DFS 는 후입 선출의 특성을 가지므로 재귀 함수 또는 Stack 을 이용해 구현할 수 있다.
- O(V + E) 의 시간복잡도를 가진다.
- V = 노드의 수
- E = 에지의 수
- 재귀 함수로 DFS 를 구현할 때 Stack Overflow 를 주의해야 한다.
- Stack Overflow 는 너무 많은 재귀가 반복될 때 발생되는 오류이다.
- DFS 를 활용하면
단절점 찾기 , 단절선 찾기, 사이클 찾기 , 위상 정렬 등을 사용할 수 있다.
📍 핵심 이론
- DFS 는 한번 방문했던 노드를 다시 방문하지 않는다.
- 따라서 노드의 방문여부를 체크할 배열이 필요하다.
- 그래프를 표현할 땐 인접 List 로 표현한다.
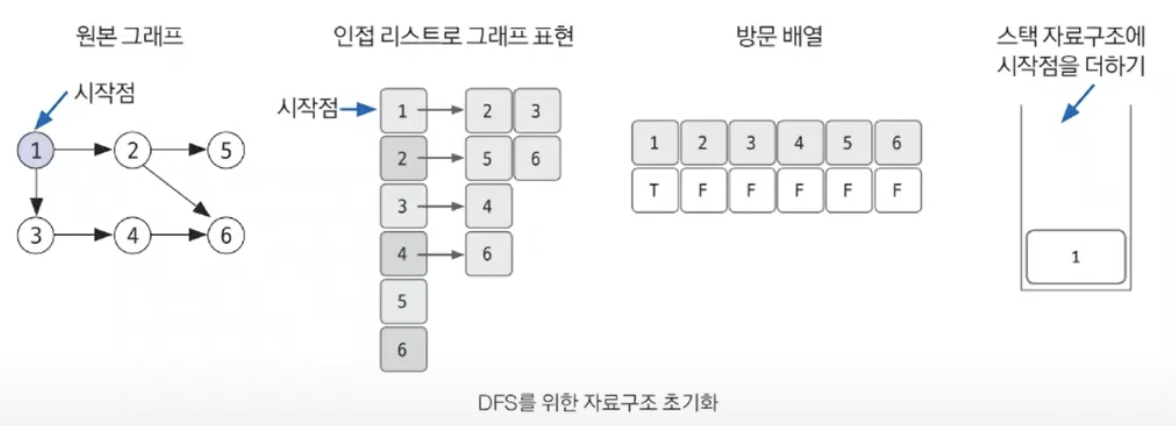
1. 시작할 노드를 정한 후 사용할 자료구조 초기화 하기
- 원본 그래프를 인접 리스트로 표현한다.
- 방문 배열을 초기화 한다.
- 시작 노드를 Stack 에 삽입 한다.
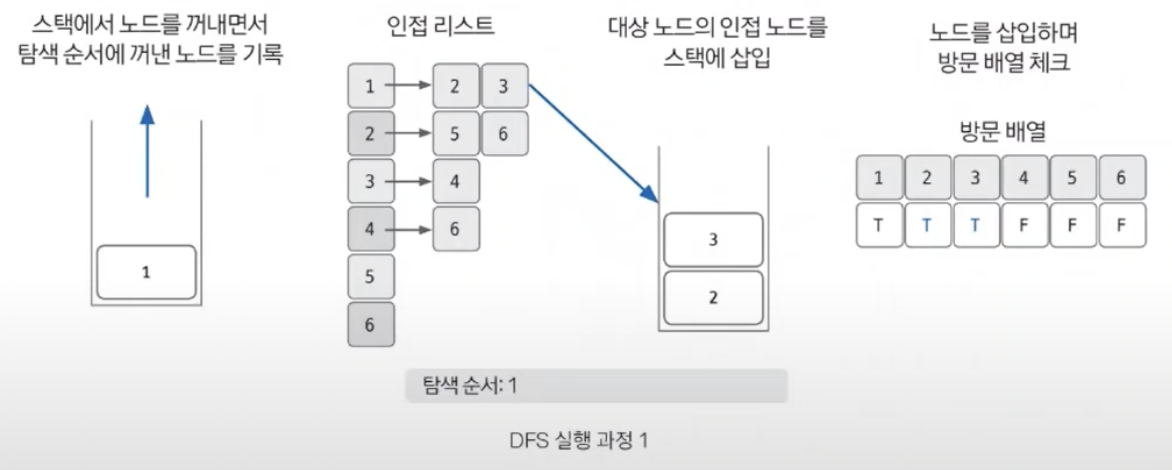
2. Stack 노드를 꺼낸 후 꺼낸 노드의 인접 노드를 다시 Stack 에 삽입
- Stack 에서 노드를 꺼내고, 탐색 순서에 꺼낸 노드를 기입한다.
- 인접 리스트의 인접 노드를 스택에 삽입해 방문 배열을 체크한다.
3. 1번 2번 반복하기
- Stack 에 값이 없을 때 까지 반복한다.
- 이 때 이미 다녀간 노드는 방문 배열을 참고해 다시 삽입되지 않도록 한다.1


