Knapsack

배낭(Knapsack) 혹은 가방 문제는 부분집합들 중 문제에서 제시하는 조건에 가장 알맞은(최적화) 부분집합을 찾는 문제다.
여기에선 그리디로 해결할 수 있는 'Fractional Knapsack Problem'처럼 짐을 쪼개는 문제가 아닌, 가방에 담을 수 있는 짐은 쪼개지 못하는 경우를 이야기한다.

그림출처:나무위키Knapsack 알고리즘 문제는 그림과 같이 가방 안에 무게를 초과하지 않으면서 담을 수 있는 최대한의 가치를 구하는 문제의 형태로 나타난다. 그래서 구할 수 있는 모든 부분집합 중에서 무게 15를 넘기지 않는 동시에 가장 높은 가치를 지니고 있는 부분집합을 정답으로 출력하면 된다.
하지만 부분집합을 구하기 위해 연산을 한다면 빅오 표기법에 따라 'O(2**N)'으로 지수 시간이 소요된다. 그리고 문제의 형식이 같은 짐을 한 개만 담을 수 있는지 아니면 무한정 담을 수 있는지, 가방이 한 개만 존재하는지 아니면 여러 개 존재하는지에 따라 해결을 해야 하는데, 그럴 경우 연산 횟수는 더욱 많아질 것이다. 그래서 대부분의 문제는 모든 부분집합 경우의 수를 구하게 되면 시간 초과로 오답처리가 될 확률이 매우 높다.

다이나믹 프로그래밍(DP)

다이나믹 프로그래밍의 문제풀이는 메모이제이션을 통해 같은 연산을 하지 않으며(시간 복잡도를 낮추고 공간 복잡도를 올려), 큰 문제를 아주 작은 문제로 쪼개서 점진적으로 해결(점화식을 통해)한다.
Knapsack 문제는 이렇게 DP를 활용하여 문제를 풀어갈 수 있다. 가방 무게 만큼의 리스트 배열을 생성하고 짐이 하나만 존재한다면 어떻게 담을 수 있는지 해결한 후 그 다음 두 개가 존재할 때 어떻게 담을지 해결하는 식으로 진행된다.

문제:

n개의 짐은 가치와 무게로 주어지며 짐들을 가방에 담을 때 가방의 무게는 m으로 주어질 때, 가방 무게를 초과하지 않으면서 담을 수 있는 최대한의 가치를 반환하시오.(n개의 짐은 각각 무한으로 주어져 있다고 가정한다)
n = 5, m = 15
1 1
2 2
2 1
10 4
4 12

풀이:

1.

가방에 넣을 수 있는 무게에 따른 가치를 각각의 짐을 통해 확인해보자.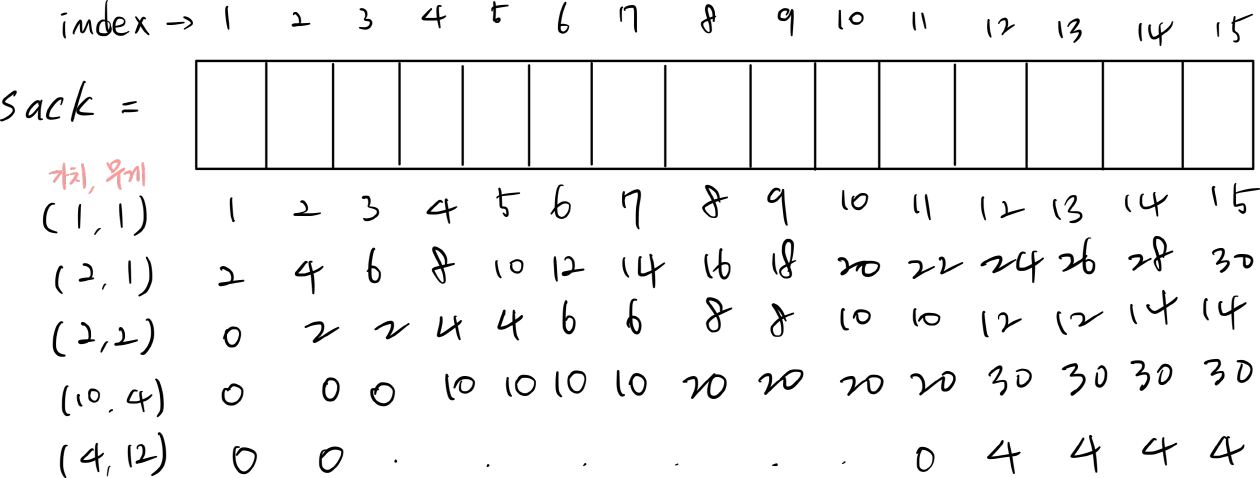인덱스를 무게로 설정하여 가방에 각각의 짐을 담은 경우의 가치는 위와 같다.

2.

하나의 짐을 담을 수 있는 경우를 다 확인하면 그 다음의 짐을 통해서 담을 수 있는 경우의 수를 확인하여 가방에 담을 수 있는 가치를 업데이트 한다.

3.

'현재의 가방 무게 = 짐을 넣기 전의 가방 무게 + 넣은 짐의 무게'

'현재의 가방 무게 = 짐을 넣기 전의 가방 무게 + 넣은 짐의 무게' 라는 것을 이용하여 짐을 넣기 전의 가치에 현재의 가치를 더하여 업데이트를 진행하는데, 만약 가치가 업데이트 되기 전의 가치보다 높다면 업데이트를 진행한다.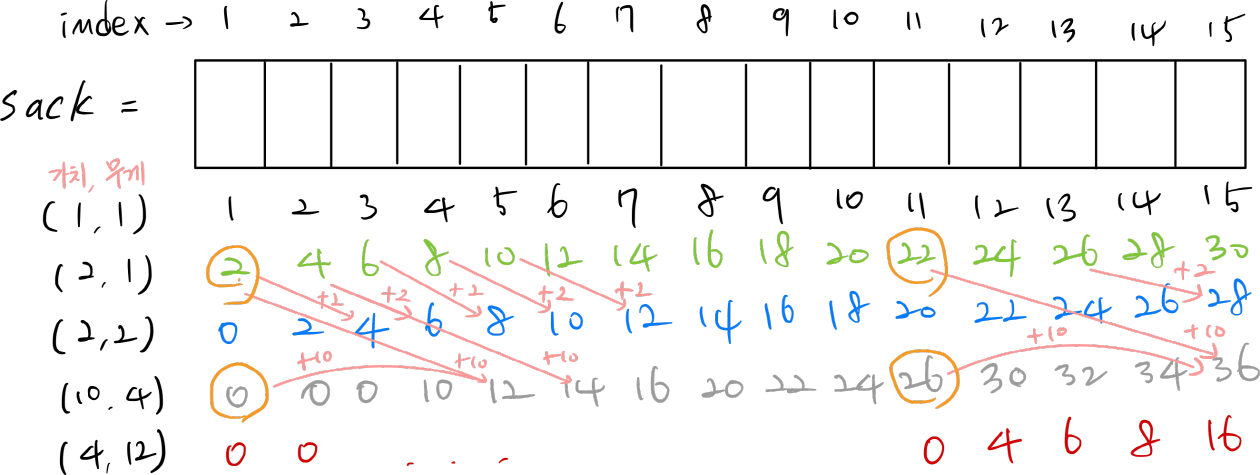
배열을 이용한 점진적인 업데이트를 통해 현재까지 가방의 무게가 최고의 가치로 업데이트 되어 있어서, 현재의 가치를 담는 것이 더 가치가 높다면 업데이트가 되고 아니면 업데이트 되지 않는다.

4.

모든 짐이 가방의 무게만큼 업데이트 되면 가방 15짜리의 가치는 최적의 업데이트가 된 상태이기에 인덱스 배열의 인덱스 15를 출력하면 된다.

코드:

입력:
5 15
1 1
2 2
2 1
10 4
4 12

def Knapsack(n, m):
    bag = [0] * (m + 1)  # 무게 m까지 담을 수 있도록
    for _ in range(n): # 짐의 수 만큼
        v, w = map(int, input().split()) # 가치와 무게를 입력
        for j in range(w, m + 1): # 현재 담을 수 있는 짐의 무게부터(짐의 무게보다 작은 가방엔 담지 못한다) ~ 가방 무게까지
            # 점화식을 코드로 표현
            bag[j] = max(bag[j], bag[j-w] + v) # '현재의 짐을 담은 후 가치' VS '현재의 짐을 담기 전 최고의 가치 + 현재 담을 가치'
    print(bag[-1])

if __name__ == '__main__':
    n, m = map(int, input().split())
    Knapsack(n, m)
출력:
36