1. 신경망

신경망은 입력층, 출력층 그리고 은닉층으로 이루어져 있다. 은닉층의 뉴런은 다른 층과 달리 눈에 보이지 않는다.

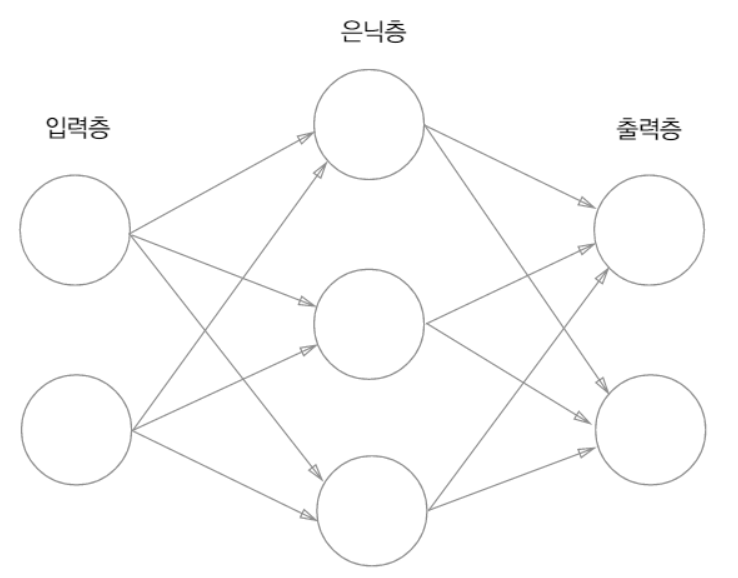
여기까지는 퍼셉트론과 다른 점이 보이지 않는다.

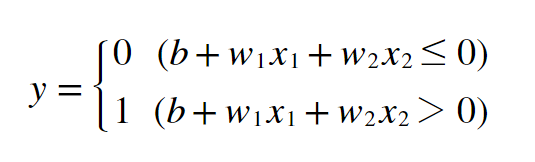
퍼셉트론은 입력갑들과 가중치들을 각각 곱하고, 각 곱들의 합에 편향(b)을 더한 후 다음 뉴런에 전달한다. 그리고 다음 뉴런에서 전달된 값이 0보다 크면 1을 작으면 0을 출력하도록 동작한다.
다시 말해 a = x1w1 + x2w2 + b식에서 a값(신호의 총합)이 출력층 y에 전달이 되어 0을 기점으로 1 아니면 0을 출력하게 된다.
조금 더 간결하게 표현하면, y = h(x1w1 + x2w2 + b)로 나타낼 수 있고 아래와 같은 식으로 나타낼 수도 있다.

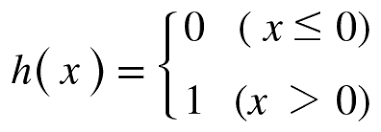
위의 h(a)함수처럼 입력값들을 받아 총합을 출력값으로 변환하는 함수를 일반적으로 활성화 함수라고 한다.
지금까지의 과정을 보면 아래와 같다.

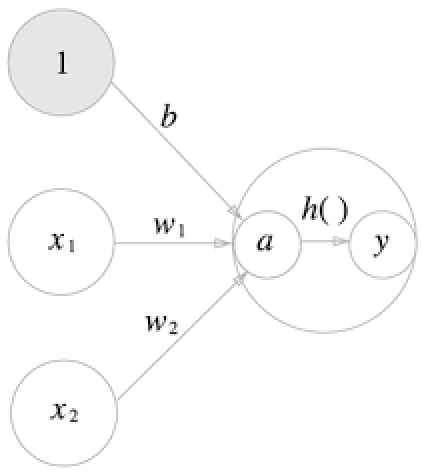
2. 활성화 함수

퍼셉트론은 임계값(b)을 경계로 출력이 바뀌는데, 이런 함수를 계단 함수라고 한다. 앞에서 예로 보았듯이 0을 넘으면 모든 출력값은 1이거나, 0을 이하이면 모든 출력값이 0으로 계단처럼 생겼기 때문에 붙여졌다.
이제 계단 함수에서 다른 함수로 변경하는 것이 신경망의 세계로 나아가는 열쇠가 된다.

계단 함수

간단히 계단 함수를 구현해보자.

# 계단 함수 : True = 1, False = 0을 반환
def step_function(x):
    return np.array(x > 0, dtype=np.int) # x가 0을 넘는다면 True로 1을 반환

X = np.arange(-5.0, 5.0, 0.1) # -5에서 5까지 0.1단위로 값 생성
Y = step_function(X)

plt.figure(figsize=(12, 8))
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)  # y축의 범위 지정
plt.show()

시그모이드 함수

시그모이드 함수를 식으로 나타내면 다음과 같다.

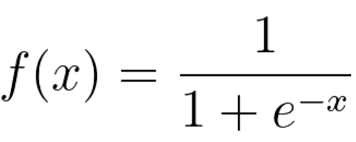
e는 자연상수로 2.7182...의 값을 갖는 실수다. 1에 무한대로 제곱을 해보아도 1이지만, 0에 아주 가까운 0....000001의 값을 1에 더한 후 무한대로 제곱을 하면 2.7182...의 값으로 가까이 소급되어 가는데, 그게 자연상수 e다.

시그모이드 식의 x에 값이 입력되면 출력값은 아무리 커도 1을 넘을 수 없고, 아무리 작아도 0보다 작아질 수 없는 값을 출력으로 가진다.
즉 입력값이 어떻게 입력이 되든 출력은 0과 1사이의 값을 출력하도록 하는 함수가 시그모이드 함수다.

신경망에서는 활성화 함수로 시그모이드 함수를 이용하여 신호를 변환하고, 그 변화된 신호를 다음 뉴런에 전달한다.
그래서 퍼셉트론과 신경망의 차이는 여기까지 보았을 때, 활성화 함수 하나 뿐이다.

시그모이드 함수를 구현해보자.

def sigmoid(x):
   return 1 / (1 + np.exp(-x)) # 자연상수 : np.exp로 표현

X = np.arange(-5.0, 5.0, 0.1)
Y = sigmoid(X)

plt.figure(figsize=(12, 8))
plt.plot(X, Y)
plt.ylim(-0.1, 1.1)
plt.show()

시그모이드와 계단 함수 비교

차이점

계단 함수는 0과 1 둘 중 하나의 값만 출력하는 반면, 시그모이드 함수는 0과 1사이의 실수값을 출력한다.
그래서 퍼셉트론에서는 0과 1사이의 값이 뉴런 사이에서 흘렀다면, 신경망에서는 연속적인 실수가 흐르게 된다.

공통점

비슷한 모양을 지녔듯이, 둘 다 입력이 작을 때에는 출력은 0에 가깝고 입력이 커지면 1에 가까워지는, 혹은 1이 되는 구조다.
즉 아무리 커도 1이며 아무리 작아도 0, 그 사이의 값을 지닌다.
그리고 두 함수 모두 비선형 함수라는 것이다.
이 선형 함수가 아닌 비선형 함수를 사용하는 이유는 신경망의 층을 깊게 쌓을 수 있도록 해주기 때문이다.

비선형 함수

함수란 어떤 입력값이 주어질 때, 그 입력값에 따른 출력값을 내주는 변환기 역할을 한다. 이 함수에 어떤 수를 입력했을 때 입력의 상수배만큼 변하는 함수를 선형 함수라고 한다. 선형 함수는 1개의 직선으로 표현할 수 있다.
비선형 함수는 말 그대로 선형이 '아닌' 함수로써 1개의 직선으로는 그릴 수 없는 함수를 말한다.

선형 함수의 문제는 신경망에서 아무리 층(은닉층)을 쌓더라도, 은닉층이 없는 신경망도 똑같은 기능을 할 수 있다는데 있다.
예로, h(x) = cx를 3층으로 쌓게 되면,
y(x) = h(h(h(x))) -> y(x) = c c c x -> y(x) = c^3 x -> y(x) = ax (a=c^3)으로 3개의 층을 쌓을 필요가 없게 된다.

비선형 함수를 활성화 함수로 쓰는 이유는 층을 쌓기 위해서다.

ReLU 함수

신경망에서 가장 많이 사용하는 활성화 함수로, 입력이 0보다 크다면 그대로 출력을 하고 0보다 작다면 0을 출력하는 함수다.
ReLU 함수를 구현해보자.

def relu(x):
    return np.maximum(0, x)

x = np.arange(-5.0, 5.0, 0.1)
y = relu(x)

plt.figure(figsize=(12, 8))
plt.plot(x, y)
plt.ylim(-1.0, 5.5)
plt.show()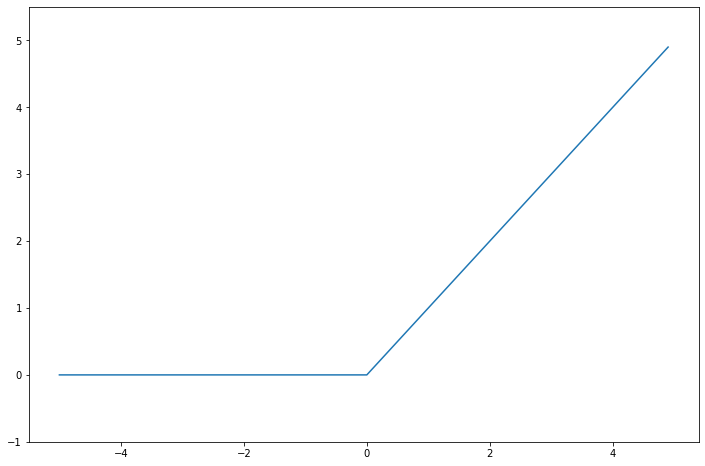

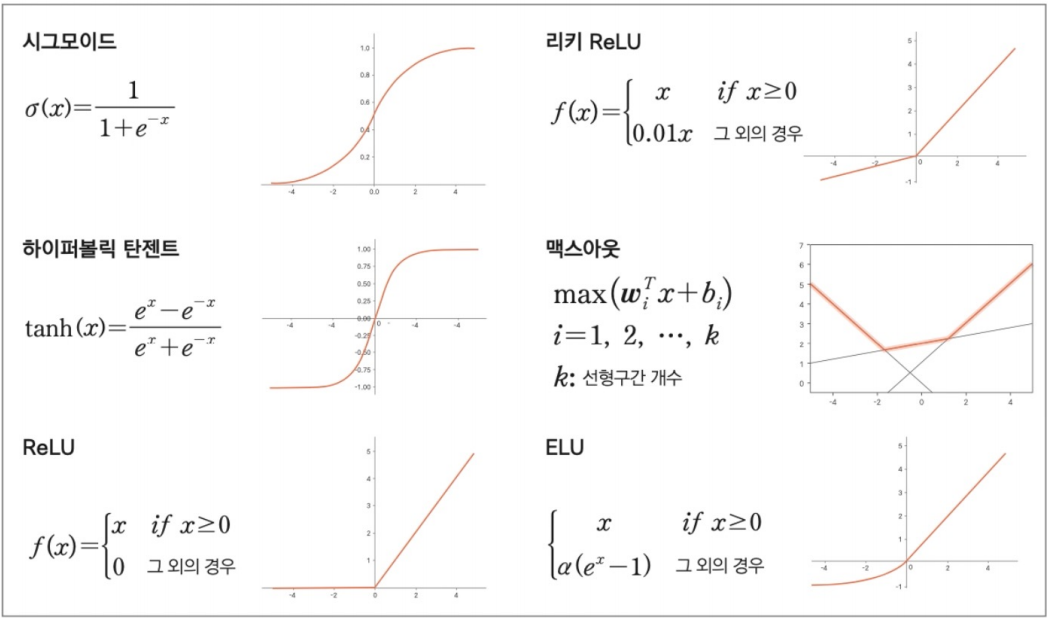
여러 활성 함수들

3. 다차원 배열

다차원 배열은 '숫자의 집합'이다. 숫자가 N차원으로 나열하는 것을 통틀어 다차원 배열이라고 한다.
좀 더 자세한 내용은 '선형대수'를 확인해보자.

행렬의 곱

아래와 같이 행렬의 곱은 '왼쪽' 행렬의 행(가로)과 '오른쪽' 행렬의 열(세로)을 원소별로 곱하고 그 값들을 더해서 계산한다.
np.dot()은 입력이 1차원 배열이면 백터를, 2차원 배열이면 행렬 곱을 계산한다. 행렬의 곱에서 주의할 점은 np.dot(A, B)와 np.dot(B, A)는 다른 값이 될 수 있다는 것이다.

A = np.array([[1, 2], [3, 4]])
A.shape
>
(2, 2)

B = np.array([[5, 6], [7, 8]])
B.shape
>
(2, 2)

np.dot(A, B)
>
array([[19, 22],
       [43, 50]])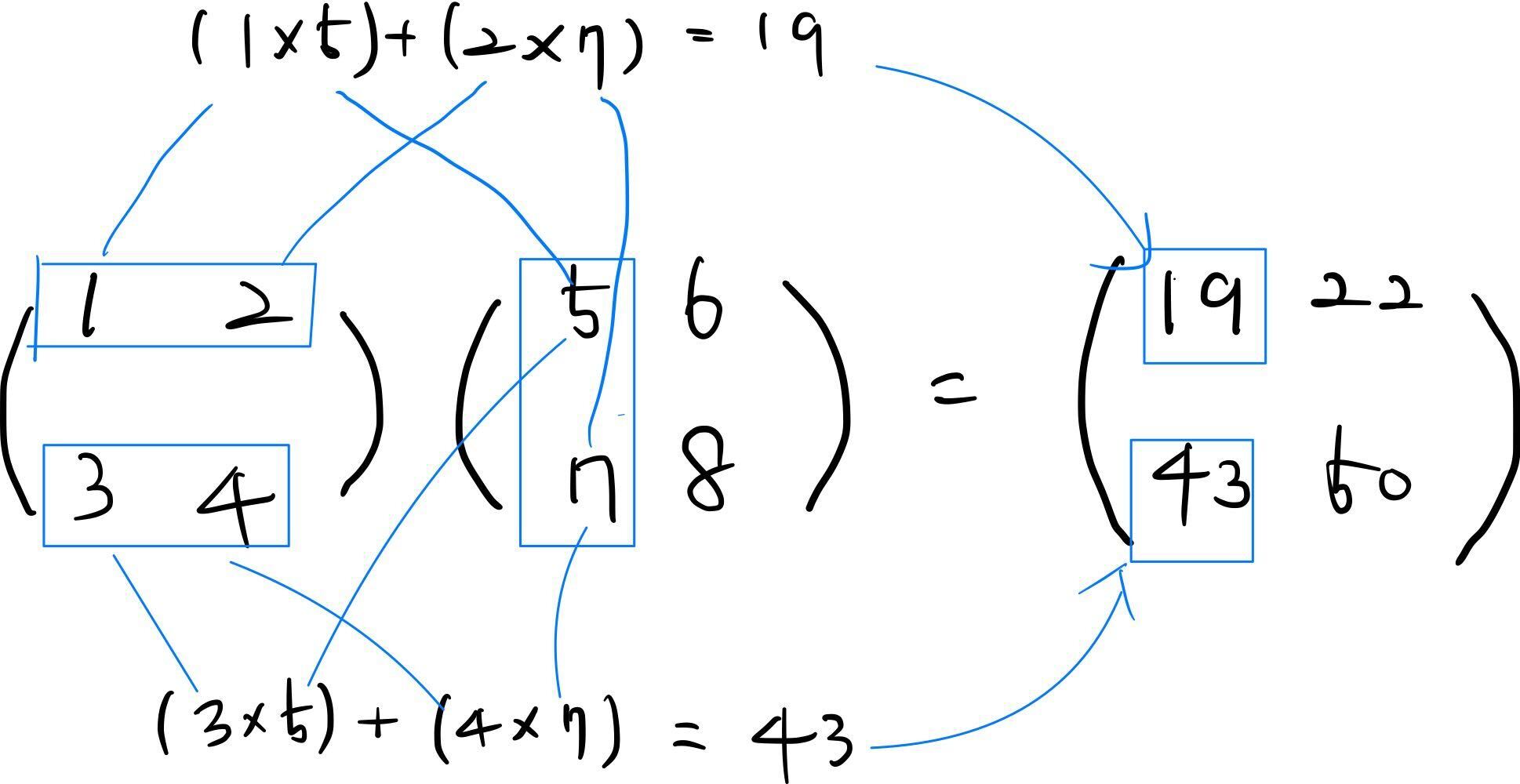

행렬의 곱을 진행할 때 '행렬의 형상'에 주의해야 한다. 미리 말하면 딥러닝에서 학습 시 에러 발생의 대부분은 행렬의 형상이 맞지 않을 때 자주 일어난다.
구체적으로 행렬 A의 1번째 차원의 원소 수와 행렬 B의 0번째 차원의 원소 수가 같아야 한다.

A = np.array([[1, 2, 3], [5, 6, 7]])
A.shape
>
(2, 3)

B = np.array([[1, 2], [3, 4], [5, 6]])
B.shape
>
(3, 2)

np.dot(A, B)
>
array([[22, 28],
       [58, 76]])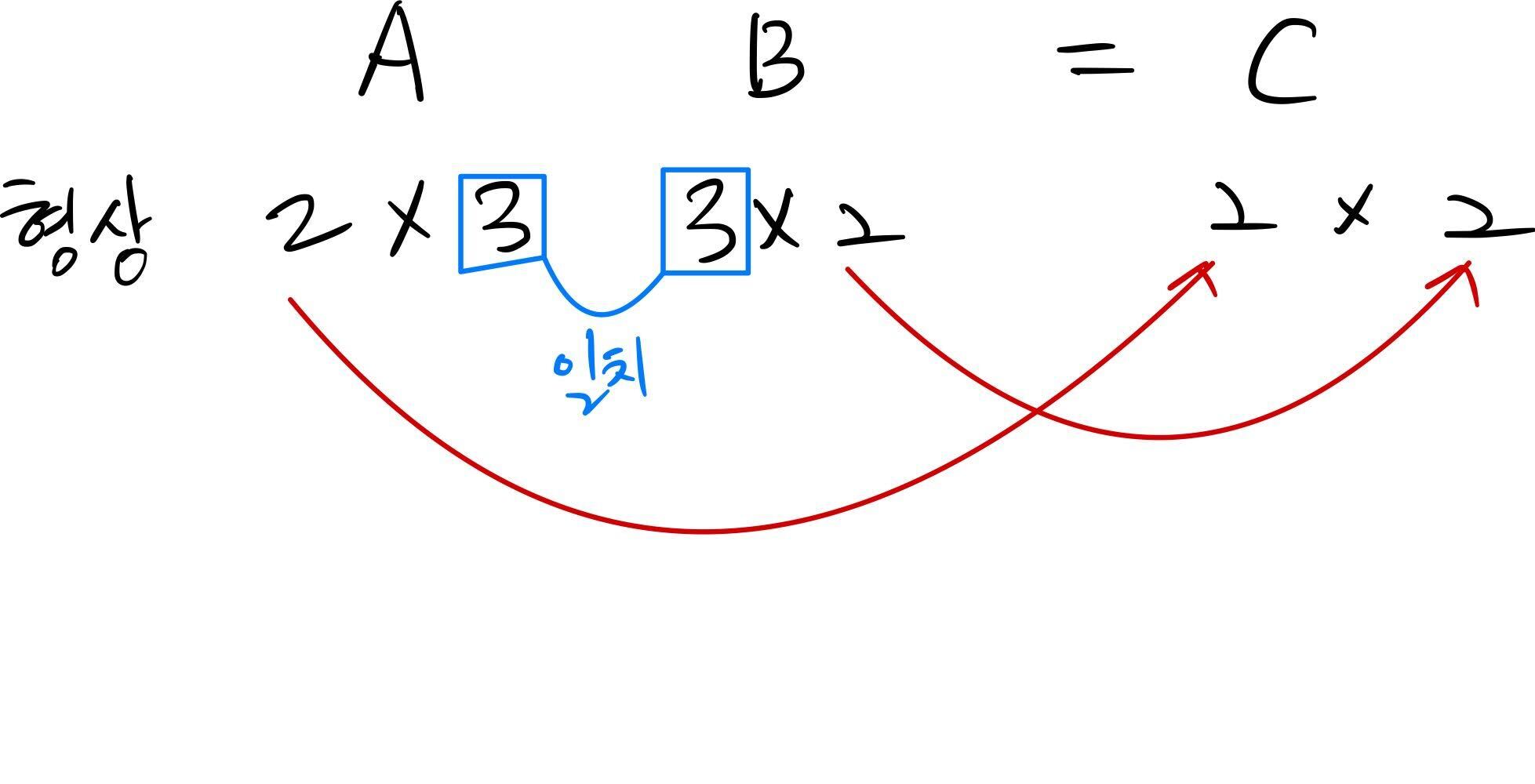

신경망에서의 행렬 곱

신경망의 구현에서도 입력 X에 대한 가중치 W의 대응하는 차원의 원소 수가 같아야 한다.
다차원 배열의 스칼라곱을 구해주는 np.dot()함수는 결과 Y를 단번에 계산할 수 있다.

X = np.array([1, 2])
X.shape
>
(2,)

W = np.array([[1, 3, 5], [2, 4, 6]])
W.shape
>
(2, 3)
print(W)
>
[[1 3 5]
 [2 4 6]]

Y = np.dot(X, W)
print(Y)
>
[ 5 11 17]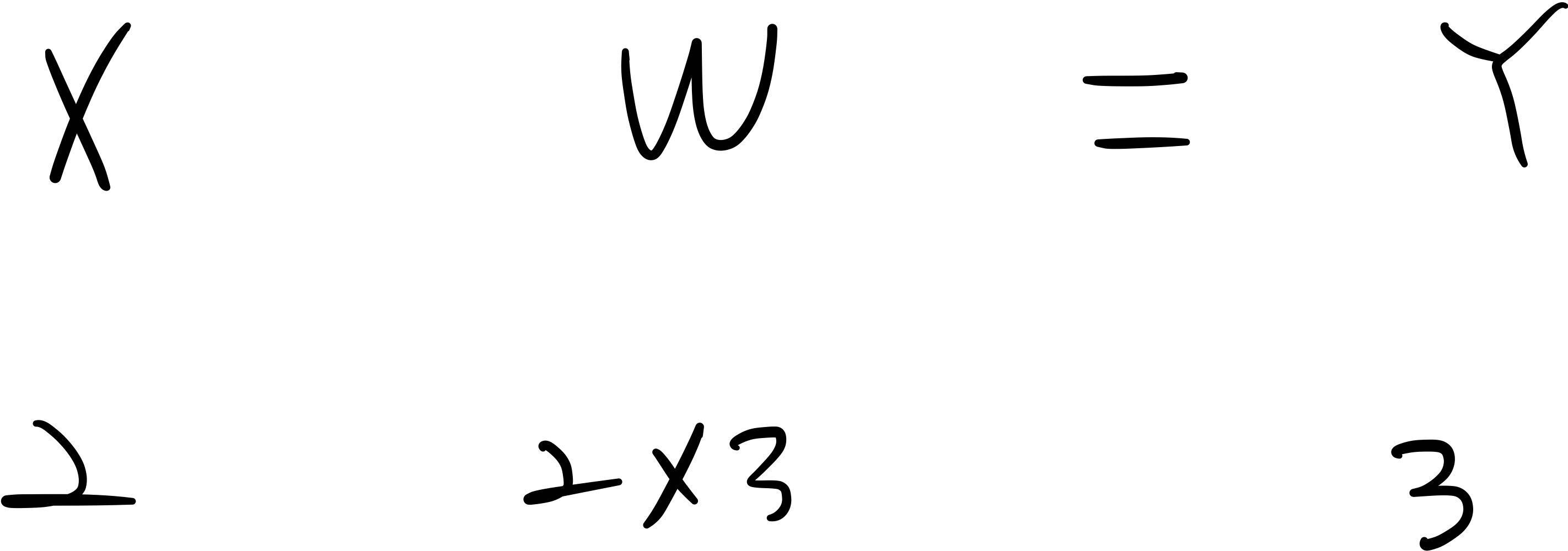

4. 신경망 구현

3층 신경망을 구현해보자.

아래는 3층 신경망의 그림이다.
입력층(0층)은 2개, 첫 번째 은닉층(1층)은 3개, 두 번째 은닉층(2층)은 2개, 출력층(3층)은 2개의 뉴런으로 구성되어 있다.

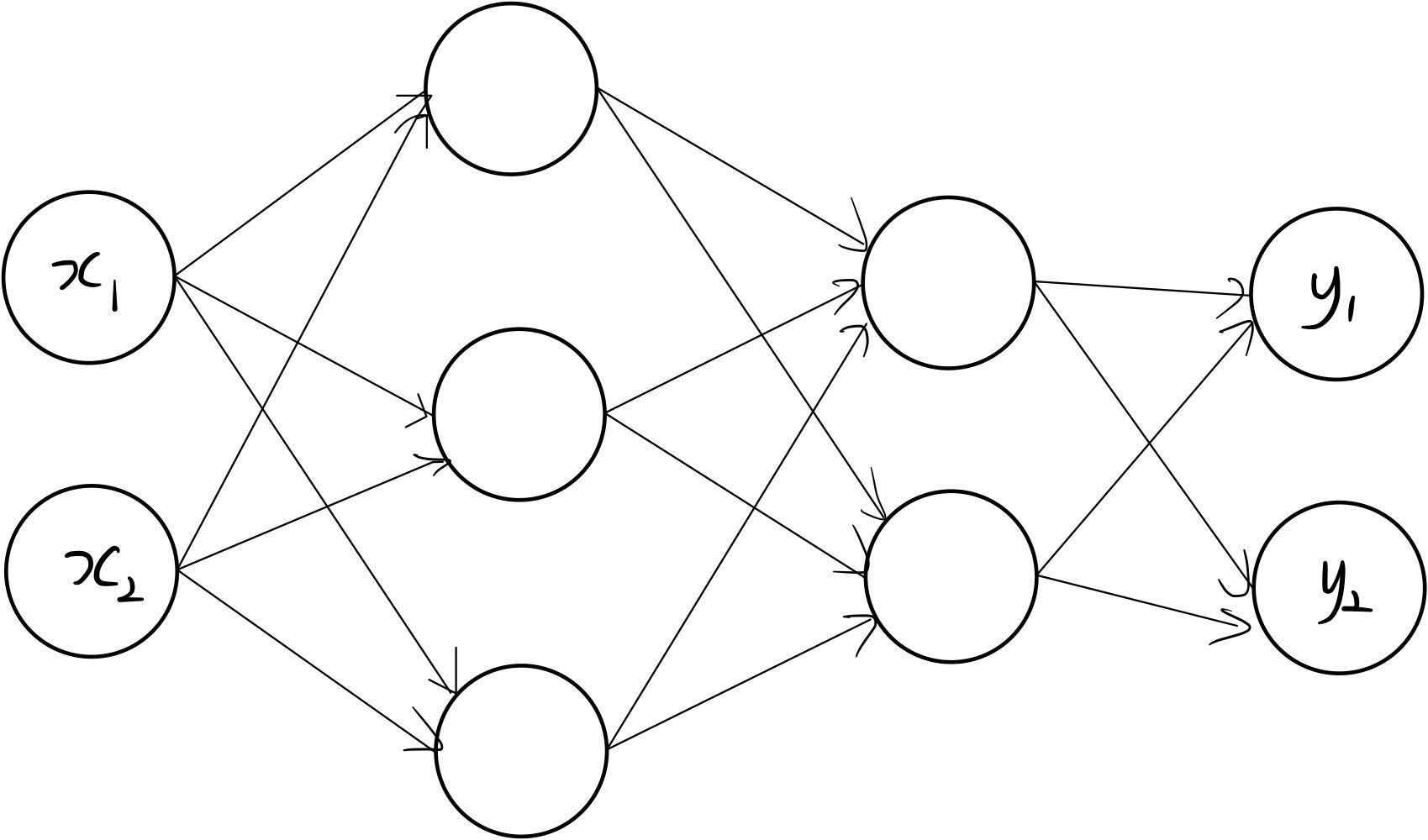
w는 가중치, b는 편향

# 시그모이드 함수
def sigmoid(x):
    return 1 / (1 + np.exp(-x))    

# 소프트맥스 함수
def softmax(x):
    if x.ndim == 2:
        x = x.T
        x = x - np.max(x, axis=0)
        y = np.exp(x) / np.sum(np.exp(x), axis=0)
        return y.T 

    x = x - np.max(x) # 오버플로 대책
    return np.exp(x) / np.sum(np.exp(x))

# 가중치와 편향 정의
def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])

    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])

    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])

    return network

# 신경망 계산
def forward(network, x):
    w1, w2, w3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, w1) + b1 # 1층 : 입력값과 가중치 곱에 편향을 더하고
    z1 = sigmoid(a1) # 활성함수(비선형 함수) 시그모이드 적용
    a2 = np.dot(z1, w2) + b2 # 2층 : 1층값에 2층 가중치 곱에 2층 편향을 더하고
    z2 = sigmoid(a2) # 활성함수(비선형 함수) 시그모이드 적용
    a3 = np.dot(z2, w3) + b3 # 3층 출력층
    y = softmax(a3) # 출력층 함수 : 풀고자 하는 문제의 성질에 맞게 설정

    return y

# 함수 정의
network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)
>
[0.40625907 0.59374093]

5. 출력층

신경망은 분류와 회귀 모두에 이용할 수 있는데, 둘 중 어떤 문제냐에 따라서 출력층에서 사용하는 활성화 함수가 달라진다.

함수

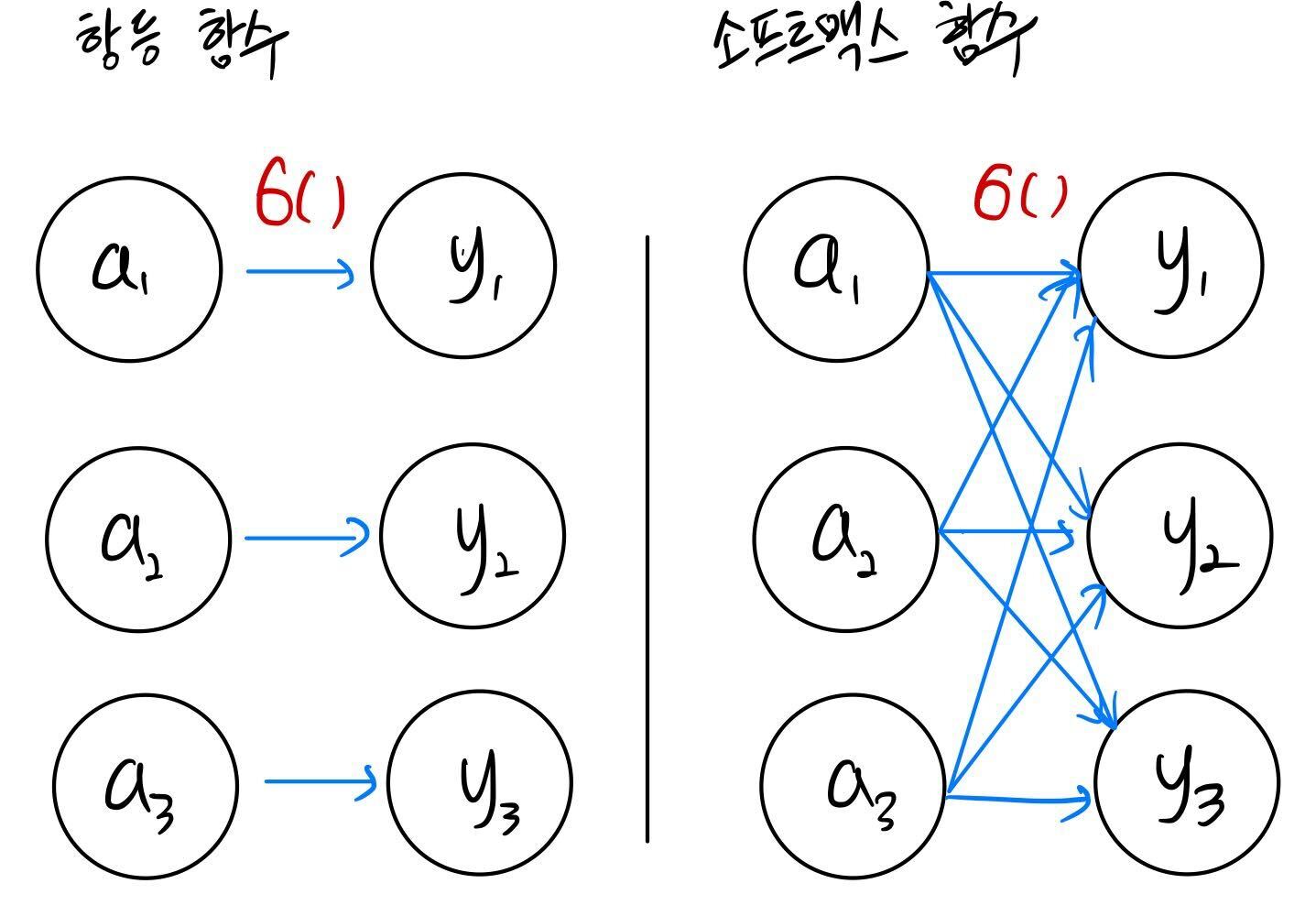
항등 함수

항등 함수(identity function)는 입력을 그대로 출력한다. 입력과 출력이 항상 같다는 뜻의 항등이다. 그래서 출력층에서 항등 함수를 사용하면 입력 신호가 그대로 출력 신호가 된다.

소프트맥스 함수

분류에서 자주 사용되는 것은 소프트맥스 함수(softmax function)이다.
exp(x)는 e^x를 뜻하는 지수 함수이고 e는 자연상수다.
n은 출력층의 뉴런 수를 y값은 그 중에서 k번째 출력을 뜻한다.

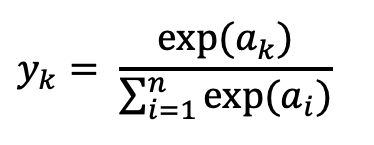
항등 함수는 입력이 그대로 출력값이 되는 것에 반해,
소프트맥스 함수의 출력은 모든 입력 신호로부터 화살표를 받는다.

소프트맥스 함수

주의점

소프트맥스 함수는 지수 함수를 사용하는데 아주 큰 값을 내뱉게 되어 오버플로 문제가 발생된다.
컴퓨터는 4, 8바이트와 같은 크기가 '유한'한 데이터를 다루는데, 수의 범위가 한정되어 있어 매우 큰 값을 표현할 수 없는 문제가 발생한다.(overflow)

a = np.array([1010, 1000, 990])
np.exp(a) / np.sum(np.exp(a))
>
array([nan, nan, nan]) # inf값이 리턴되어 NaN으로

그래서 소프트맥스 계산할 때 분자와 분모에 같은 값을 곱한다. 소프트맥스의 지수 함수를 계산할 때 어떤 정수를 더해도 결과는 바뀌지 않는 것을 이용하여, 오버플로를 막을 목적으로 입력 신호 중 최대값을 이용한다.

# 최대값 찾기
c = np.max(a)
a - c
>
array([  0, -10, -20])

# 오버플로 대책
np.exp(a - c) / np.sum(np.exp(a - c))
>
array([9.99954600e-01, 4.53978686e-05, 2.06106005e-09])

# 소프트맥스 함수
def softmax(a):
    c = np.max(a)
    exp_a = np.exp(a - c)
    sum_exp_a = np.sum(exp_a)
    y = exp_a / sum_exp_a

    return y

특징

softmax() 함수를 사용하면 신경망의 출력은 다음과 같다.

a = np.array([0.3, 2.9, 4.6])
y = softmax(a)
print(y)
>
[0.01134256 0.15271323 0.83594421]

소프트맥스 함수의 특징은 출력값들의 0과 1사이의 값들이며 출력의 총합은 '1'이라는 것이다. 이 성질로 인해 함수의 출력을 '확률'로 해석할 수 있게 된다.

소프트맥스 함수를 적용해도 각 원소의 대소 관계는 변하지 않는다. 이는 지수 함수가 '단조 증가'함수이기 때문이다.(a =< b일 때, f(a) =< f(b))
그래서 a원소들 사이의 대소 관계가 y의 원소들 대소 관계로 그대로 이어진다.

이에,
기계 학습 시 학습과 추론의 과정을 거치는데, 신경망을 학습시킬 때는 출력층의 소프트맥스 함수를 사용하지만, 추론과정에서 분류를 할 때에는 소프트맥스 함수를 생략하는 것이 일반적이다.

출력층 뉴런 수

출력층의 뉴런 수는 문제에 맞게 적절히 정해야 한다.
예로 0부터 9까지의 숫자를 분류할 때에는 뉴런수를 10개로, 개와 고양이를 분류할 때에는 뉴런수를 2개(개, 고양이) 혹은 1개(1은 개, 0은 개가 아닌)로 정할 수 있다.
그 중에서 하나의 값을 내뱉는데, 뉴런수 중에서 가장 큰 값을 정답으로 추론한다.