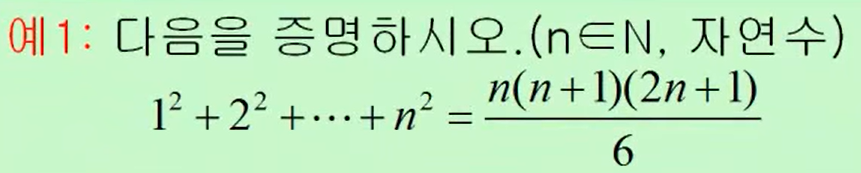1. 추론, 연역법과 귀납법

• 추론(Reasoning, inference)

  : 우리가 이미 "참"으로 알고 있는 명제(들)로부터 새로운 "참"인 명제를 찾아내려고 한다. 이러한 과정을 통해서 새로운 지식을 얻게 된다.

• 올바른 추론의 규칙을 "논리(Logic)"라고 부른다.

• 추론의 방법의 두가지 : 연역법 & 귀납법

• 연역법(Deduction)

  : 일반적인 전제로부터 특정한 결론을 도출하는 논리적인 추론 방법
  

• 귀납법(Induction)

  : 개별적인 사실을 말하는 명제들로부터 일반적인 결론을 도출하는 방법
  

• 귀납법의 한계 : 현실적으로 집합의 모든 원소에 대해서 참인 것을 밝힐 수 없다는 점. 따라서 도출된 결론은 기껏해야 확률적인 결론일 수 밖에 없다.

• 수학적 귀납법(Mathematical Induction)

  : 모든 자연수가 어떤 주어진 성질을 만족시킨다는 명제를 증명하는 방법의 하나
  : 집합의 모든 원소에 대해서 명제가 성립하는 것을 보여준다. 따라서 모든 경우에 명제가 성립하는 것을 증명할 수 있다.
  

• 예시 문제
  
  

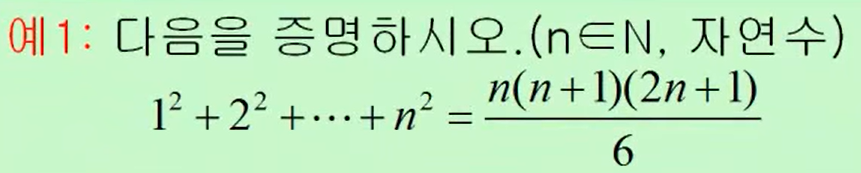
2. 부울대수와 논리회로 설계

부울 대수(Boolean algebra)

• 보수 : '로 표시
  : 원소 0에 대하여 0' = 1, 원소 1에 대하여 1' = 0
• 합 : +(또는 OR)로 표시
  : 1+1=1, 1+0=1, 0+1=1, 0+0=0
• 곱 : •(또는 AND)로 표시 (•는 생략하여 표기하기도 한다.)
  : 1•1=1, 1•0=0, 0•1=0, 0•0=0
• 연산 우선순서 : 보수 >> 곱 >> 합
• 부울 변수(Boolean variable)
  : 집합 S={0,1}의 원소 값만을 갖는 변수
• 부울 함수(Boolean function)
  : 0 또는 1의 입력값들에 대하여 0 또는 1의 출력값을 갖는 함수
• 부울 식(Boolean expression)
  : X1,X2,...,Xn = 부울대수
  (1) 0,1,X1,X2,...,Xn은 부울식이다.
  (2) E1, E2가 부울식이면, E1, (E1•E2), (E1+E2)도 부울식이다.
• 항등(Equivalence)
  : 동일한 변수값에 대해서 진리표의 결과값이 동일하면 두 부울 함수는 동등하다.
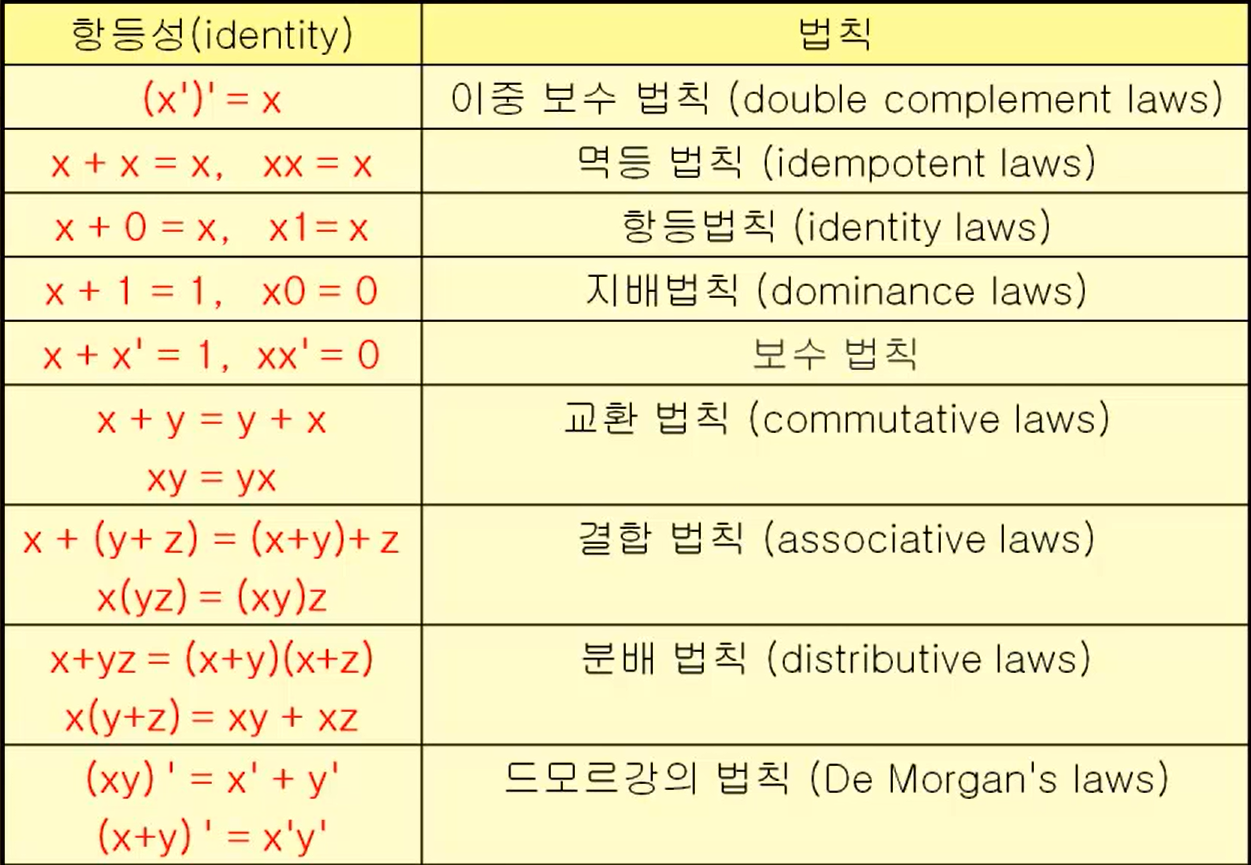
• 부울대수의 법칙
  
  
  
• 최소항
  : 최소항은 주어진 부울 함수에서 출력이 참인 최소한의 조건을 나타냅니다. 이는 입력 변수들 중 어떤 조합이 참일 때 함수의 출력이 참이 되는지를 나타냅니다.

• 게이트와 부울 연산
  : 전자 장치의 입력과 출력은 0 또는 1이기 때문에 전자 회로를 설계하는데 부울 대수를 사용할 수 있다.
• 게이트(gate): 회로의 기본 요소
  
  

  ---

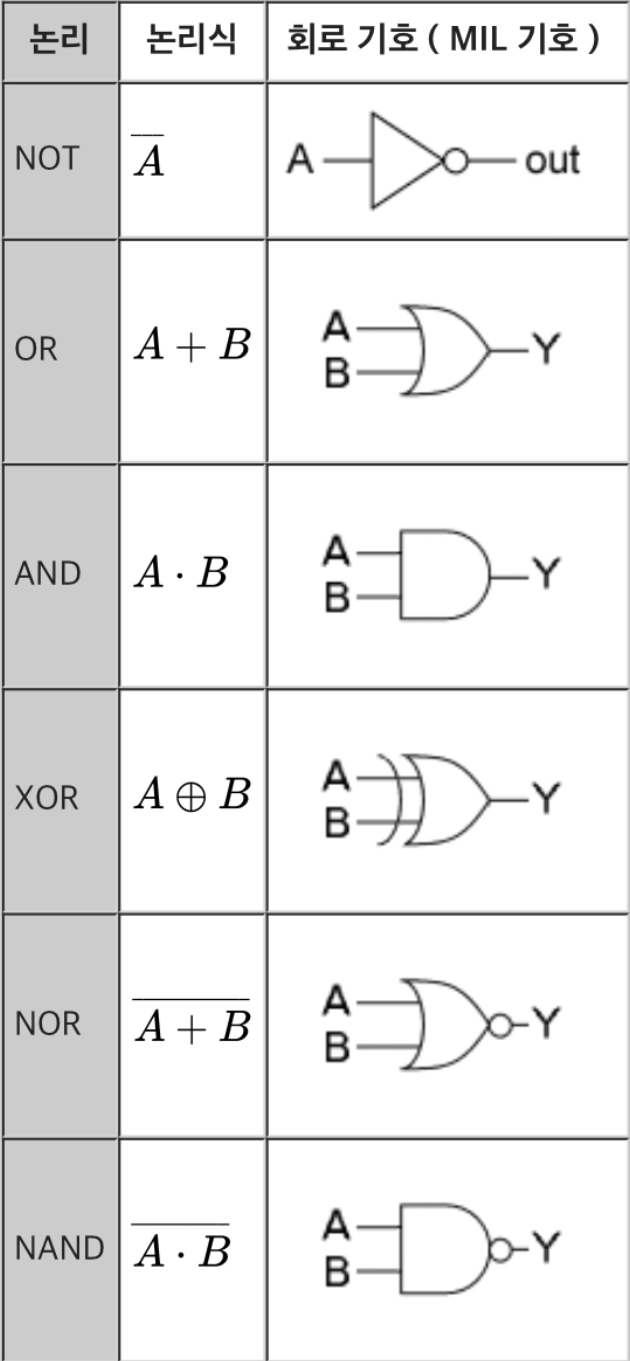
• 논리 회로 설계
  : 문제 -> 입력과 출력 정의 부울 함수 -> 부울식(논리식) -> 논리 회로
• 부울식의 항등관계(Identity)
  : 부울 대수에서 두 부울식이 동일한 논리적 의미를 가지는 관계를 말한다.
  즉, 두 부울식이 모든 입력에 대해 항상 동일한 출력 값을 가질 때, 그 두 부울식은 항등관계에 있다고 말할 수 있다.

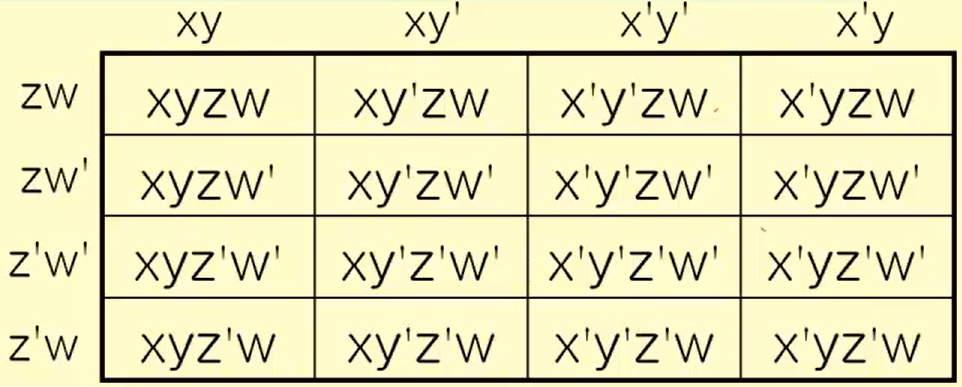
• 카르노맵(Karnaugh Map)
  : 부울 대수에서 부울 함수를 시각적으로 표현하고 분석하는 데 사용되는 방법.
  ex) 1. x'y'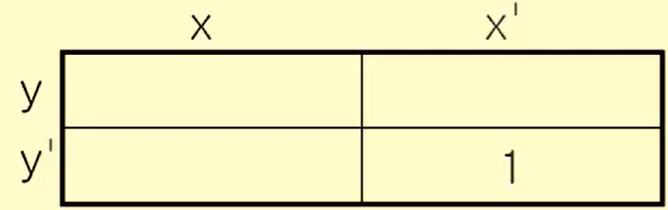
  ex) 2. xy + xy' + x'y + x'y'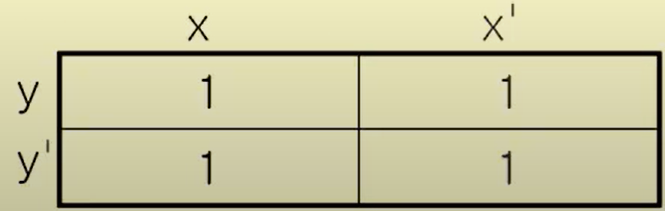
  
  
• 4개의 변수