[이산수학] 이산수학/명제기초

SELOG·2023년 6월 30일

이산수학

목록 보기

1/2

이산수학(Discrete Mathematics)
- 불연속적 수학 ( =컴퓨터를 위한 수학 )
- 참과 거짓으로 살펴보는 컴퓨터 수학
이산수학을 왜 배워야 할까?
- 이산수학이란 불연속적인 숫자를 다루는 수학이다.
- 컴퓨터에서는 내부적으로 0과 1을 다루는 데 그러한 불연속적인 데이터의 흐름을 다루기에 적합한 수학적 사고를 배양하는데 필수적 관문
- 자료구조, 알고리즘 등의 베이스가 되어 전체적인 컴퓨터 사고력을 길러줄 것
- 추후에 배우는 수학적 귀납법 등의 다양한 기초 개념이 알고리즘에 반복적으로 출현하기 때문에 컴퓨터 과학의 베이스 학문이라 할 수 있다.

명제
진실 or 거짓
- 참(True)이나 거짓(False)으로 진리를 구분할 수 있는 문장
- 명제는 0 또는 1만을 가지는 컴퓨터 메모리처럼 항상 참과 거짓 둘 중 하나의 값만을 가진다.
- 여러 개의 명제를 조합할 수 있다.
연산자로 명제 다루기
- 연산자는 명제를 연산하기 위한 도구이다.
- 이산수학의 기본 연산자로는 6가지가 있다.
- 합성명제(Compound Proposition) : 여러 개의 명제를 합친것.
- 조건명제(Conditional Proposition) : 원인이 되는 명제와 결과가 되는 명제가 존재하는 명제.
1. 부정, Not(￢ )
- 명제의 진리값을 뒤집어줌
- p⇒ 참
- ￢p ⇒ 거짓
2. 논리곱, And( ^ )
- p ^ q 일때 p,q모두 참일 경우에만 p ^ q⇒ 참 이다 나머지는 거짓
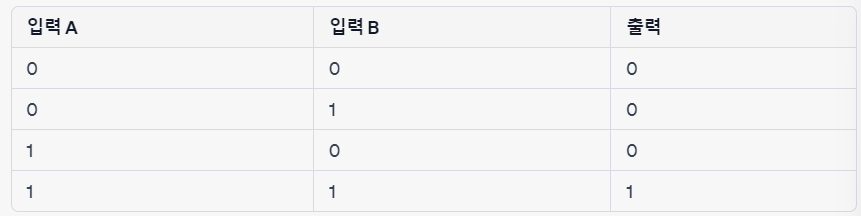
3. 논리합, Or( v )
- p v q 일때 p,q모두 거짓일 경우에만 p v q⇒ 거짓 이다 나머지는 참
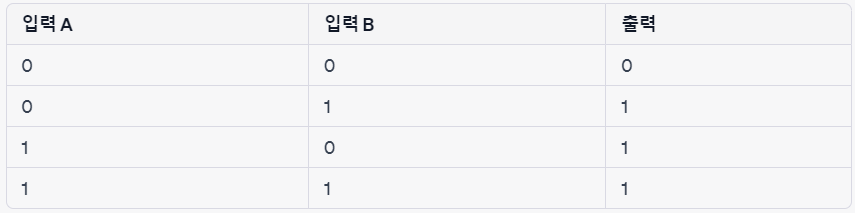
4. 배타적논리합, Exclusive or( ⊕ )
- p, q가 다르면 참
- p, q가 같으면 거짓
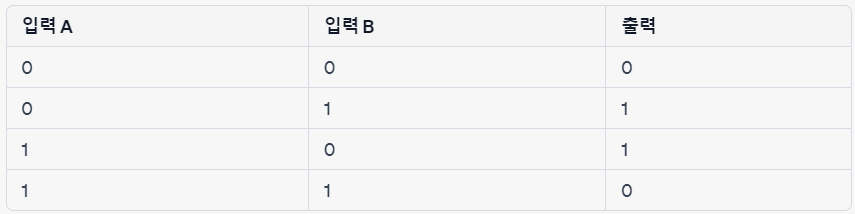
5. 조건명제, Implication (→)
- p → q : p일때 q이다
- 조건 → 결과
- 참 → 거짓 ⇒ 거짓 나머지 경우는 참
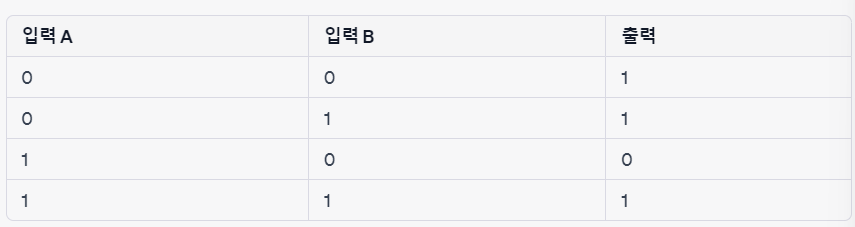
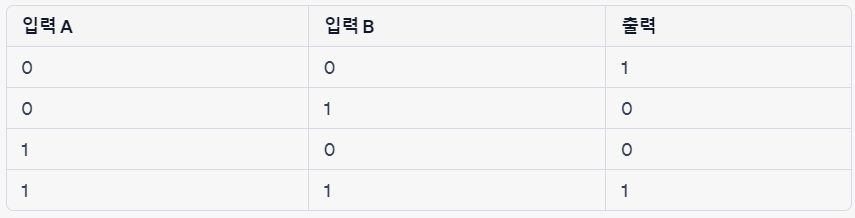
6. 쌍방 조건명제, Biconditional (↔)
- p, q가 같으면 참
- p, q가 다르면 거짓
- 배타적논리합(⊕)의 반대

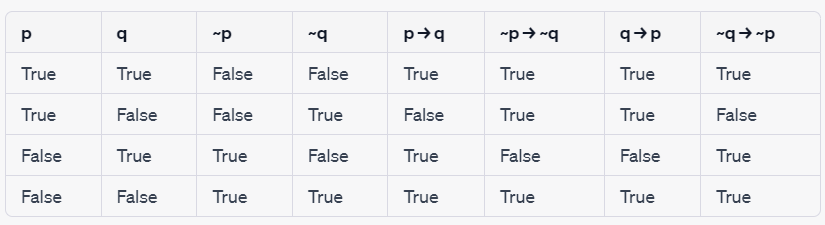
진리표
- 각 명제 사이의 관계식의 진릿값을 보여주는 표
- 아무리 복잡한 합성 명제라도 진리표로 풀어낼 수 있다.
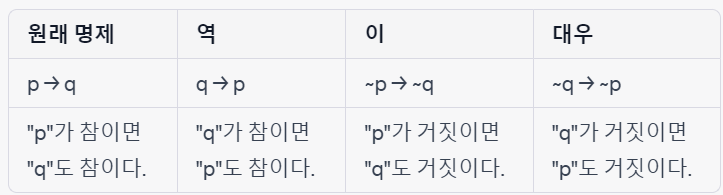
역,이,대우
- 역, 이, 대우는 조건명제에서 사용한다.
- 역, 이, 대우는 하나의 명제를 변형해 표현한다.
- 증명하기 어려운 명제는 대우를 이용해 증명할 수 있다. ( 원래 명제와 대우가 논리적으로 동치이기 때문이다 )

동치
- 두 개의 명제가 논리적으로 완전히 동일한 것을 말한다.
- 동치 관계에 있는 명제들은 서로 동일한 진리값을 가지며, 하나의 명제를 다른 명제로 대체하여 사용할 수 있다.
  즉, 동치인 명제들은 서로 대체 가능하다는 것을 의미
- 같은 의미를 가진 더 쉬운 명제를 발견하는 데 사용한다.
논리적 동치법칙 多

1. 이중 부정 법칙 (Double Negation):

~~p ≡ p

2. 드모르간의 법칙 (De Morgan's Laws):

~(p ∧ q) ≡ ~p ∨ ~q
~(p ∨ q) ≡ ~p ∧ ~q

3. 교환 법칙 (Commutative):

p ∧ q ≡ q ∧ p
p ∨ q ≡ q ∨ p

4. 결합 법칙 (Associative):

(p ∧ q) ∧ r ≡ p ∧ (q ∧ r)
(p ∨ q) ∨ r ≡ p ∨ (q ∨ r)

5. 분배 법칙 (Distributive):

p ∧ (q ∨ r) ≡ (p ∧ q) ∨ (p ∧ r)
p ∨ (q ∧ r) ≡ (p ∨ q) ∧ (p ∨ r)

6. 전이 법칙 (Transitive):

[(p → q) ∧ (q → r)] → (p → r)

7. 쌍중 감축 법칙 (Biconditional Simplification):

(p ↔ q) ≡ (p → q) ∧ (q → p)

끗

금융 IT 전문가가 될거야