
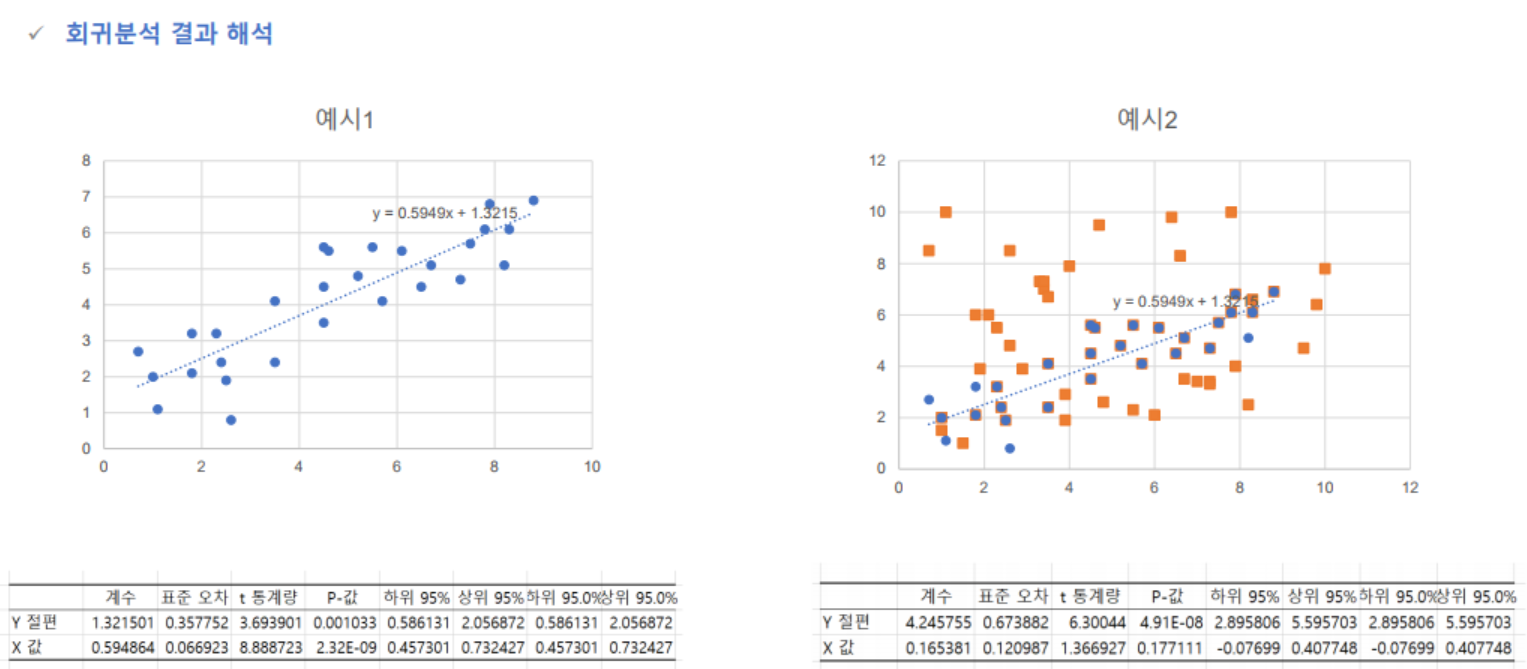
✔️ 통계 심화 3~6
회귀분석
- 회귀 분석(regression analysis):
- 변수들간의 함수적 관계를 선형으로 추론하는 통계적 분석 방법으로 독립변수를 통해 종속변수를 예측하는 방법 - 비선형인 함수적 관계일 경우 비선형회귀 (nonlinear regression)를 사용
- ex:) 마케팅 비용에 따른 매출액을 예측
- 종속 변수(dependent variable)
- 다른 변수의 영향을 받는 변수로 반응변수라 표현 하기도 하며, 예측을 하고자 하는 변수 - ex:) 매출액, 수율, 불량율 등
- 독립 변수(independent variable)
- 종속변수에 영향을 주는 변수로 설명변수라 표현하기도 하며, 예측 하는 값을 설명해주는 변수
- 회귀 모델링 분류
- X변수의 수, X변수와 Y변수의 선형성 여부에 따라 구분
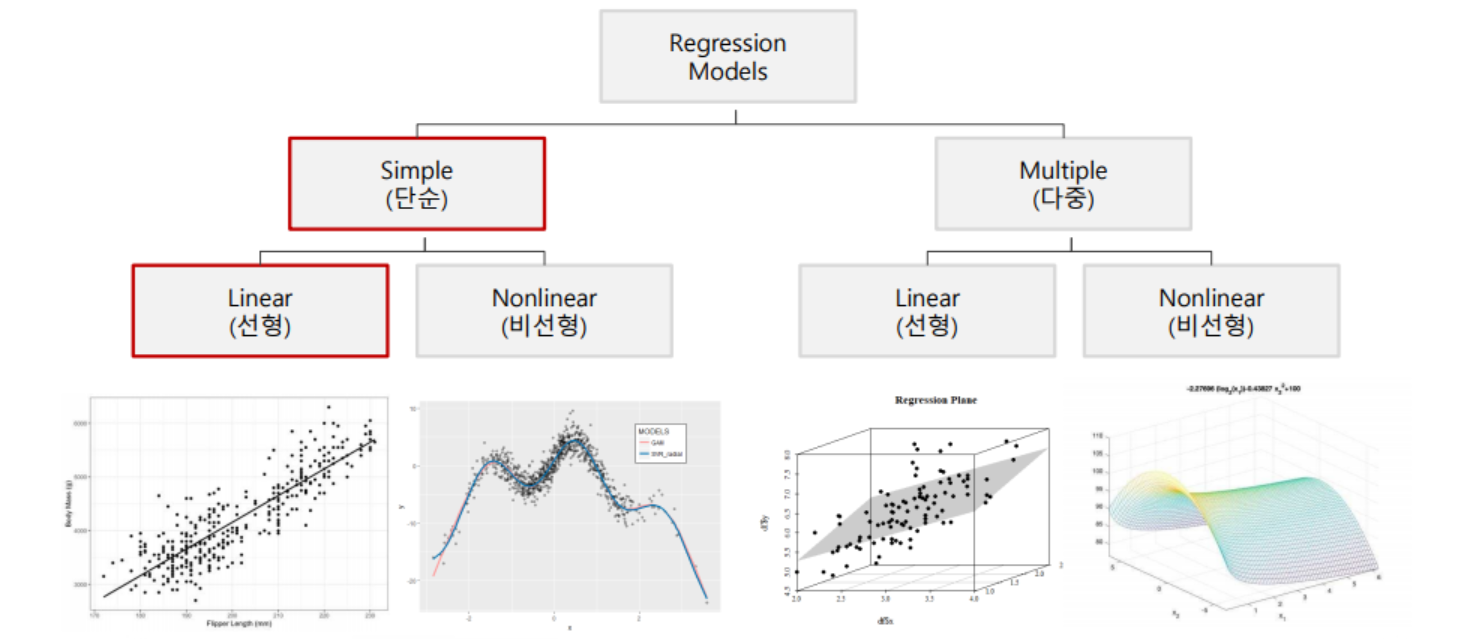
- X변수의 수, X변수와 Y변수의 선형성 여부에 따라 구분
1. 단순 회귀분석
- 하나의 독립변수로 종속변수를 예측하는 회귀 모형을 만드는 방법을 단순 회귀분석이라고 함

- 회귀선으로부터 각 관측치의 오차를 최소로하는 선을 찾는 것이 핵심
- 오차를 최소로 하여 β₀, β₁을 추정하는 방법을 최소제곱법(method of least squares)이라 함
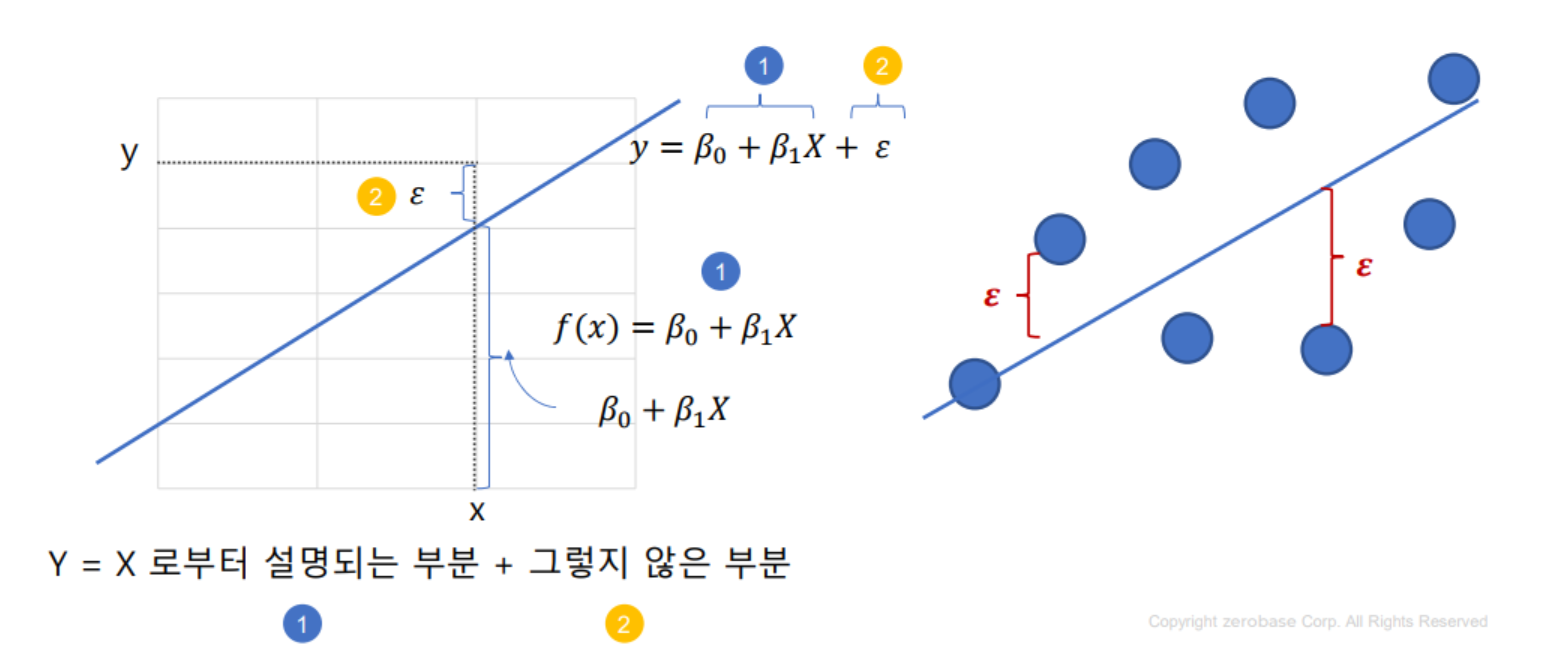
- 최소 제곱법
- 회귀 모형의 모수 â, â 을 추정하는 방법중 하나를 최소 제곱법이라고 하며, 회귀 모형의 모수를 회귀 계수라고 함
- 최소 제곱법을 통해 구한 추정량을 최소제곱추정량(LSE)라고 하며, 최소제곱법을 통해 회귀모형의 모수를 추정하는 것을 OLS(Ordinary Least Square) 라고 함
- 회귀 모형의 오차에 대하여 기본 가정이 있음
1) 정규성 가정: 오차항은 평균이 0인 정규 분포를 따름
2) 등분산성 가정: 오차항의 분산은 모든 관측값 rX에 상관없이 일정함
3) 독립성 가정: 모든 오차항은 서로 독립임
- 분산분석표
- 추정된 회귀식에 대한 유의성 여부는 분산분석을 통해서 회귀식의 유의성을 판단 할 수 있음
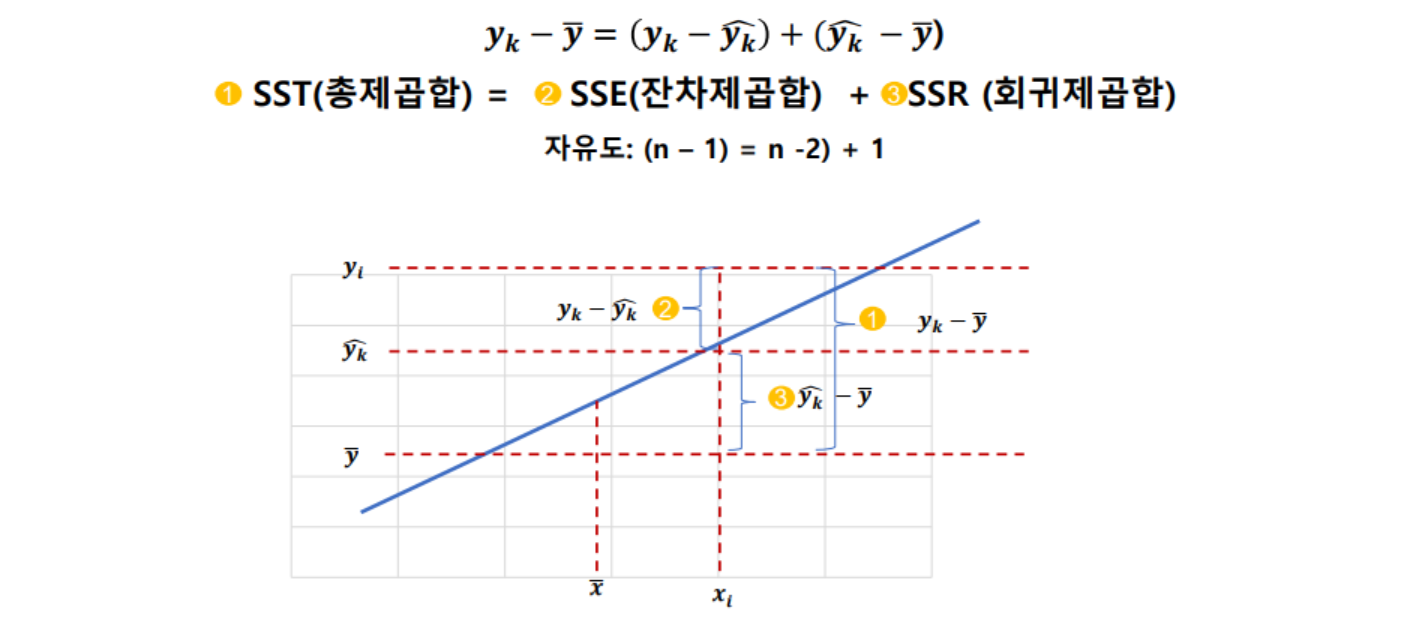
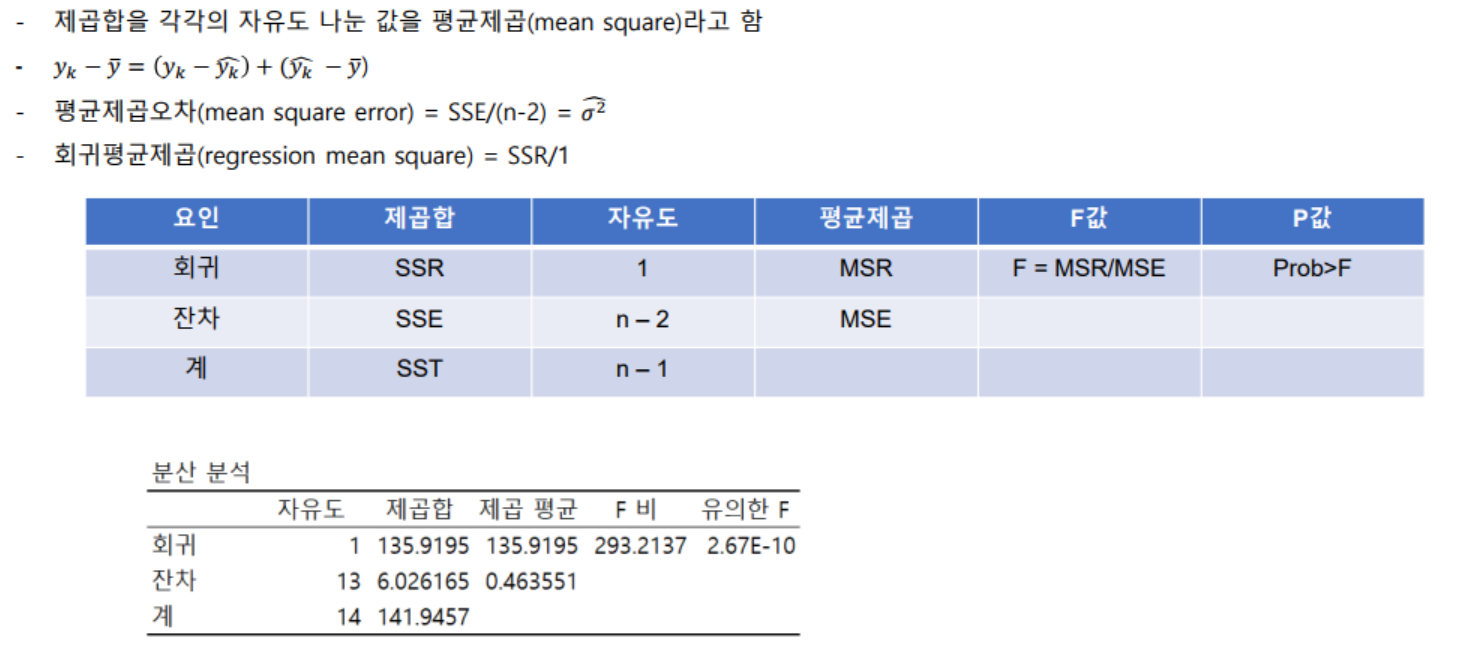


- 추정된 회귀식에 대한 유의성 여부는 분산분석을 통해서 회귀식의 유의성을 판단 할 수 있음
- 결정 계수 (Coefficient of determination: R²)
- 추정된 회귀식이 얼마나 전체 데이터에 대해서 적합한지(설명력이 있는지)를 수치로 제공하는 값

- 0과 1사이에 값으로 1에 가까울수록 추정된 모형이 설명력이 높다고 할 수 있음
- 0이라는 것은 추정된 모형이 설명력이 전혀 없다고 할 수 있음

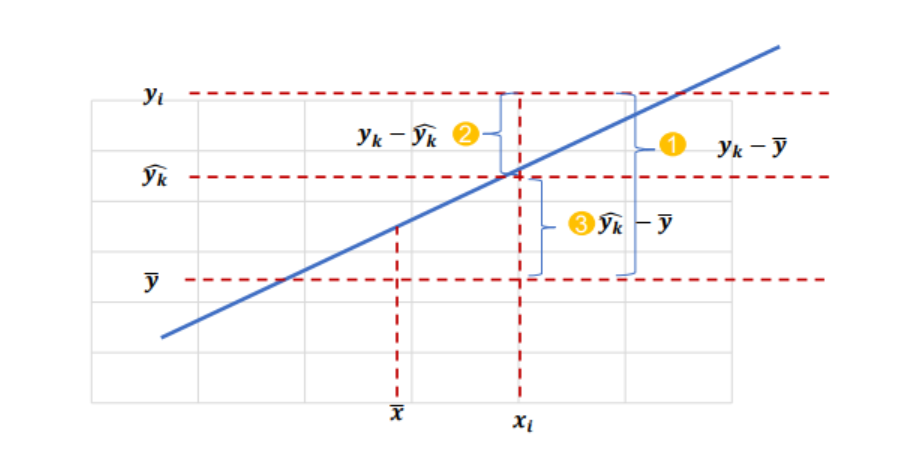
- 추정된 회귀식이 얼마나 전체 데이터에 대해서 적합한지(설명력이 있는지)를 수치로 제공하는 값
- 수정 결정 계수 (Adjust R²)
- R²은 유의하지 않은 변수가 추가되어도 항상 증가됨(다중회귀)
- Adjust R²은 특정 계수를 곱해 줌으로서 R²가 항상 증가하지 않도록 함
- 보통 모형 간의 성능을 비교할 때 사용함
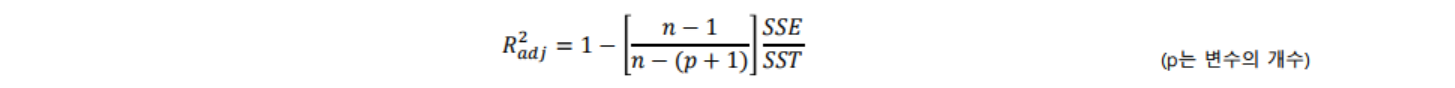
- 잔차 분석
- 선형성을 벗어나는 경우
- 종속변수와 독립변수가 선형 관계가 아님
- 등분산성이 벗어난 경우
- 일반적인 회귀모형 사용 불가능 - 등분산성 가정 위배
- 독립성에 벗어나는 경우
- 시계열 데이터 또는 관측 순서에 영향을 받는 데이터 에서는 독립성을 담보 할 수 없음(Durbin-Watson test 실행)
- 정규성을 벗어 나는 경우
- Normal Q-Q plot으로도 확인
- 잔차가 -2 ~ +2 사이에 분포 해야 함
- 벗어나는 자료가 많으면 독립성 가정 위배
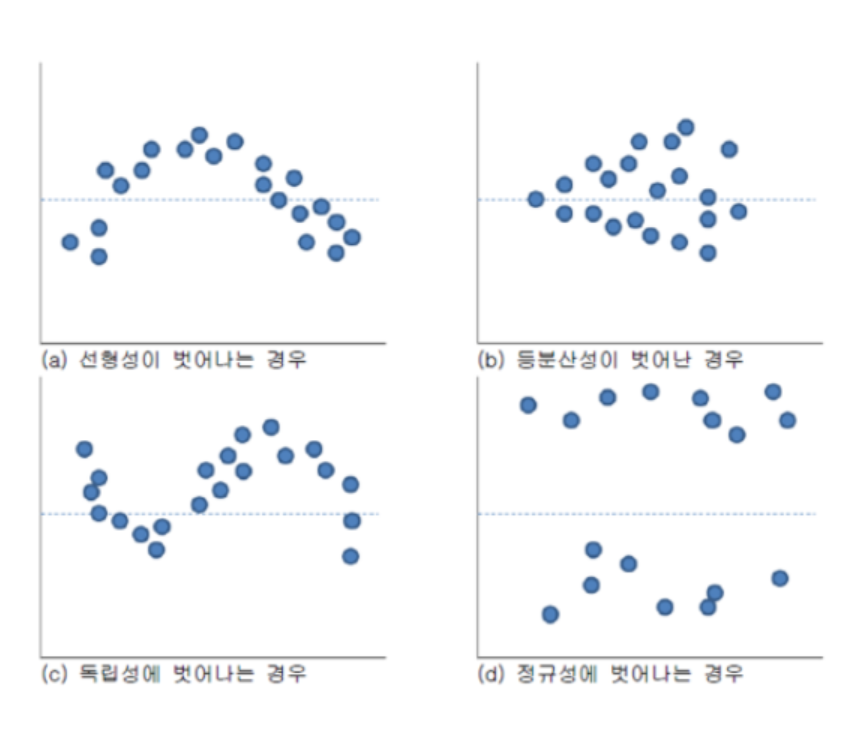
- 선형성을 벗어나는 경우
2. 다중 회귀분석
- 다중 회귀분석(multiple regression analysis)
- 2개 이상의 독립변수로 종속 변수를 예측하는 회귀 모형을 만드는 방법을 다중 회귀분석이라고 함

- 2개 이상의 독립변수로 종속 변수를 예측하는 회귀 모형을 만드는 방법을 다중 회귀분석이라고 함
- 로지스틱 회귀분석(Logistic regression analysis)
- 반응 변수가 범주형(이진수)인 경우 사용하는 모형
- 다항 회귀분석(polynomial regression)
- 독립 변수가 k개이고 반응 변수와 독립변수가 1차 함수 이상인 회귀 분석
- 변수선택법
- 전진선택법(forward selection) : 독립변수를 1개부터 시작하여 가장 유의한 변수들부터 하나씩 추가하면서 모형의 유의성을 판단하는 방법
- 후진 제거법(backward selection) : 모든 독립변수를 넣고 모형을 생성한 후, 하나씩 제거하면서 판단하는 방법
- 단계접 방법(stepwise selection) : 위의 두가지 방법을 모두 사용하여 변수를 넣고 빼면서 판단하는 방법
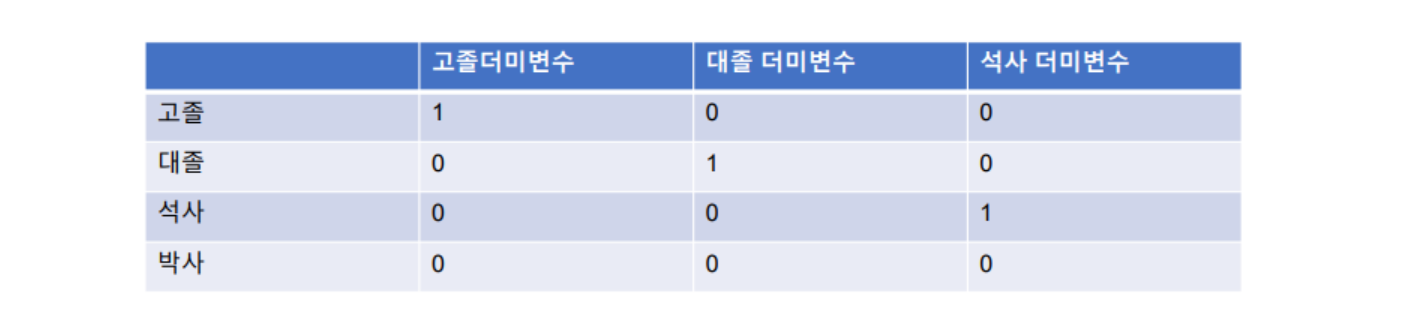
- 더미 변수(dummy variable)
- 값이 ‘0‘ 또는 ‘1’로 이루어진 변수
- 지금까지 회귀분석에서는 연속형 변수를 사용하는 예를 들었지만, 범주형 변수를 사용하기 위해서는 더미변수가 필요함
- 예를 들어 사는 지역을 ‘1’, ‘2’, ‘3’으로 사용하면 연속형 변수여서 정확한 변수로 사용할 수 없음
- 범주형 변수를 0과 1의 조합으로 표현 할 수 있도록 더미 변수를 생성함
- 예시) 최종 학력: 고졸, 대졸, 석사, 박사 4가지로 표현 한다면 필요한 더미의 개수는 4-1 = 3개임
- 다중공선성(Multicollinearity)
- 상관관계가 높은 독립변수들이 동시에 사용될 때 문제가 발생
- 결정계수 R²값은 높아 회귀식의 설명력은 높지만 독립변수의 P-value 커서 개별 인자들이 유의하지 않는 경우 의심할수 있음
- 일반적으로 분상팽창요인 (Variance Inflation Factor: VIF)이 10 이상이면 다중공선성이 존재함
- 해결 방안
1) 다중공선성이 존재 하지만 유의한 변수인 경우 목적에 따라서 사용할 수 있음
2) 변수 제거
3) 주성분분석으로 변수를 재조합
분산분석
- 분산분석(analysis of variance)
- 셋 이상의 모집단의 평균 차이를 검정
- t-test
- 두개의 모집단의 평균 차이를 검정
- 만약 아래의 평균 차이 검정을 t-test로 한다면
1) (모집단1 – 모집단2, 모집단1 – 모집단3, 모집단2 – 모집단3) 3번의 검증을 해야함
2) 오차가 커짐(α = 0.05인 경우 3번의 비교로 α=1-(1-0.05)³ = 0.143)
분산분석의 이해
- 실험계획법(experimental design): 모집단의 특성에 대하여 추론하기 위해 특별한 목적성을 가지고 데이터를 수집하기 위한 실험 설계를 실험계획법이라고 함
- 반응변수: 관심의 대상이 되는 변수
- 요인/인자(Factor): 실험 환경 또는 조건을 구분하는 변수로 실험에 영향을 주는 변수
- 인자수준: 인자가 취하는 개별 값(처리:treatment)
- 왜 분산분석일까?
- 모집단의 평균들을 비교하기 위하여 특성값의 분산 또는 변동을 분석하는 방법
- 실험을 통해 얻은 편차의 제곱합을 통해 평균의 차이를 검정
- 왜 분산분석일까?
- 분산분석의 기본 가정
1) 각 모집단은 정규 분포를 따른다
2) 각 모집단은 동일한 분산을 갖는다
3) 각 표본은 독립적으로 추출되었다 - 분산분석의 가설과 실험의 가정
- 가설
- H₀ : 각 집단의 평균은 동일하다 vs H₁ : 각 집단의 평균에 차이가 있다
- 실험의 가정
- 반복의 원리: 실험을 반복해서 실행해야 함
- 랜덤화의 원리: 각 실험의 순서를 무작위로 해야함
- 블록화의 원리: 제어해야 할 변수가 있다면 인자에 영향을 받지 않도록 조건을 묶어서 실험해야 함
- 가설
- 분산 분석 종류
- 일원 분산분석 : 한가지 요인을 기준으로 집단간의 차이를 조사하는 것
- 이원 분산분석 : 두 가지 요인을 기준으로 집단 간의 차이를 조사하는 것
- 다원 분산분석 : 세 가지 이상의 요인을 기준으로 집단 간의 차이를 조사하는 것
1. One-way ANOVA
- One-way ANOVA
- 한 개의 반응 변수와 한 개의 독립 인자
- 반응 변수 : 연속형 변수만 가능
- 독립 인자(변수) : 이산형 또는 범주형 변수만 가능


2. Two-way ANOVA
- two-way ANOVA
- 한 개의 반응 변수와 두 개의 독립 인자로 분석하는 방법
- Ex) 만족도에 영향을 주는 인자가 편의점 브랜드와 상권이라고 할 때, 편의점 브랜드별로 상권을 변경하면서 만족도가 다른지 측정하고 분석하는 방법
- 독립인자는 one-way와 마찬가지로 이산형 또는 범주형 변수만 가능


시계열 분석
- 시계열 분석(time series analysis)
- 시계열(시간의 흐름에 따라 기록된 것) 자료(data)를 분석하고 여러 변수들간의 인과관계를 분석하는 방법
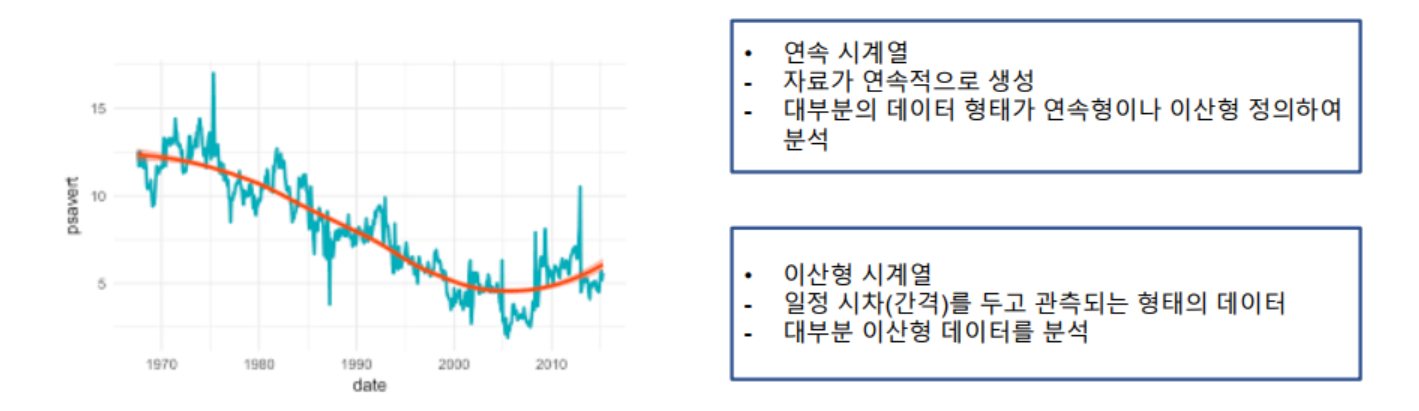
- 시계열 데이터
- 시계열 데이터는 시간을 기준으로 관측된 데이터로, 보통 일->주->월->분기->년 또는 Hour 등 시간의 경과에 따라서 관측한 데이터 - Ex) GDP, 주가, 거래액, 매출액, 승인금액 등을 시간에 흐름에 따라 정의한 데이터
- 시계열 데이터는 연속 시계열과 이산 시계열 데이터로 구분할 수 있음
- 시계열 분석의 목적
- 예측: 금융시장 예측, 수요 예측등 미래의 특정 시점에 대한 관심의 대상(반응변수)을 예측
- 시계열 특성 파악: 경향(Trend), 주기, 계절성, 변동성(패턴) 등 관측치의 시계열 특성 파악
- 전통 적인 시계열 분석 방법
- 자기 상관 모형(Autocorrelation, AR) : 변수의 과거 값의 선형 조합을 이용하여 예측하는 방법
- 이동 평균 모형(moving average, MA) : 최근 데이터의 평균을 예측치로 사용하는 방법
- ARIMA(Autoregressive Integrated Moving Average) : 관측값과 오차를 사용해서 모형을 만들어서 미래를 예측하는 방법
- 지수평활법 : 현재에 가까운 시점에 가장 많은 가중치 주고 멀어질수록 낮은 가중치를 주어서 미래를 예측하는 방법
- 시계열 요소
- 경향/추세(trend)
- 시계열 데이터가 장기적으로 증가(감소)할 때, 추세가 존재함
- 계절성(seasonality)
- 특정기간(1년 마다) 어떤 특정한 때나 1주일마다 특정 요일에 나타나는 것 같은 계절성 요인이 시계열에 영향을 줄 때 계절성(seasonality)이라고 함
- Ex) 패션업종 매출, 요일 별 온라인 쇼핑몰 매출 등이 계절성의 대표적
- 주기성(cycle)
- 일정한 주기(진폭)마다 유사한 변동이 반복되는 현상, 보통 경기 순환(business cycle)과 관련이 있으며 지속기간은 2년 임
- Ex) 주가 업좀별 개별(업종) 주가
- 불규칙요인(Irregular movements)
- 예측하거나 제어할 수 없는 요소
- Ex) 회귀분석의 오차와 같은 항목

- 경향/추세(trend)
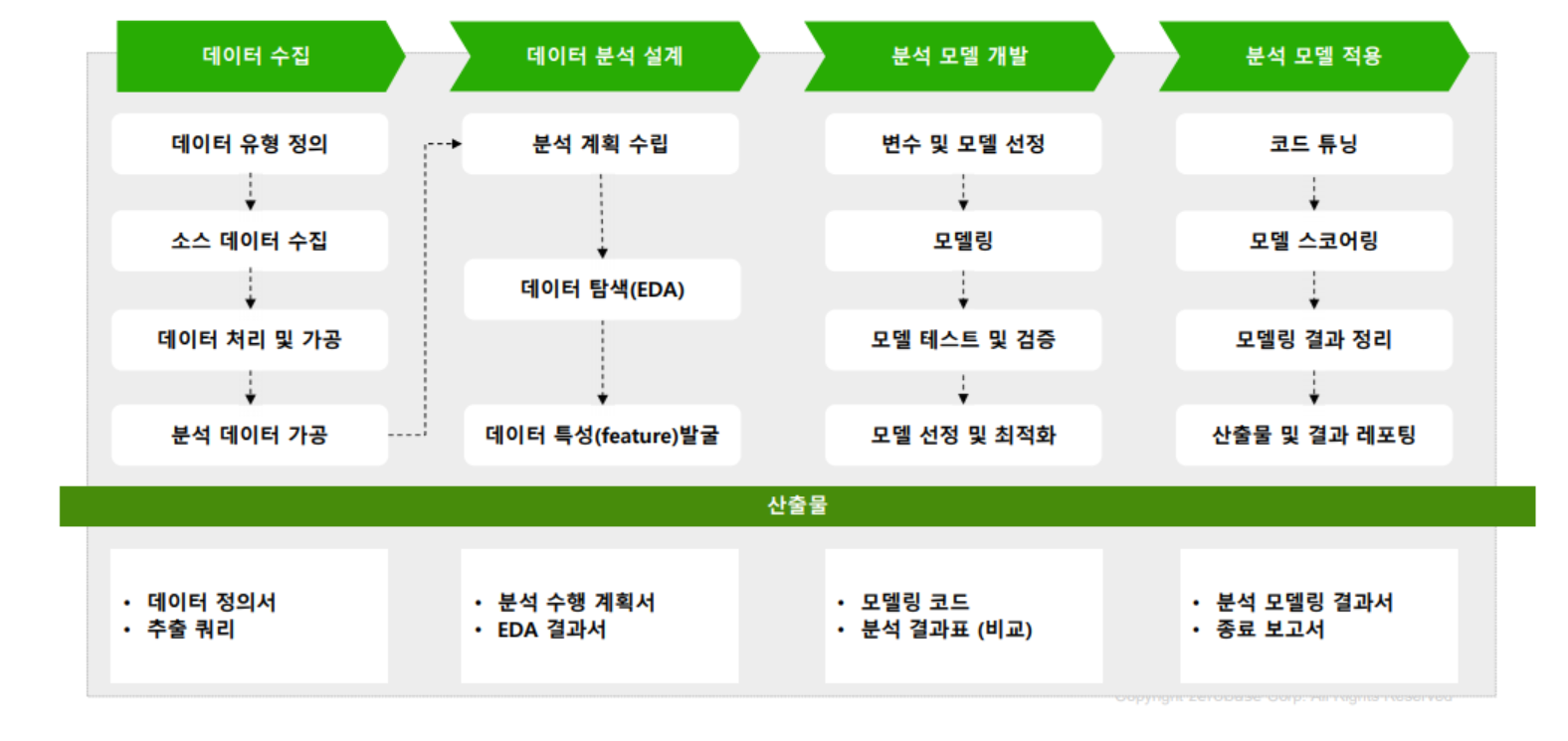
데이터 분석 순서도
"이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다."