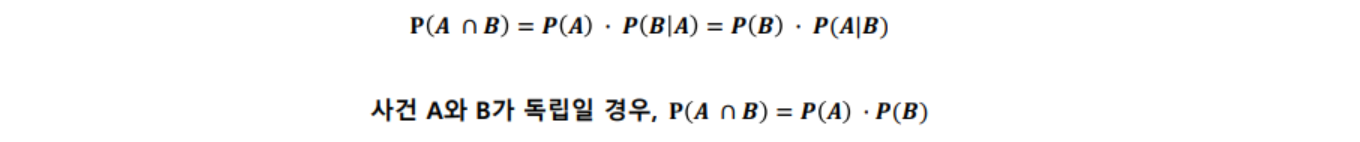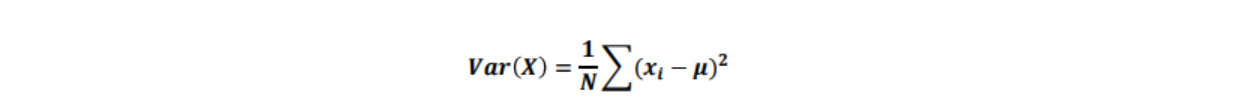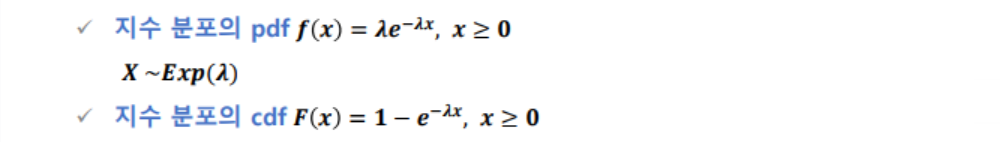✔️ 통계 기초 1~3
통계학
- 기술통계학(descriptive statistics) : 데이터를 수집하고 수집된 데이터를 쉽게 이해하고 설명할 수 있도록 정리 요약 설명하는 방법론
- 추론통계학(inferential statistics) : 모집단으로 부터 추출한 표본 데이터를 분석하여 모집단의 여러가지 특성을 추측하는 방법론
데이터와 그래프
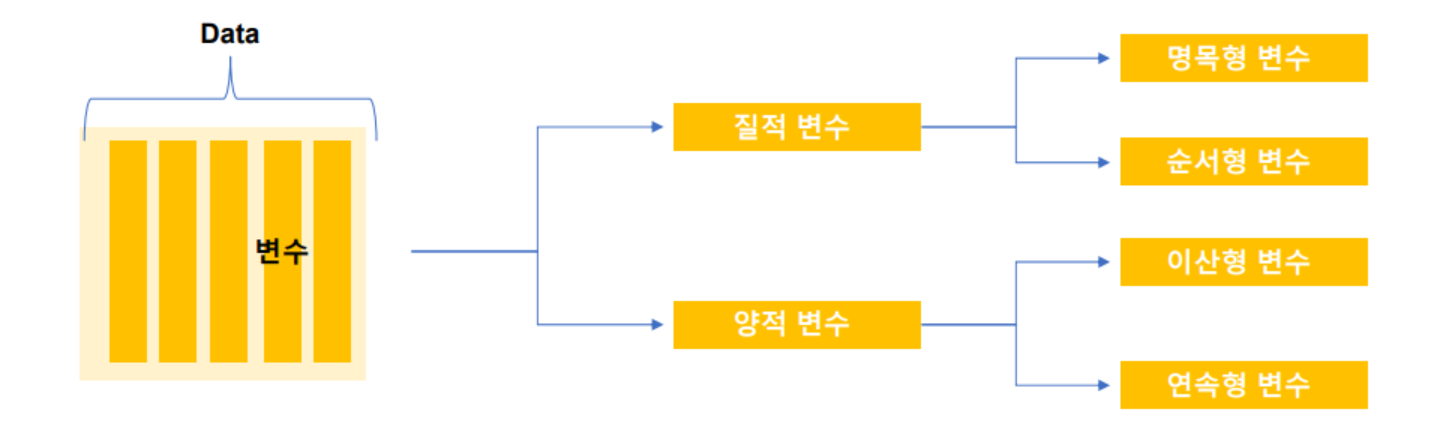
- 변수(Variable)
- 수학 변수 : 어떤 정해지지 않은 임의의 값을 표현하기 위해 사용된 '기호' (변하는 숫자)
- 통계학 변수 : 조사 목적에 따라 관측된 자료값,
- 자료(Data) : 해당 변수에 대하여 관측된 값
- 질적 자료
- 관측된 데이터가 성별, 주소지(시군구), 업종 등과 같이 몇 개의 범주로 구분하여 표현할 수 있는 데이터를 의미
- 데이터 입력시 1은 남자, 2는 여자로 표현 가능하나 여기서 숫자의 의미는 없음
- 양적 자료
- 관측된 데이터가 숫자의 형태로 숫자의 크기가 의미를 갖고 있음
- 숫자를 표현할 때는 이산형 데이터와 연속형 데이터로 구분할 수 있음
- EDA(Exploratory Data Analysis)
- 데이터를 탐색하는 분석 방법으로 도표, 그래프, 요약 통계 등을 사용하여 데이터를 체계적으로 분석하는 하나의 방법
- 목적
- 데이터 분석 프로젝트 초기에 가설을 수립하기 위해 사용
- 데이터 분석 프로젝트 초기에, 적절한 모델 및 기법의 선정
- 변수 간 트렌드, 패턴, 관계 등을 찾고 통계적 추론을 기반으로 가정을 평가
- 분석 데이터에 적절한가 평가, 추가 수집, 이상치 발견 등에 활용
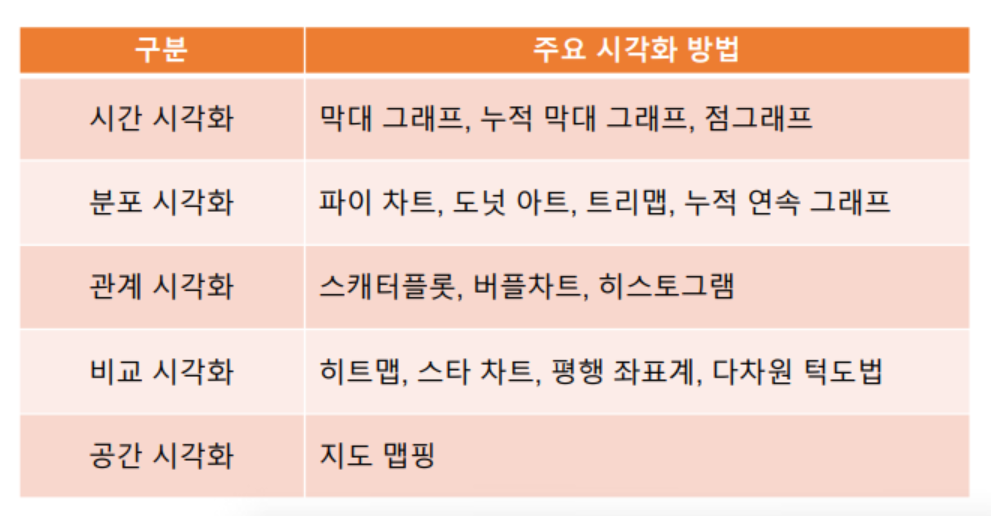
- 데이터 시각화
- 데이터 분석 결과를 쉽게 이해할 수 있도록 시각적으로 표현하고 전달되는 과정
- 목적 : 정보를 명확하고 효과적으로 전달하는 것
기초 통계량
- 기초 통계량
- 통계량(statistic)은 표본으로 산출한 값으로, 기술 통계량이라고도 표현함
- 통계량을 통해 데이터(표본)가 갖는 특성을 이해 할 수 있음
- 중심 경향치
- 표본(데이터)를 이해하기 위해서는 표본의 중심에 대해서 관심을 갖기 때문에 표본의 중심을 설명하는 값을 대표값이라 하며 이를 중심경향치라고 함
- 대표적인 중심 경향치는 평균이며, 중앙값, 최빈값, 절사 평균 등이 있음
- 평균
- 표본으로 추출된 표본 평균(sample mean)이라고하며, 모집단의 평균을 모평균이라고 함
- 중앙값(median)
- 평균과 같이 자주 사용하는 값으로 표본으로 부터 관측치를 크기순으로 나열 했을 때, 가운데 위치하는 값을 의미
- 관측치가 홀수 일 경우 중앙에 취하는 값이고, 짝수 일 경우 가운데 두개의 값을 산술 평균한 값임
- 이상치가 포함된 데이터에 대해서 사용함
- 최빈값(mode)
- 관측치 중에서 가장 많이 관측되는 값
- 산포도
- 데이터가 어떻게 흩어져 있는지를 확인하기 위해서는 중심경향치와 함께 산포에 대한 측도를 같이 고려해야 함
- 측도 : 범위, 사분위수, 분산, 표준편차, 변동 계수 등이 있음
- 범위(Range)
- 데이터의 최대값과 최소값의 차이를 의미함
- 사분위수(quartile)
- 전체 데이터를 오름차순으로 정렬하여 4등분을 하였을 때, 첫 번째를 제1사분위수(Q1), 두 번째를 제2사분위수(Q2), 세 번째를 제3사분위수(Q3)이라고 함
- 사분위수 범위(interquartile range): IQR = 제 3사분위수(Q3) – 제1사분위수(Q1)
- 백분위수(percentile)
- 전체 데이터를 오름차순으로 정렬하여 주어진 비율에 의해 등분한 값을 말하며, 제p백분위수는 p%에 위치한 자료 값을 말함
- 분산(variance)
- 데이터의 분포가 얼마나 흩어져 있는지를 알 수 있는 측도 임
- 데이터의 각각의 값들의 편차 제곱합으로 계산하며 수식은 아래와 같음
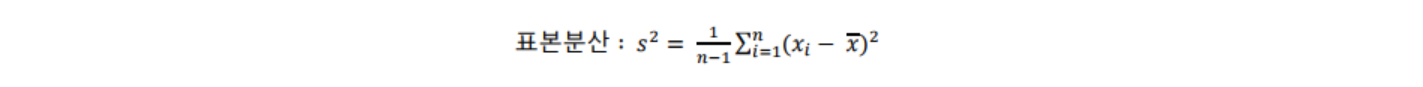
- 표준 편차(standard deviation)
- 분산의 제곱근으로 정의하며 수식은 아래와 같음

- 분산의 제곱근으로 정의하며 수식은 아래와 같음
- 분산
- 크기가 N인 모집단의 평균을 라고 할 때 모평균과 모분산은 다음과 같음
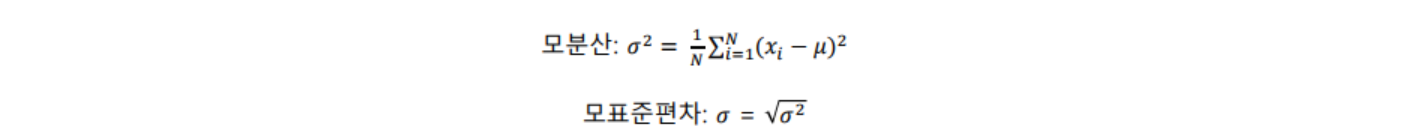
- 크기가 N인 모집단의 평균을 라고 할 때 모평균과 모분산은 다음과 같음
- 변동계수(Coefficient of Variation: CV)
- 평균이 다른 두개 이상의 그룹의 표준편차를 비교할 때 사용함
- 변동계수는 표준편차를 평균으로 나누어서 산출하여 단위나 조건에 상관 없이 서로 다른 그룹의 산포를 비교하며 실제 분석에서 자주 사용함
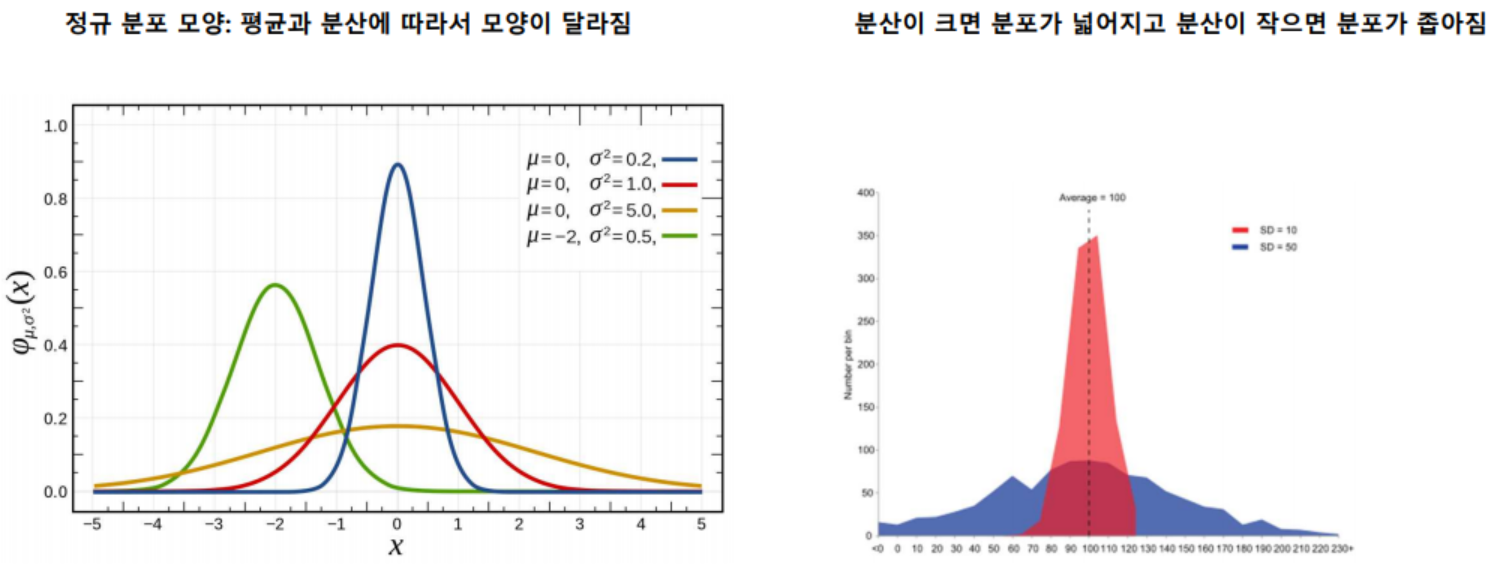
- 왜도
- 자료의 분포가 얼마나 비대칭적인지 표현하는 지표임 왜도가 0이면 좌우가 대칭이고, 0에서 클수록 우측꼬리가 길고 0에서 작을수록 좌측 꼬리가 김
- 첨도
- 확률분포의 꼬리가 두꺼운 정도를 나타내는 척도임 첨도값(K)이 3에 가까우면 산포도가 정규분포에 가까움
- 3보다 작을 경우에는(K<3) 산포는 정규분포보다 꼬리가 얇은 분포로 생각할 수 있다, 첨도값이 3보다 큰 양수이면(K>3) 정규분포보다 꼬리가 두꺼운 분포로 판단
확률
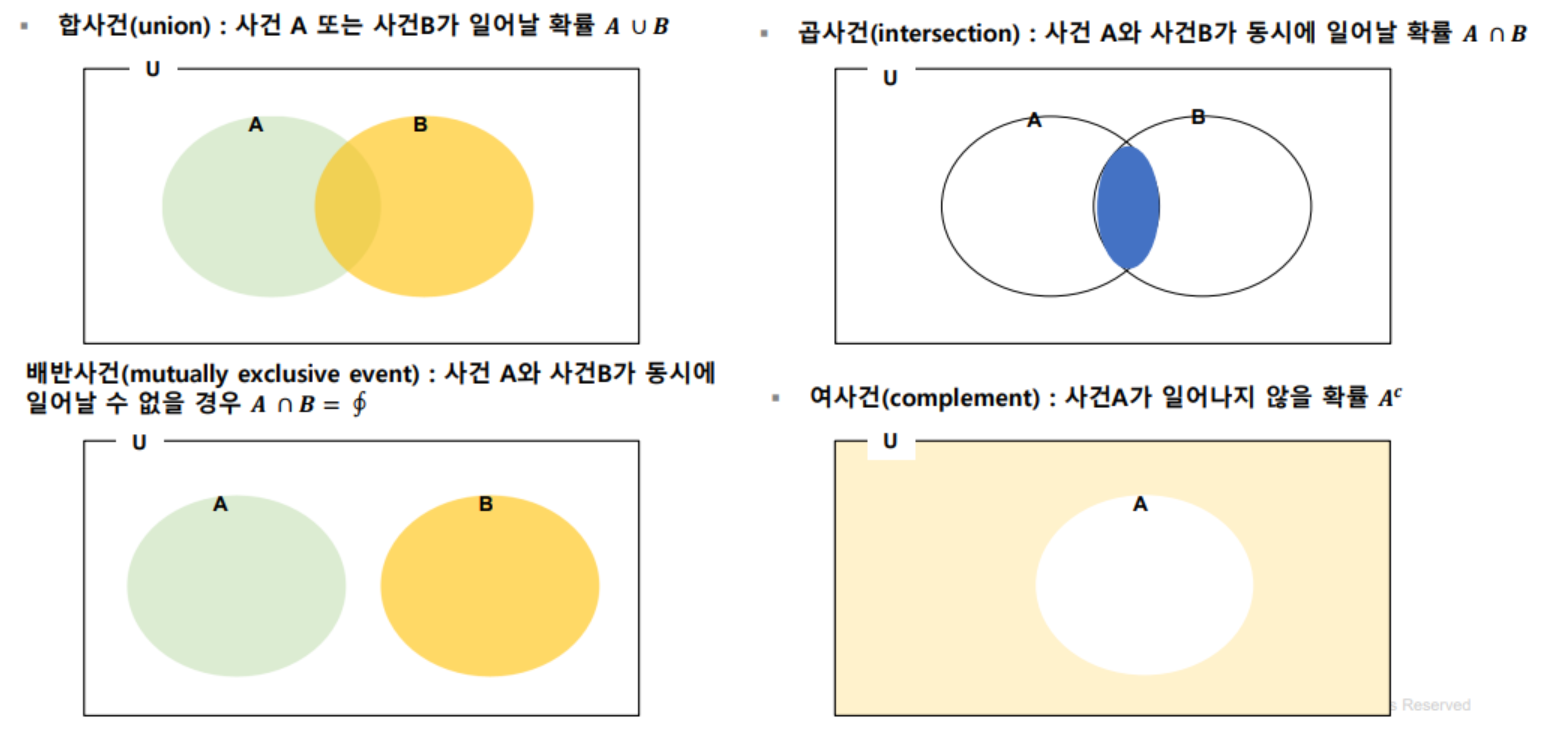
- 확률(probability)
- 모든 경우의 수에 대한 특정 사건이 발생하는 비율
- 표본 공간(Sample Space)
- 어떤 실험에서 나올 수 있는 모든 가능한 결과들의 집합
- 동전 던지기의 경우 S = {앞면, 뒷면}, 주사위던지기 S = {1,2,3,4,5,6}
- 사건 A가 일어날 확률을 P(A)라고 하고, 표본 공간(S)가 유한집합일때 표본 공간의 모든 원소들이 일어날 확률이 같으면

- 확률의 성질

- 순열과 조합

- 조건부확률(conditional probability)
- 어떤 사건A가 발생한 상황에서(주어졌을때) 또 하나의 사건 B가 발생할 확률
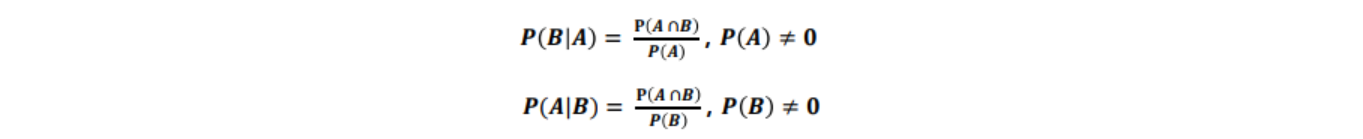
- 어떤 사건A가 발생한 상황에서(주어졌을때) 또 하나의 사건 B가 발생할 확률
- 확률의 곱셈법칙
- 베이즈 정리(Bayes’ Theorem)
- 표본 공간 S에서 서로 배반인 사건 6, 6, … , 6K에 의하여 분할 되어 있을때, 임의의 사건 A에 대하여 다음이 성립

- 표본 공간 S에서 서로 배반인 사건 6, 6, … , 6K에 의하여 분할 되어 있을때, 임의의 사건 A에 대하여 다음이 성립
확률 변수
- 확률 변수(random variable) : 표본공간에서 각 사건에 실수를 대응시키는 함수
- 확률 변수의 평균(=기대값)
- 확률 변수의 분산
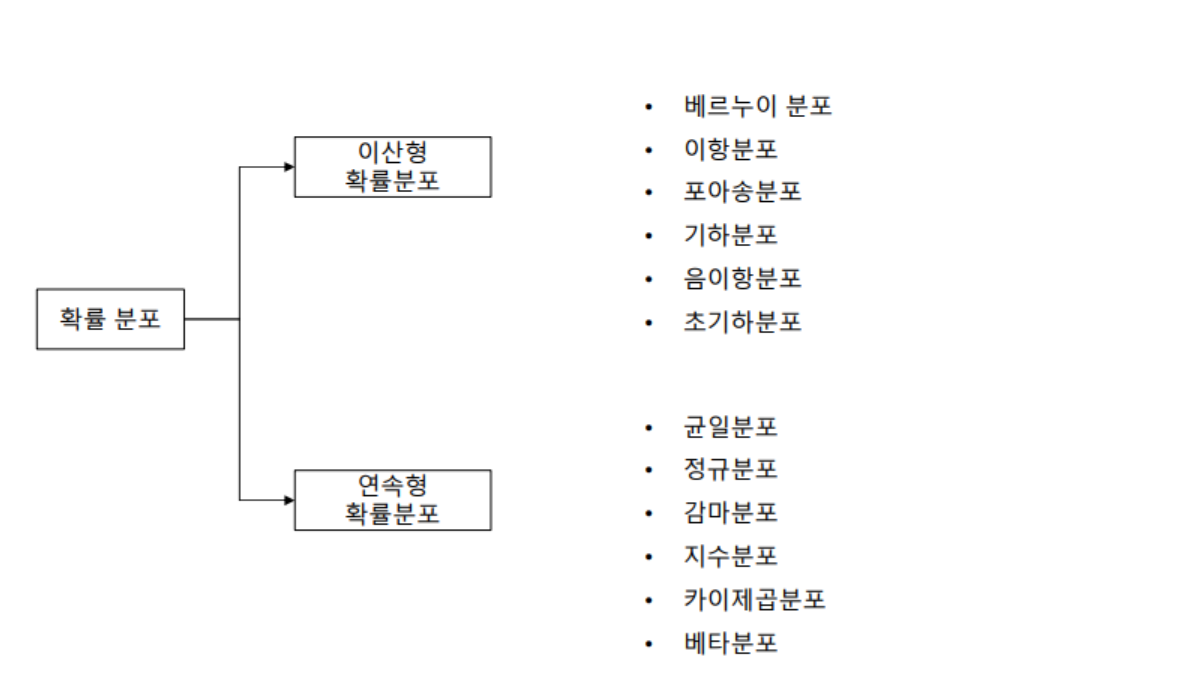
확률 분포
- 확률 분포(probability distribution) : 확률 변수 X가 취할 수 있는 모든 값과 그 값을 나타날 확률을 표현한 함수
1. 이산형 확률 분포

- 이산형 균등 분포(discrete uniform distribution) : 확률 변수 X가 유한개이고, 모든 확률 변수에 대하여 균일한 확률을 갖는 분포를 이산형 균등 분포라고 함
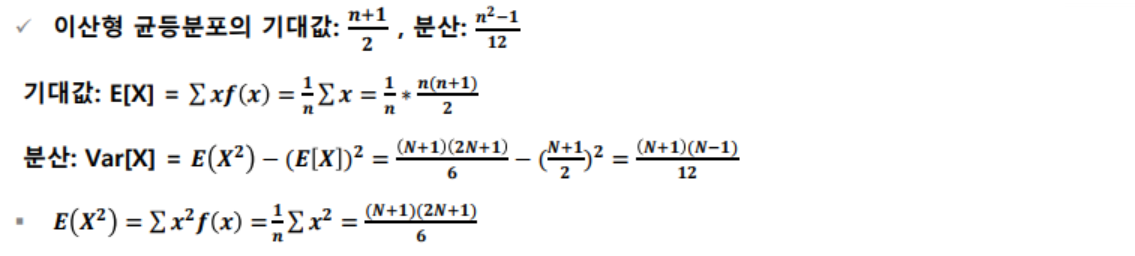
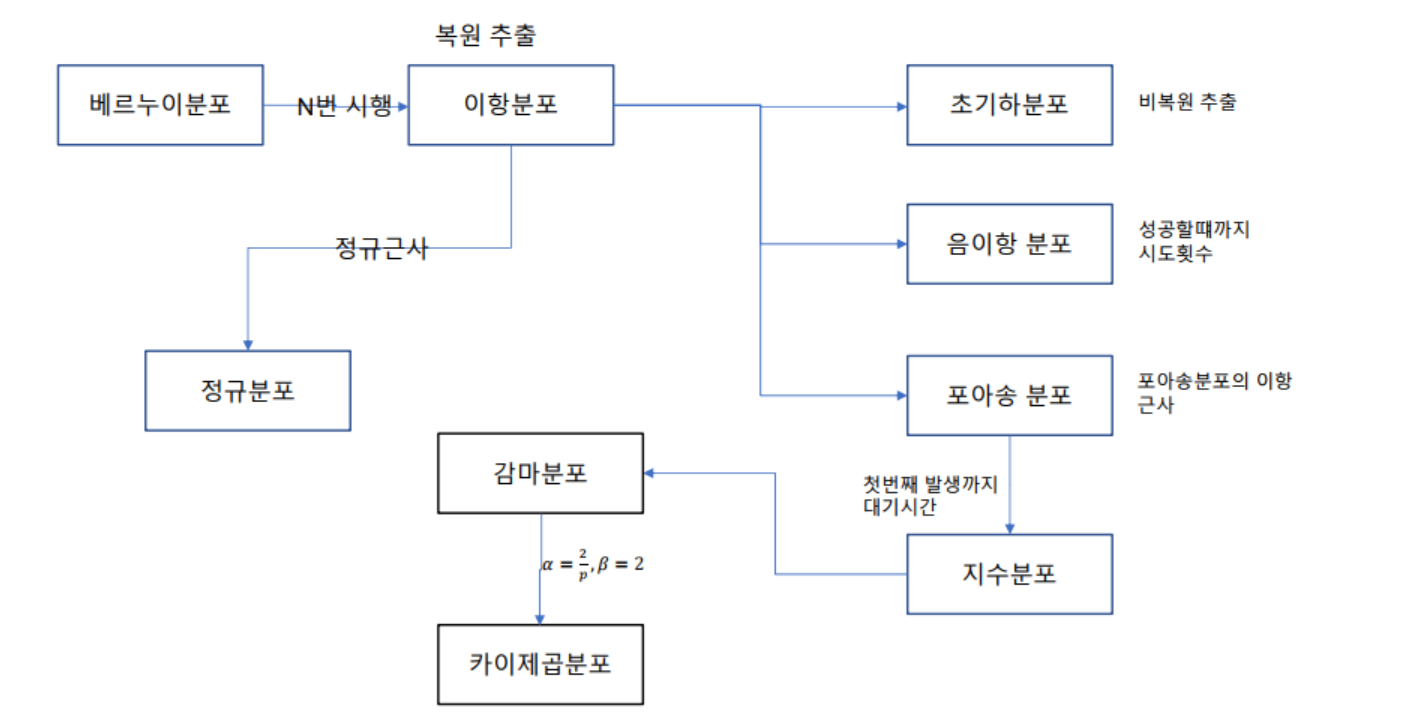
- 베르누이 분포(Bernoulli distribution) : 베르누이 시행에서 성공이 ‘1’, 실패가 ‘0’의 값을 갖을 때 확률 변수 X의 분포
- 베르누이 시행(Bernoulli trial) : 각 시행의 결과가 성공, 실패 두가지 결과만 존재하는 시행

- 베르누이 시행(Bernoulli trial) : 각 시행의 결과가 성공, 실패 두가지 결과만 존재하는 시행
- 이항분포(Binomial distribution) : 연속적인 베르누이 시행을 거처 나타나는 확률 분포
- 서로 독립인 베르누이 시행을 n번 반복해서 실행 했을 때, 성공한 횟수 X의 확률 분포
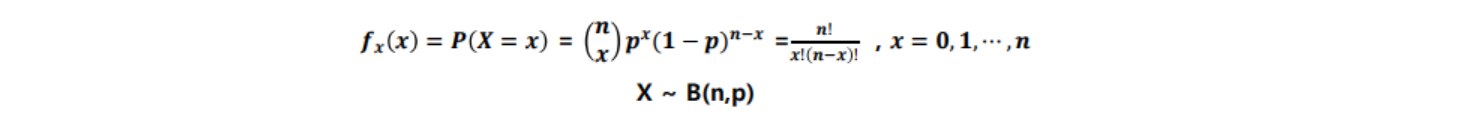


- 서로 독립인 베르누이 시행을 n번 반복해서 실행 했을 때, 성공한 횟수 X의 확률 분포
- 포아송 분포(Poisson distribution) : 어느 희귀한 사건이 어떤 일정한 시간대에 특정한 사건이 발생할 확률 분포

- 기하분포(geometric distribution) : 어떤 실험에서 처음 성공이 발생하기 까지 시도한 횟수 X의 분포, 이때 각 시도는 베르누이 시행을 따름
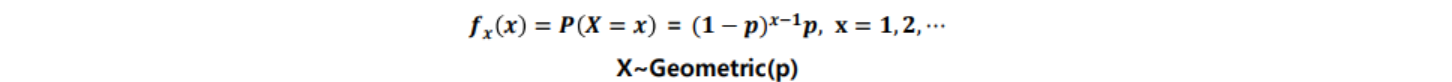

- 음이항분포(negative binomial distribution) : 어떤 실험에서 성공확률이 p일 때, r번의 실패가 나올 때 까지 발생한 성공 횟수 X의 확률 분포
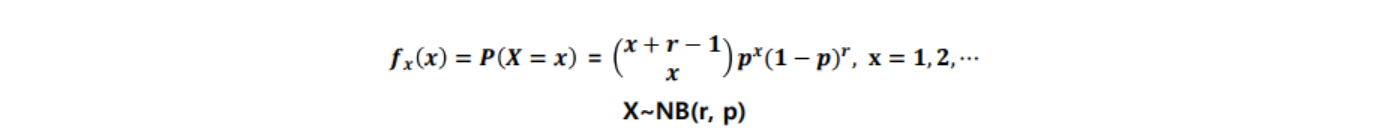

2. 연속형 확률 분포
- 확률밀도함수(probability density function, pdf) : 연속형 확률 변수 X에 대해서 함수 q가 아래의 조건을 만족하면 확률밀도함수라고 함
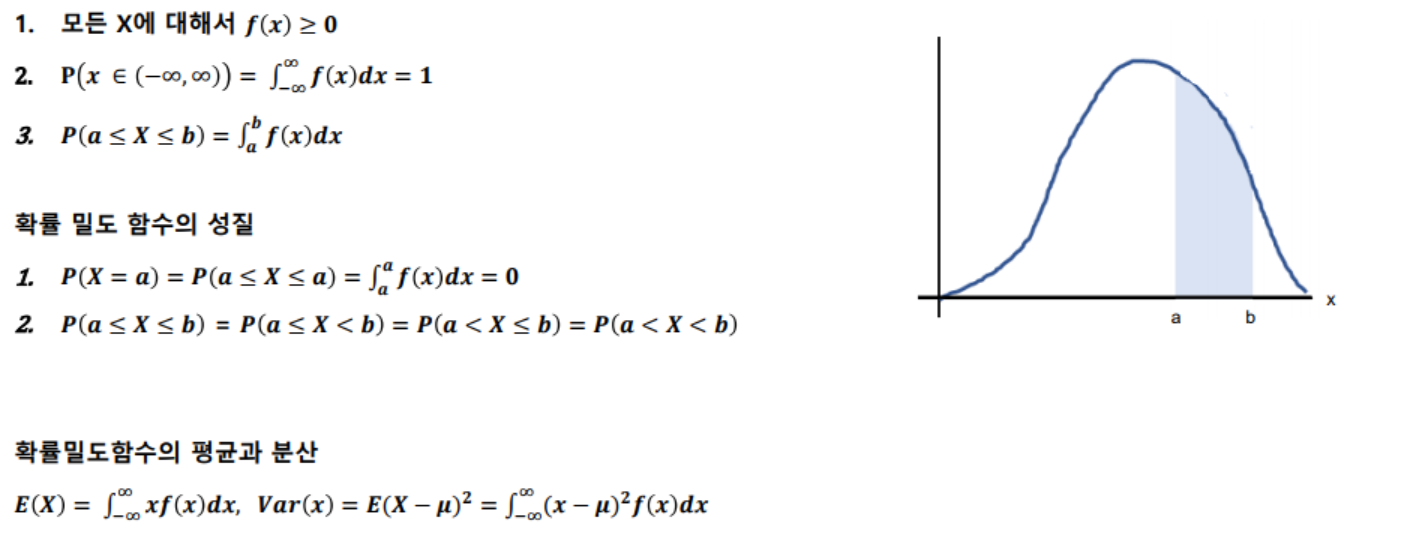
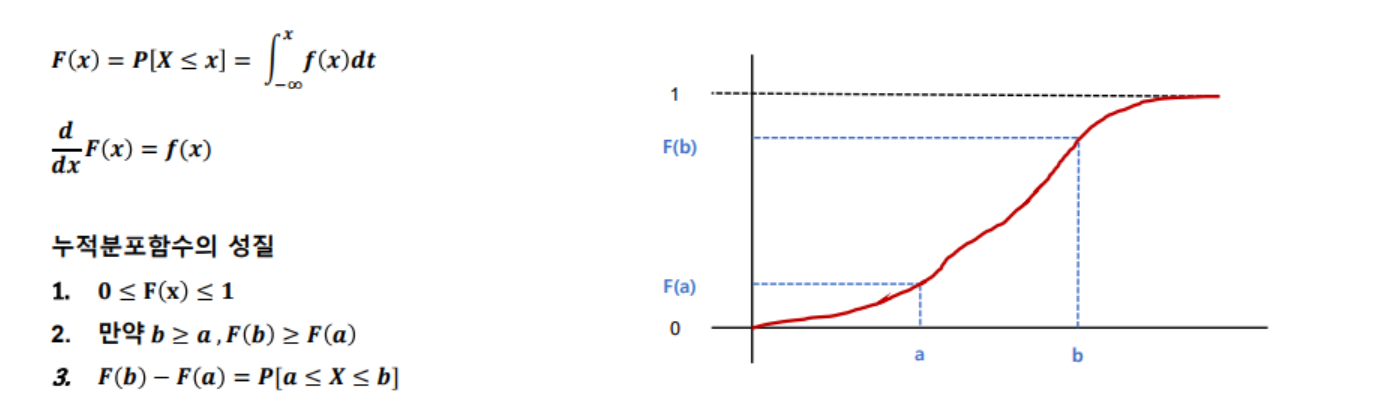
- 누적분포함수(cumulative density function, cdf): 확률밀도함수를 적분하면 누적분포함수가 됨
- 균일분포(uniform distribution) : 확률 변수가 X가 a와 b사이에서 아래와 같은 확률 밀도 함수(pdf)를 같음
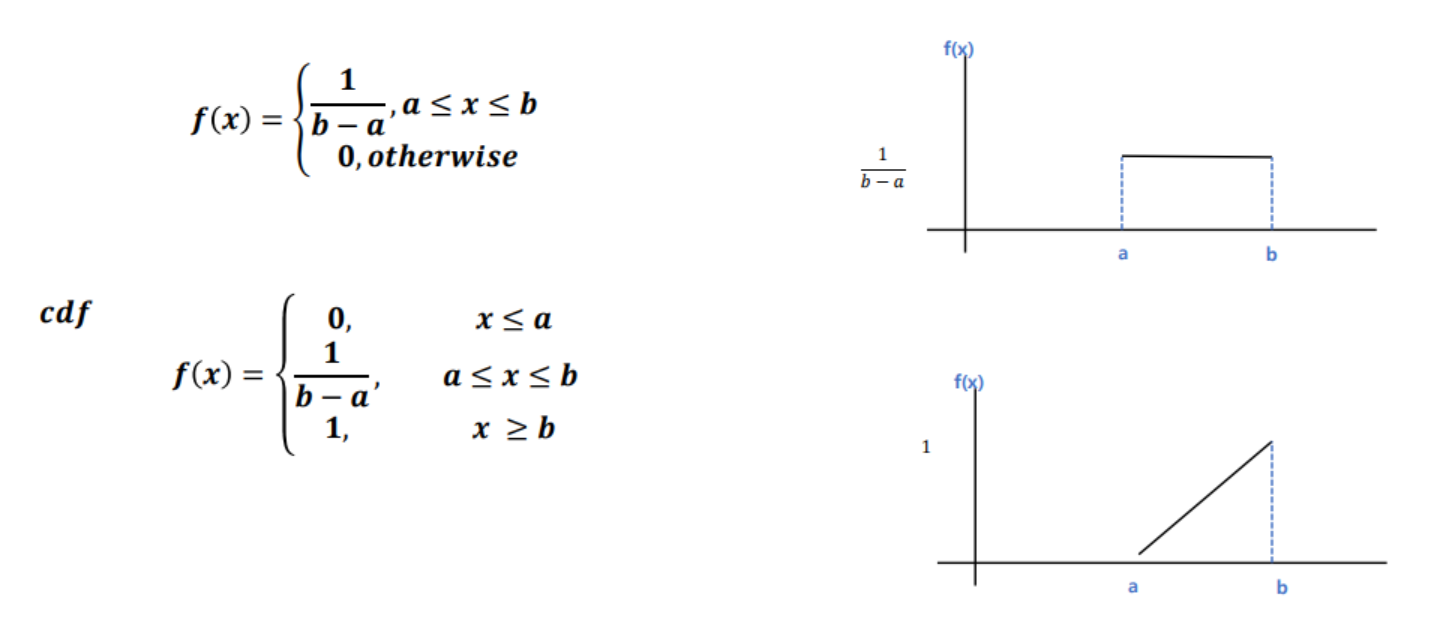
- 균일 분포의 평균, 분산 유도식
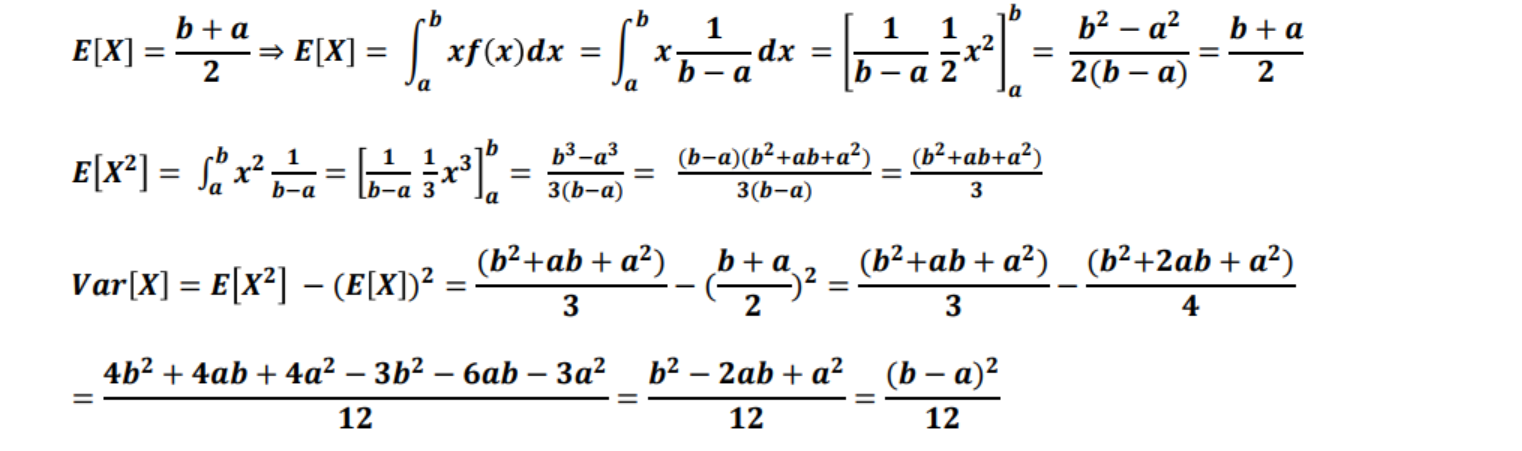
- 균일 분포의 평균, 분산 유도식
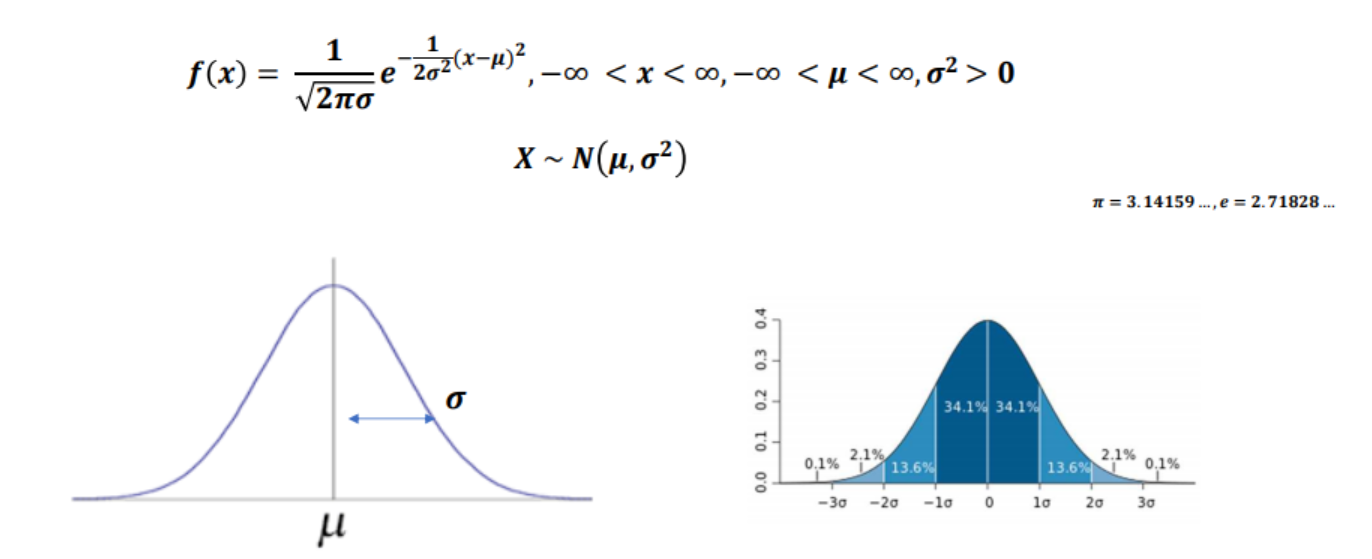
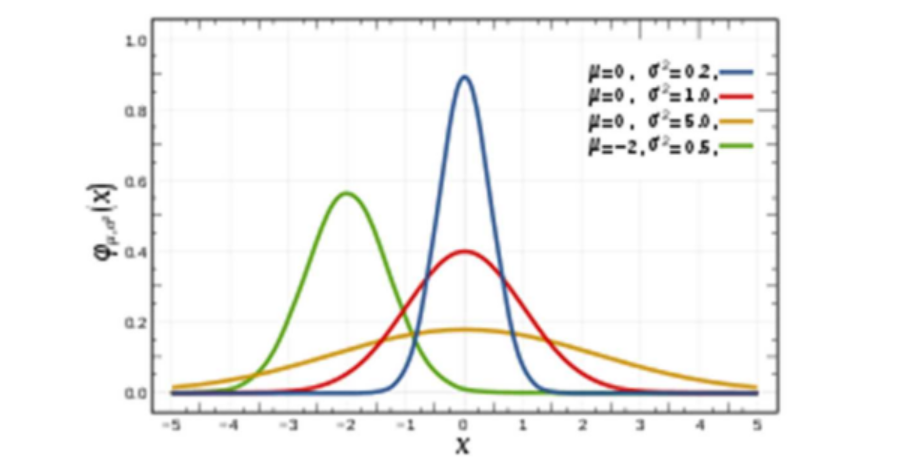
- 정규분포(normal distribution, 가우스 분포) : 확률 밀도 함수는 확률 변수 X가 평균이 µ이고, 분산이 σ²인 정규분포를 따를 때 아래와 같음
- 정규분포의 평균과 분산
- 평균 : E[x] = µ
- 분산 : Var[X] = σ², 표준편차 : σ
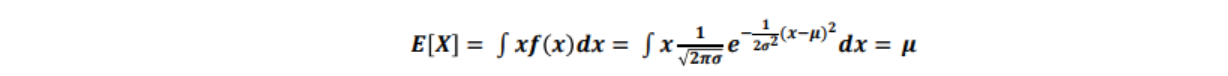
- 표준 정규 분포(standard normal distribution) : 확률 변수 X ~ N(µ, σ²) 정규 분포를 따르고, 확률 변수 Z = (X-µ)/σ 라고 할 때 확률변수 Z ~ N(0, 1)
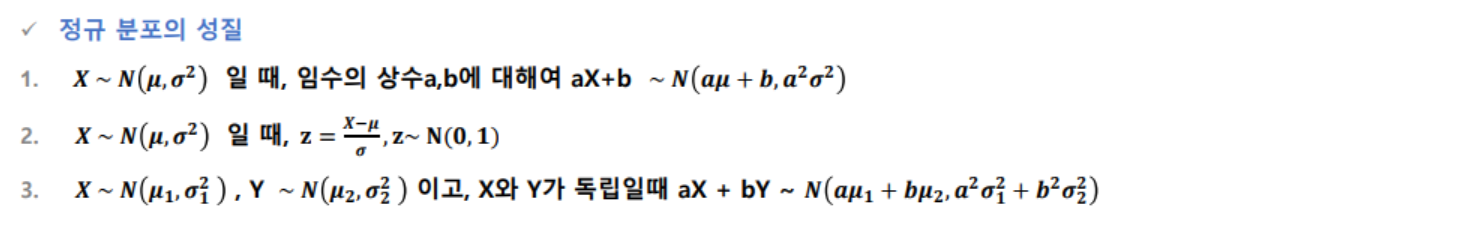
- 이항분포의 정규 근사 : X~B(n,p) 일 때, 확률변수 X는 n이 충분히 크면 근사적으로 정규 분포 X~N(np, np(1-np))를 따름
- 정규분포의 평균과 분산
- 지수분포(exponential distribution) : 단위 시간당 발생할 확률 ⁁인 어떤 사건의 횟수가 포아송 분포를 따르다면, 어떤 사건이 처음 발생 할때까지 걸린 시간 확률 변수 X는 지수 분포임
- 확률 분포의 관계도
"이 글은 제로베이스 데이터 취업 스쿨의 강의 자료 일부를 발췌하여 작성되었습니다."