벡터
numpy
: numpy list는 행(row)이 기본단위이다.
벡터 연산
성분곱
: 각 성분을 곱한 연산
: 같은 모양끼리만 가능
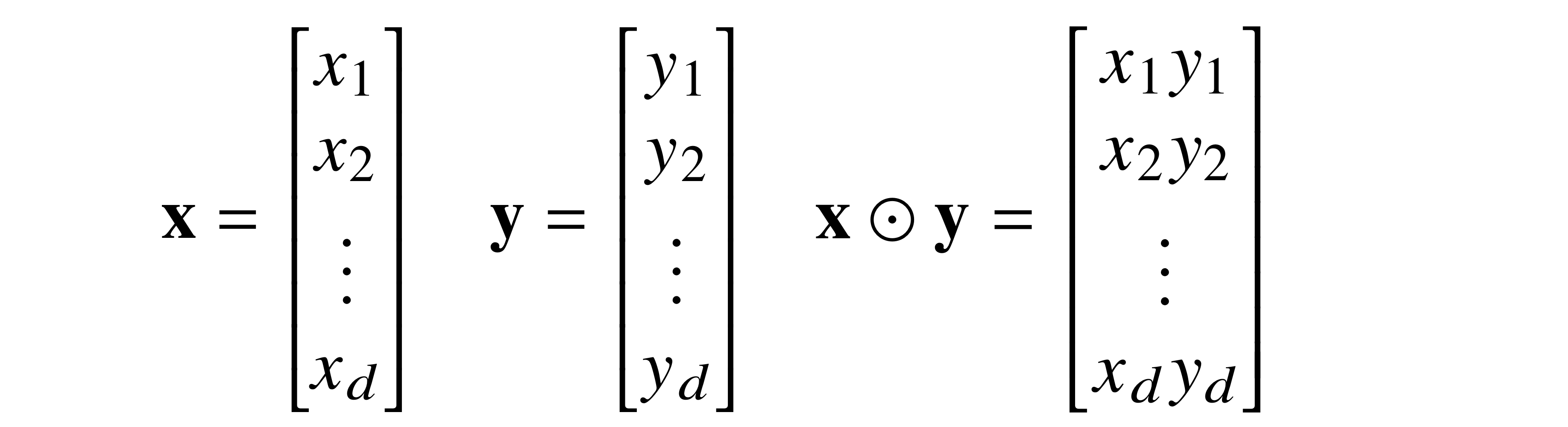
x = np.array([1,2,3])
y = np.array([5,2,1])
z = x*y # 벡터 성분곱내적
- y에 대한 x의 정사영에, ||y||만큼 곱한 값

- 두 벡터의 각 성분의 곱의 합
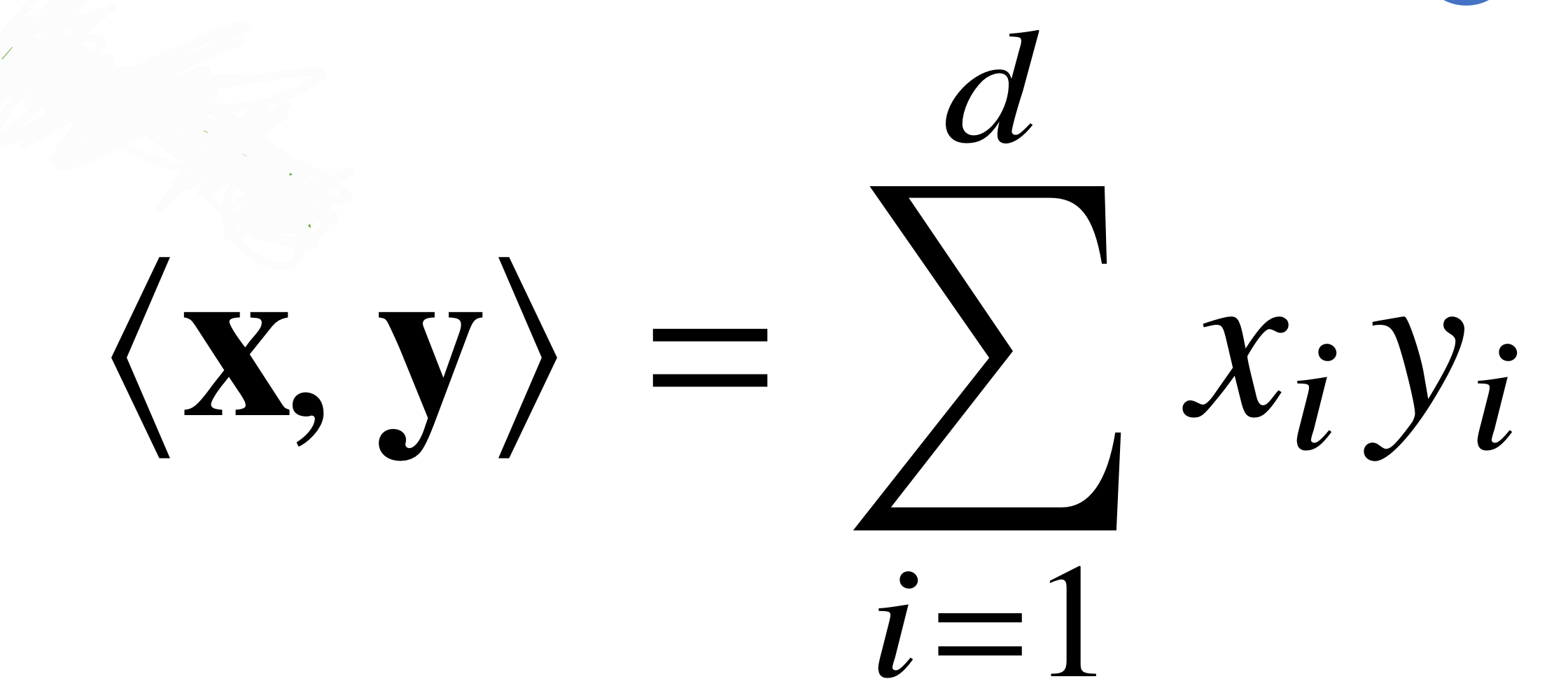
- 두 벡터 사이의 각도
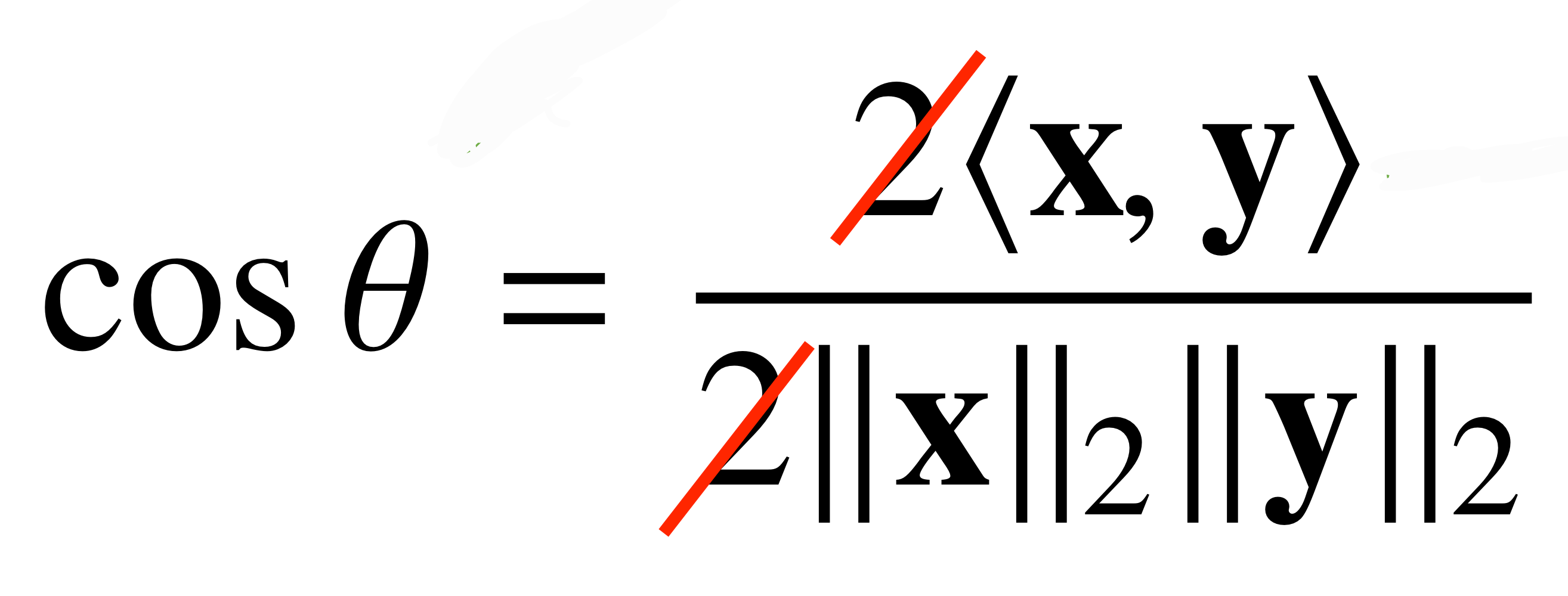
def angle(x,y):
v = np.inner(x, y) / (l2_norm(x) * l2_norm(y)
theta = np.arccos(v)
return thetaNorm
- 벡터의 원점부터의 거리
- ||x|| : norm 기호
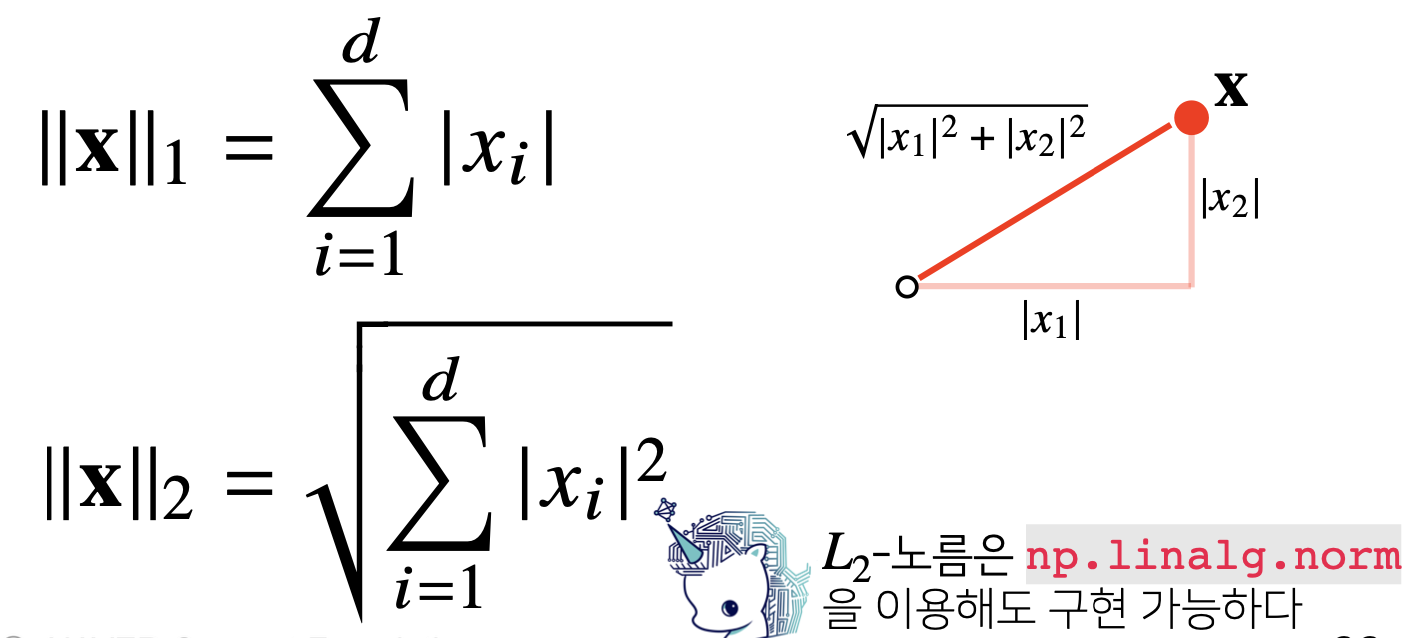
L1-norm
- 모든 성분의 절대값 합
- ||x||1
L2-norm
- 유클리드 거리(피타고라스 정리)
: 직선거리 - ||x||2
def l1_norm(x):
norm_x = np.abs(x)
norm_x = np.sum(norm_x)
return norm_x
def l2_norm(x):
norm_x = x*x
norm_x = np.sum(norm_x)
norm_x = np.sqrt(norm_x)
return norm_xnorm에 따른 원
- norm의 종류에 따라 기하학적 성질이 달라진다.
- 원 : 원점으로부터 거리가 같은 점들의 집합
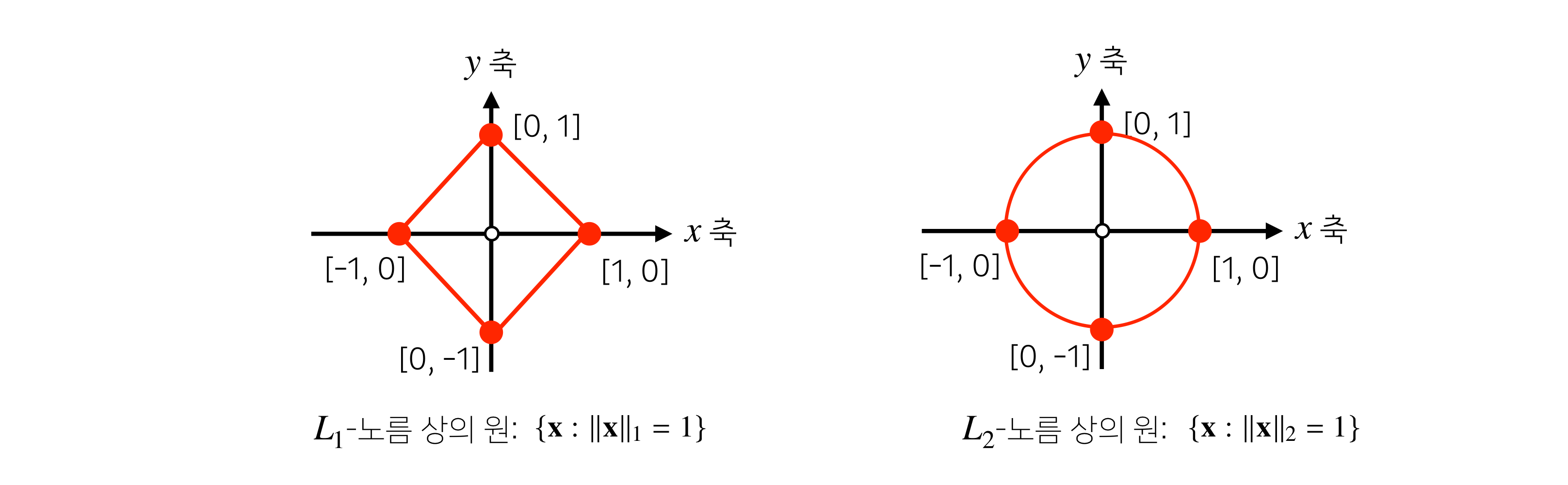
행렬
행렬의 연산
성분곱
: 벡터와 같이 각 인덱의 위치끼리 곱한 결과 (같은 형태의 벡터끼리만 가능)
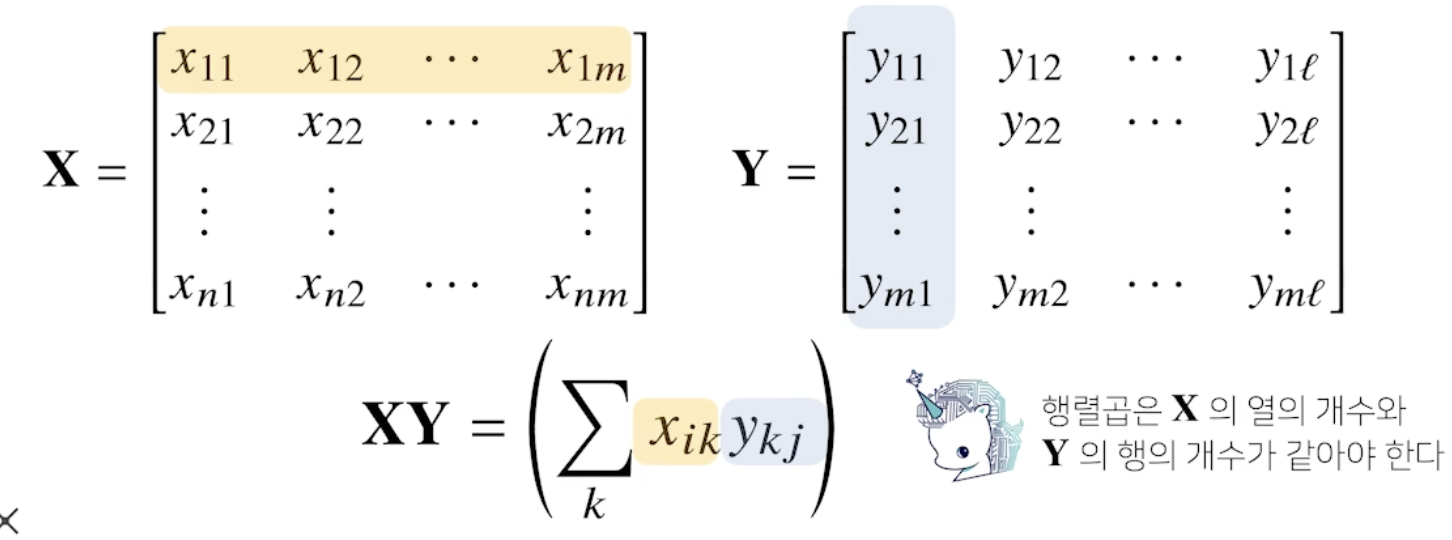
행렬곱 = np.matmul()
- XY
: X행렬의 i번째 행벡터와 Y행렬의 j번째 열벡터의 내적을 성분으로 가지는 행렬 - X의 행벡터 크기와 Y의 열벡터 크기가 같아야한다.
- numpy에서 @ 연산자로 연산 가능
x = np.array([[1,-2,3], [7,5,0], [-2,-1,2]])
y = np.array([[0,1], [1,-1], [-2,1]])
print(x @ y)
# [[-8 6]
# [ 5 2]
# [-5 1]]행렬의 내적
- 행렬의 다양한 표현
(numpy에서는 행이 기본 단위이기 때문에 y에 transpose를 하는게 맞다.)
(아래 그림에서는 열이 기본단위인 수식)
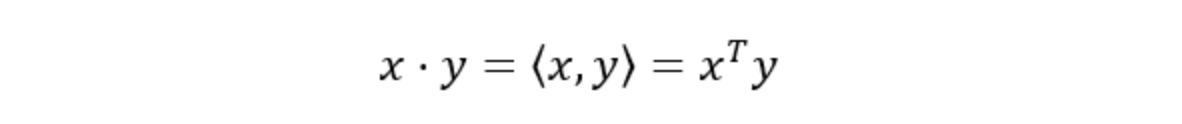
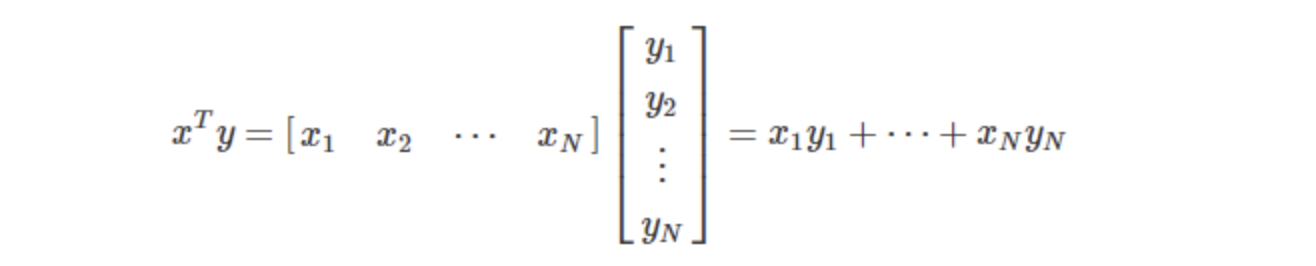
np.inner
- X(Y^T)
: 행렬X와 행렬Y-transpose의 행렬곱 - 두 행렬의 행벡터 크기가 같아야 한다. (열의 size가 같아야 한다.)
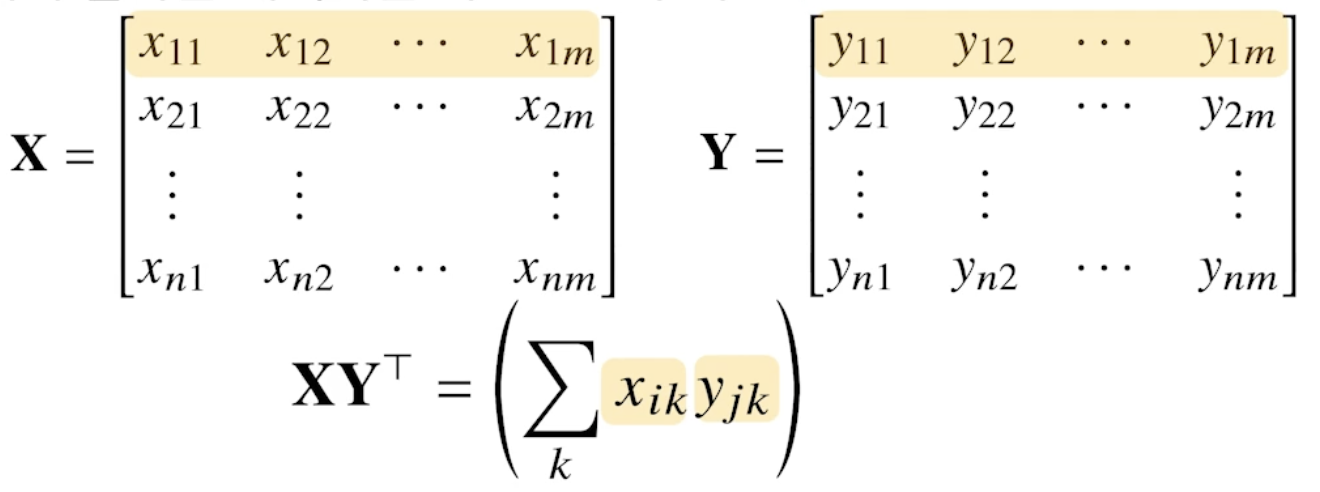
- numpy에서의 행렬 내적 : np.inner
- X행렬의 i번째 행벡터와 Y행렬의 j번째 행벡터의 내적을 성분으로 가지는 행렬
: 두 행렬의 행벡터로 연산을 하기 때문에 transpose하면 안된다.

- X행렬의 i번째 행벡터와 Y행렬의 j번째 행벡터의 내적을 성분으로 가지는 행렬
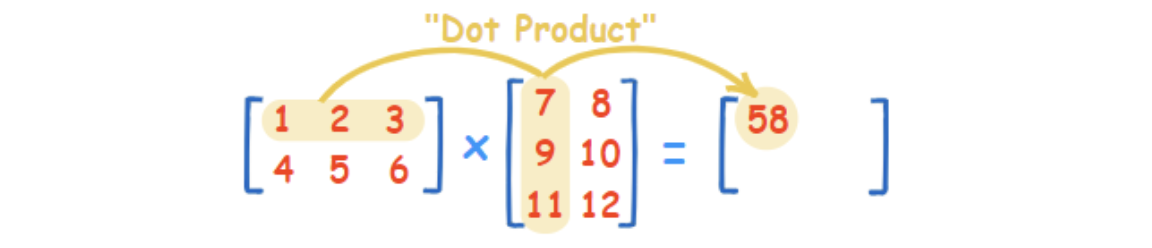
np.dot()
- np.dot(X, Y)
: X행렬의 i번째 행벡터와 Y행렬의 j번째 열벡터의 내적을 성분으로 가지는 행렬
1차원
- shape 정리 안 해줘도 된다.
X = np.array([1,2,3])
Y = np.array([1,2,3])
Z = np.array([[1],[2],[3]])
print(np.dot(X,Y))
# 14
print(np.dot(X,Z))
# [14]2차원
- 행렬곱(@) = np.matmul과 차이 없다.
- 행렬곱(@) = np.matmul 사용을 권장
- shape 정리 안 할시 오류 발생
: ( A x N) dot ( N x B )
A = np.array([[1,2,3],[4,5,6]])
B = np.array([[1,2],[3,4],[5,6]])
C = np.array([[1,2,3],[4,5,6]])
print(np.dot(A,B))
# array([[22, 28],
# [49, 64]])
print(np.dot(A,C))
# Errorn차원
- np.dot(X, Y)
: X의 마지막 axis와 Y의 마지막에서 두번째 axis간의 곱
:
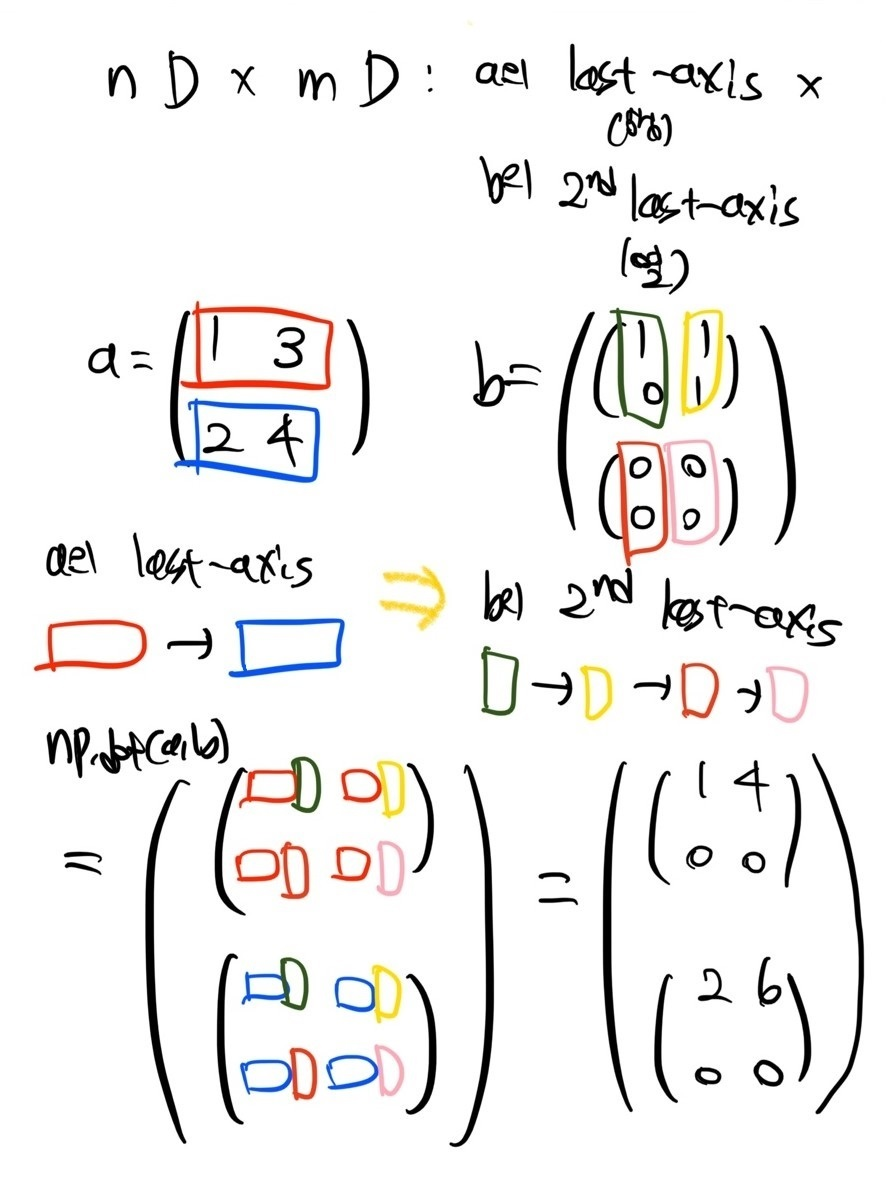

(출처 : https://jimmy-ai.tistory.com/75, https://seong6496.tistory.com/110)
np.matmul()
= 행렬곱@
n차원

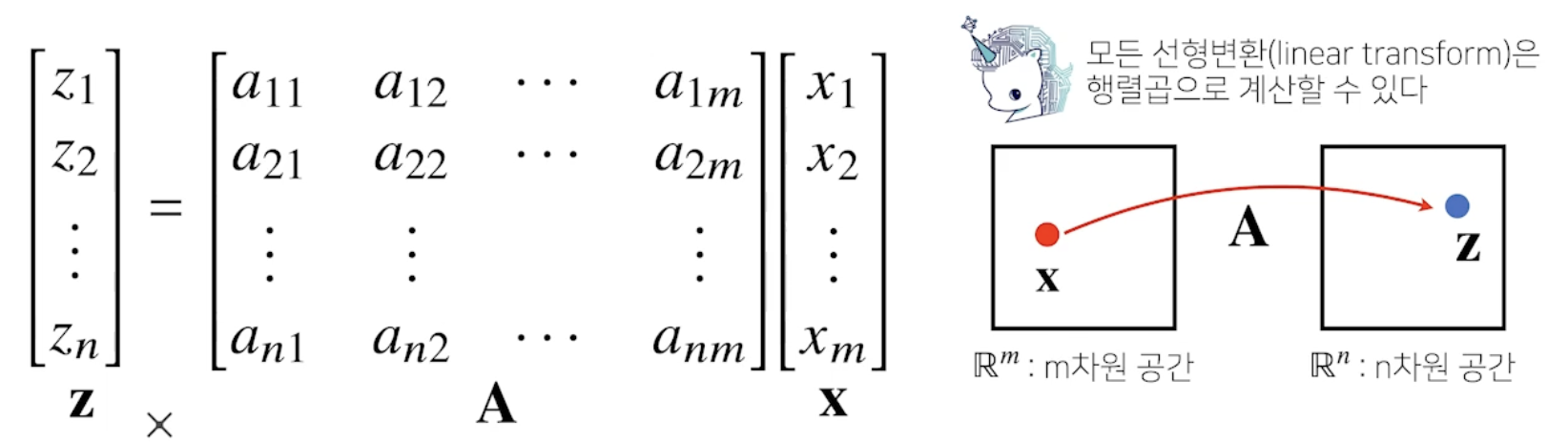
선형변환
선형변환
- 행렬이 벡터공간에서 연산자(operator)로 사용되는 경우
- 행렬곱을 통해 벡터를 다른 차원 공간으로 보낼 수 있다.
- 패턴을 추출하거나, 데이터를 압출할 수 있다.
역행렬
: 행렬A에 의한 연산(차원공간의 이동)을 거꾸로 되돌리는 연산
- 행과 열의 size가 같아야 한다.
- 행렬식(determinant)가 0이 아니어야 한다.
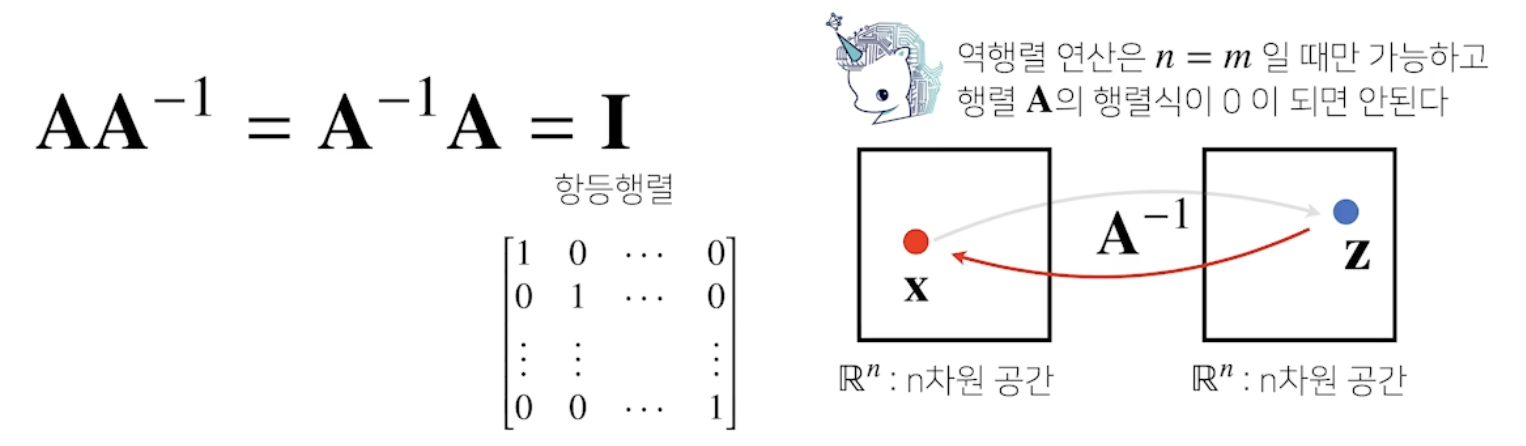
- numpy에서 역행렬 구하는 함수
: np.linalg.inv(X)
유사역행렬
-
무어펠로즈(Moore-Penrose)역행렬, 유사역행렬(Psudo-Inverse)
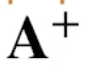

-
numpy 함수
: np.linalg.pinv(X) -
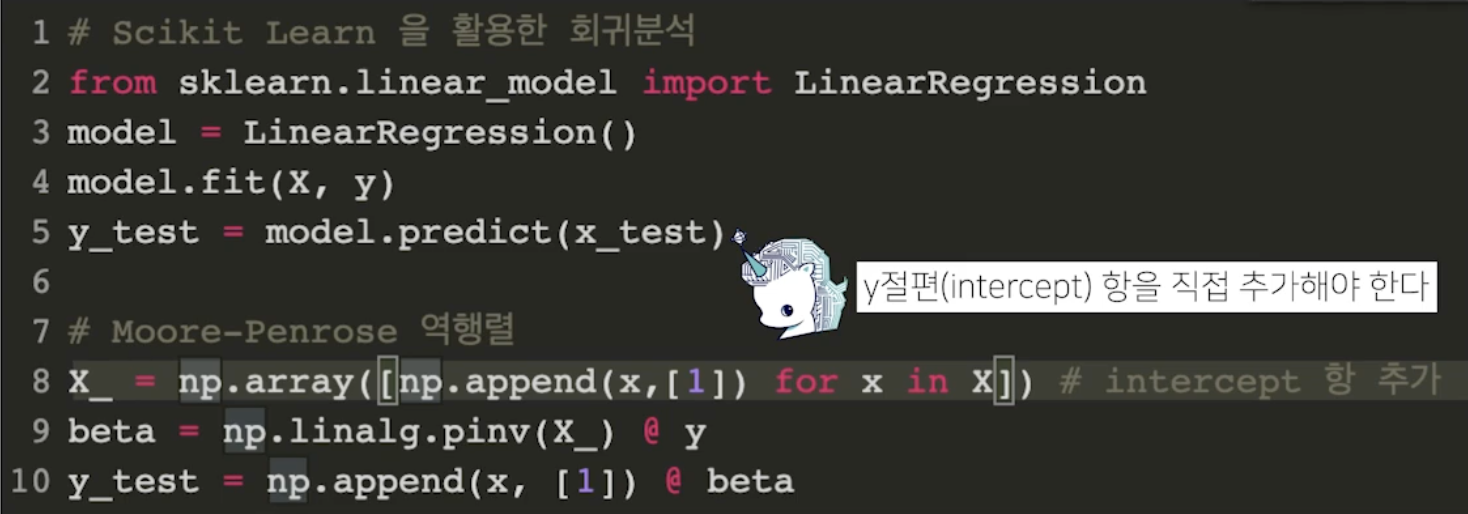
선형회귀분석
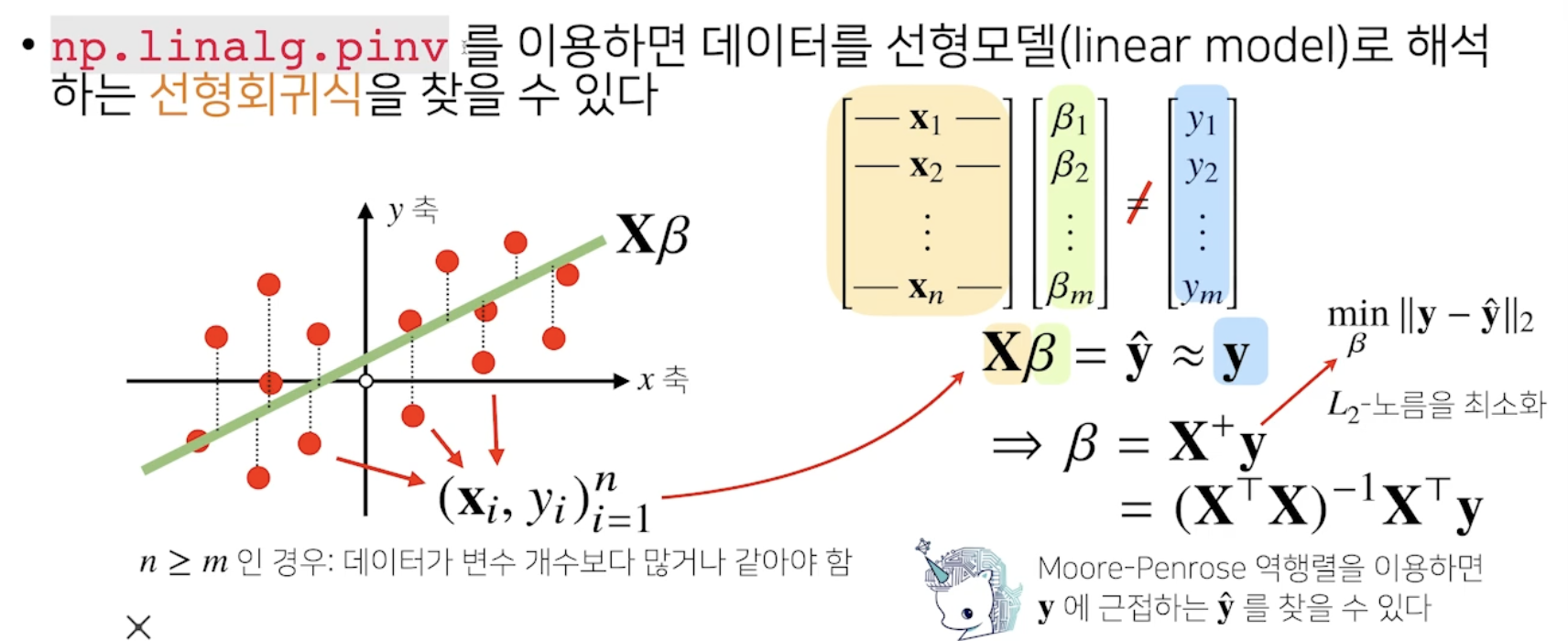
-
y절편 항을 추가해줘야 한다.