matplotlib 심화
pycharm에서 anaconda 가상환경 연결
-current file로 저장하고 run해야 작동함
-Numpy 활성화 안되는 이유는 아래에서 numpy 아직 안써서!
-cf) Set, get : 객체마다 메소드 출력해보면 set 또는 get이 나옴. Set은 설정값 넣어주는거, get은 설정값들을 불러오는거.
object=data+기능(method)
-------------------------------------매우 중요!
그래프 구성요소 용어정리
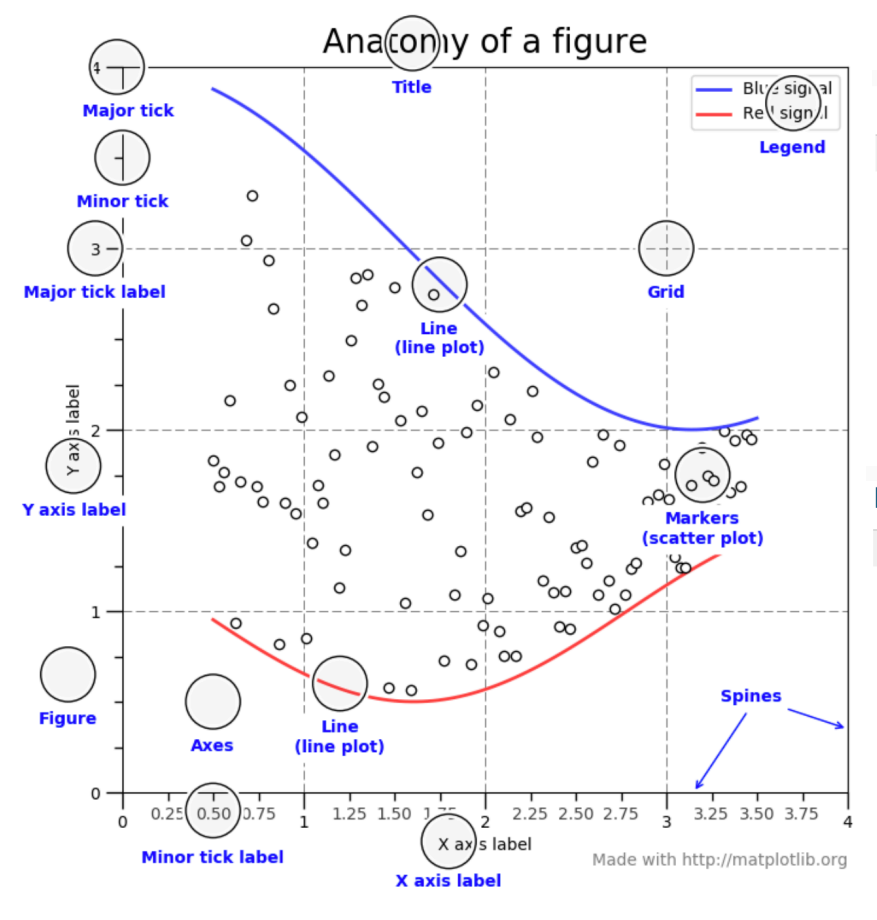
기본 그래프 설정
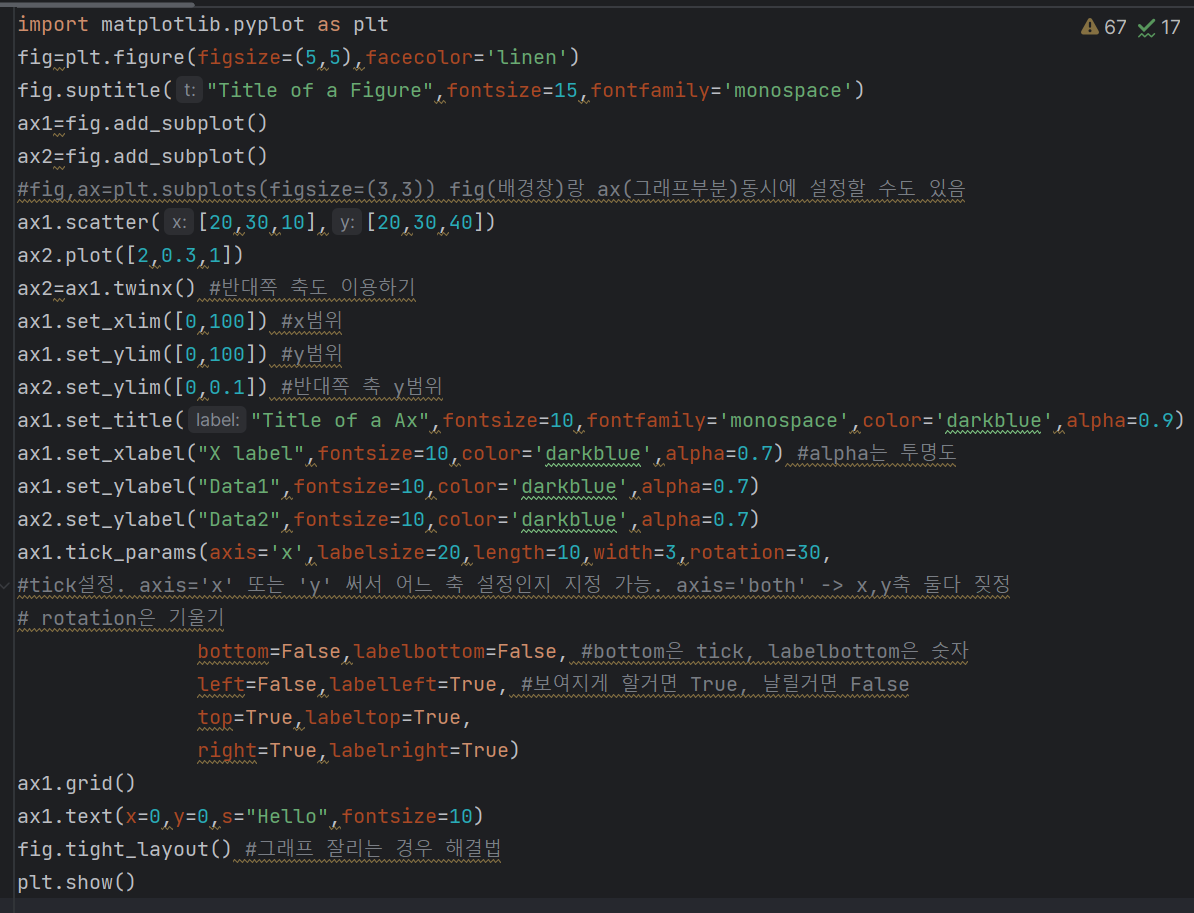
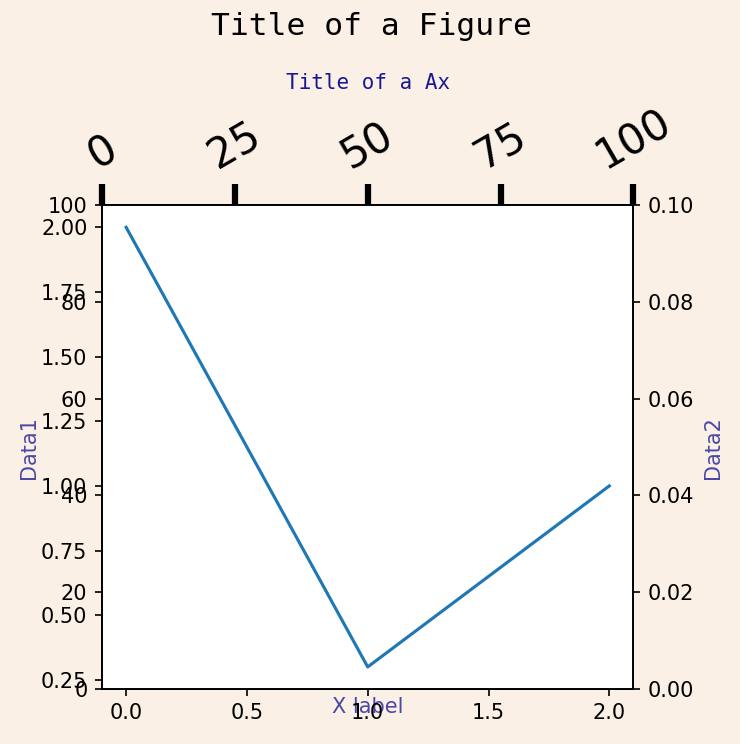
- making figures
fig=plt.figure() - fig(배경창)랑 ax(그래프부분)동시에 설정
fig,ax=plt.subplots(figsize=(3,3)) - 반대쪽 축도 이용하기
ax2=ax1.twinx() - 기본 꾸미기 설정
fontsize=10,fontfamily(글씨체)='monospace',color='darkblue',alpha(투명도)=0.9 - tick설정
-axis='x' 또는 'y' 써서 어느 축 설정인지 지정 가능.
-axis='both' -> x,y축 둘다 지정
-bottom은 tick, labelbottom은 숫자
x1.tick_params(axis='x',labelsize=20,length=10,width=3,rotation(기울기)=30,
bottom(tick)=False,labelbottom(tick에 달린 숫자)=False,left=False,labelleft=True,
top=True,labeltop=True,right=True,labelright=True)
#True면 표시, False면 날림- 그리드 설정
ax1.grid() - ax에 좌표 설정해서 텍스트 넣기(text alignment)
ax1.text(x=0,y=0,s="Hello",fontsize=10) - 그래프 잘리는 경우 해결법
fig.tight_layout() - 무조건 마지막에 plt.show()해야 그래프 뜸
text alignment(ha,va) 심화설정
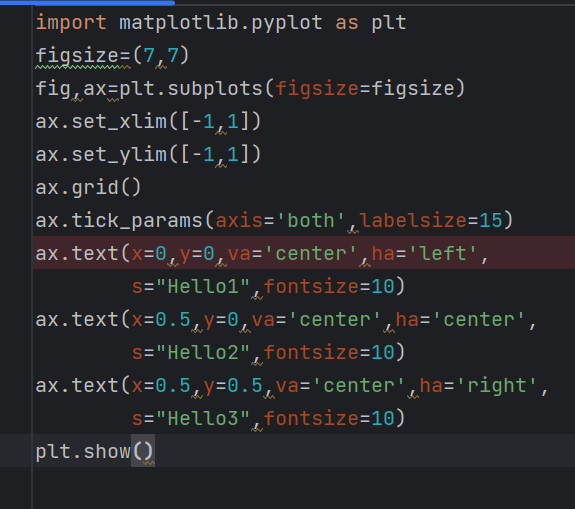
- ha(horizontal alignment), va(vertical alignment)
-top, bottom, left, right 중 설정
tick 심화 설정

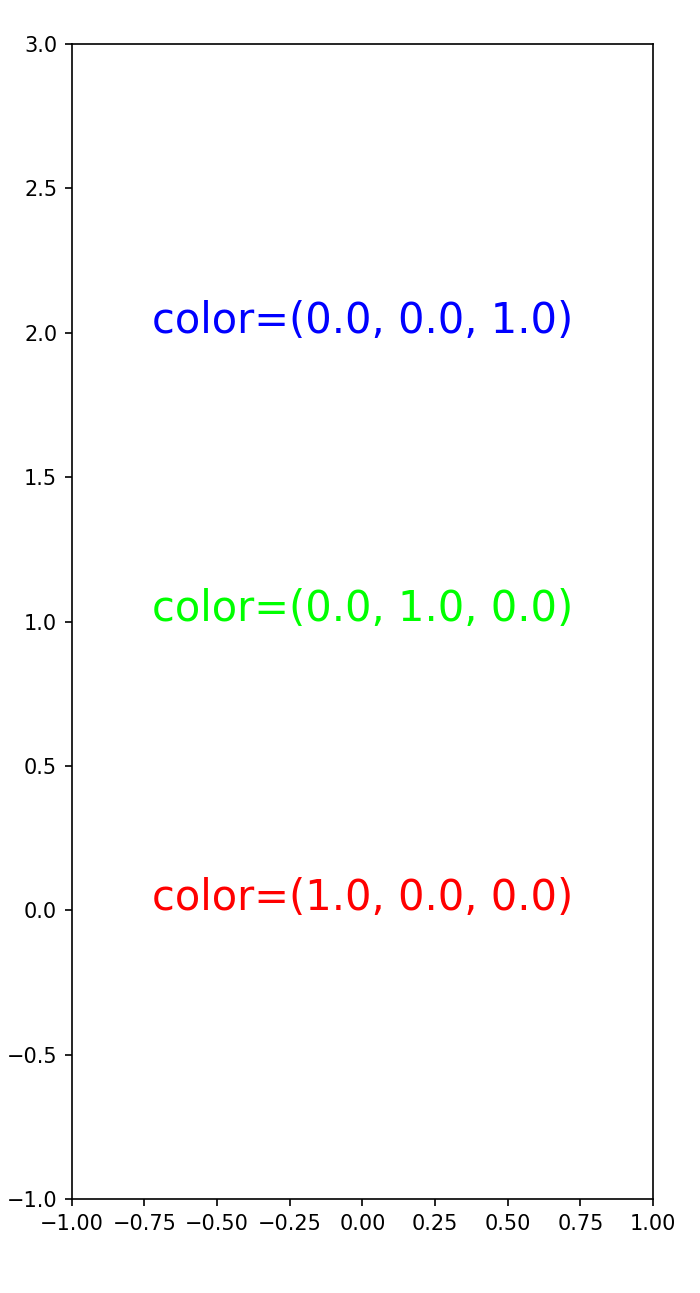
RGB 색 설정
점 그래프
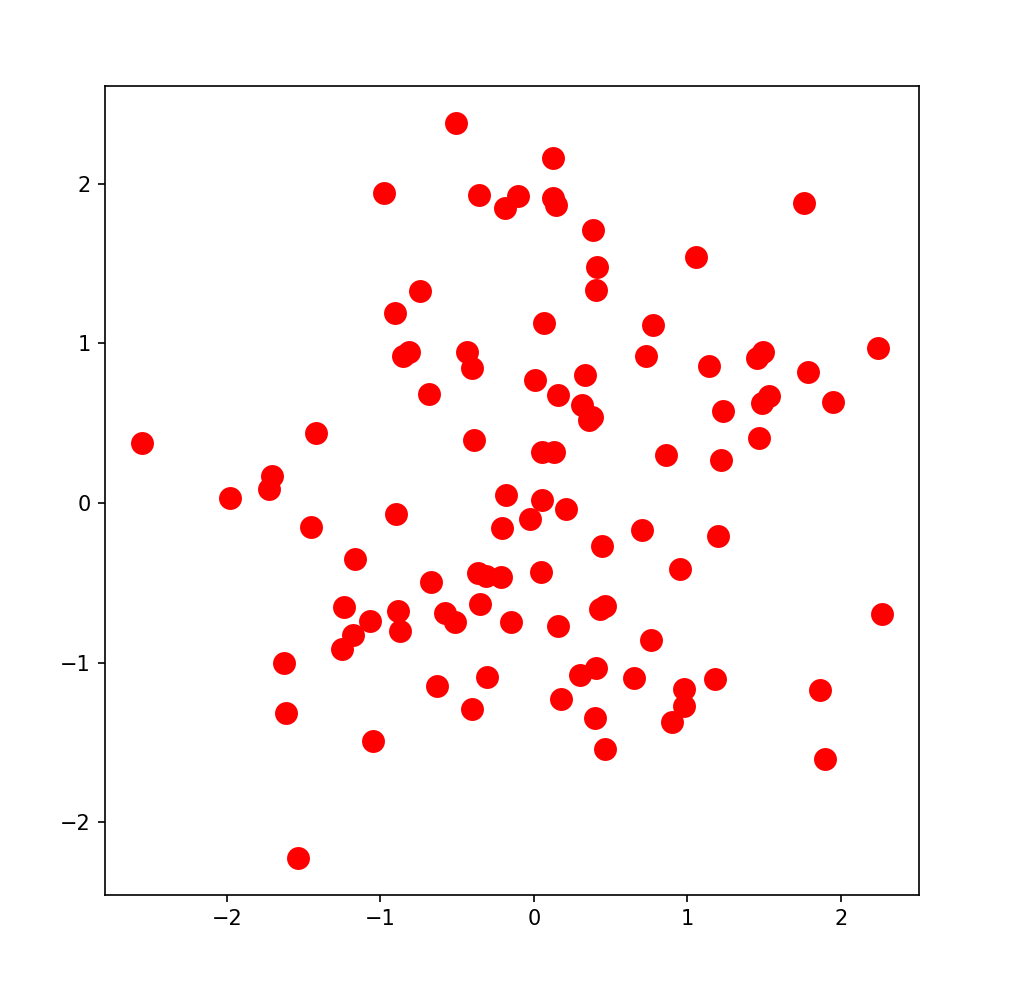
- np.random.seed : 난수 생성에 필요한 시드를 설정. 코드를 실행할 때마다 동일한 난수가 생성됨. 고정시켜주는 역할
- np.random.normal : 정규 분포 (Normal distribution)로부터 샘플링된 난수를 반환
-ex) a = np.random.normal(0, 1, 2) : 어레이 a는 정규 분포 N(0,1)로부터 얻은 임의의 숫자 2개를 반환함
추세선
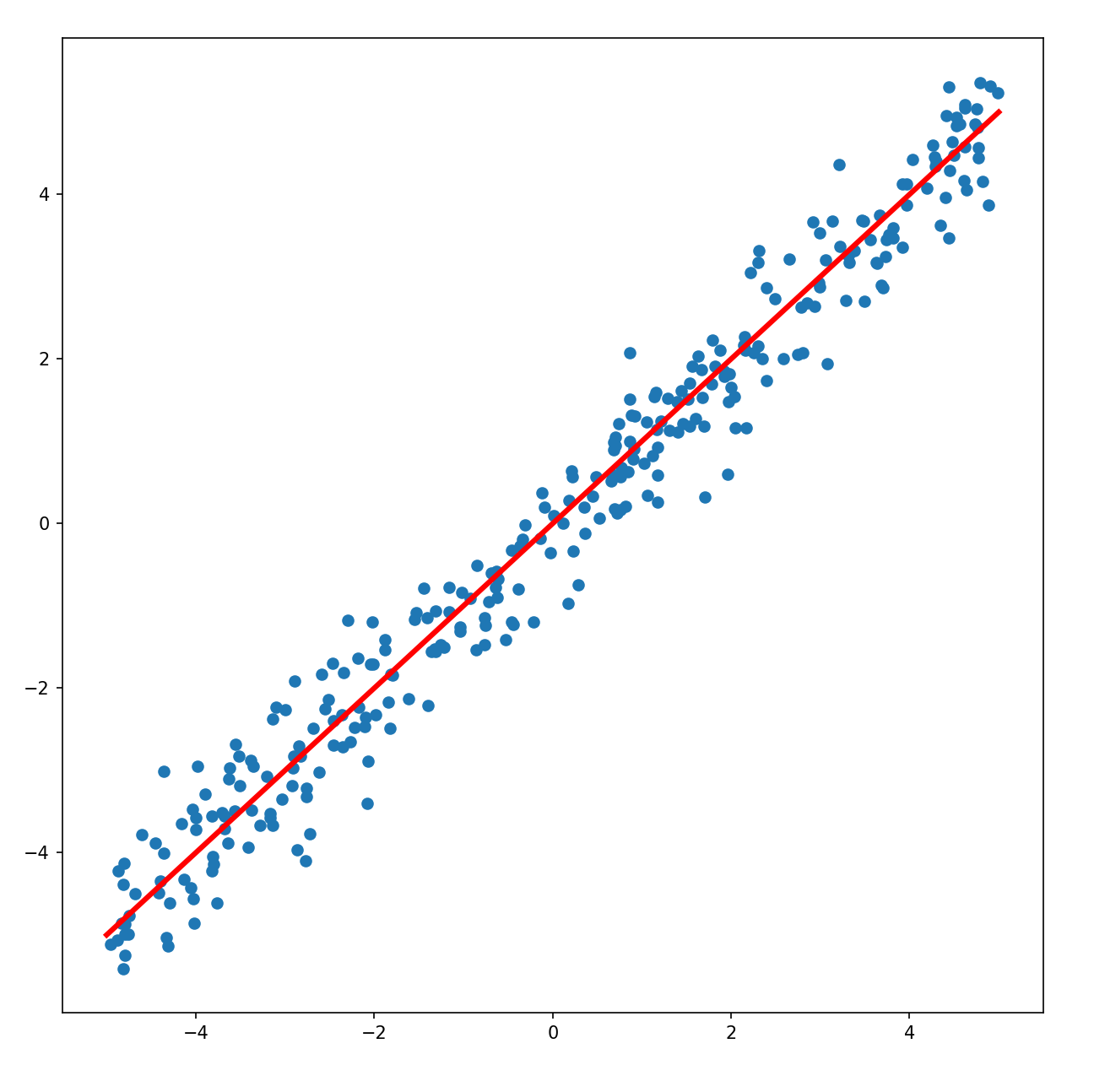
- np.random.uniform(x_min,x_max,n_data) : 균등분포함수. 최소값, 최대값, 데이터 개수 순서로 Parameter를 입력해준다(<->np.random.normal은 정규분포함수)
- np.linspace(start,stop,num) : start~stop 범위 내에서 간격 일정하게 숫자 세우기
size array, color array
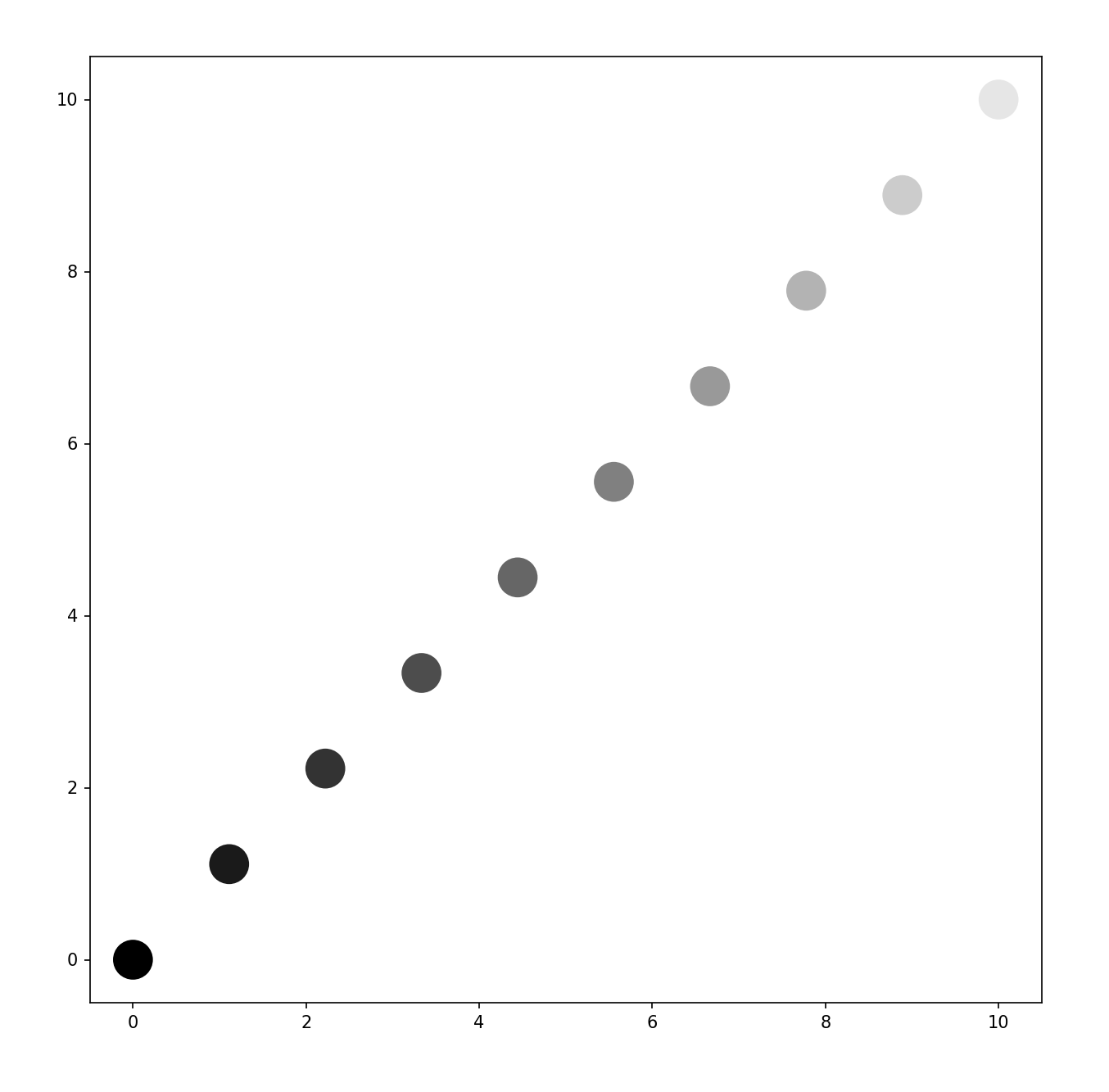
-RGB값 각각 부여
c_arr=[(c/n_data,c/n_data,c/n_data)for c in range(n_data)]
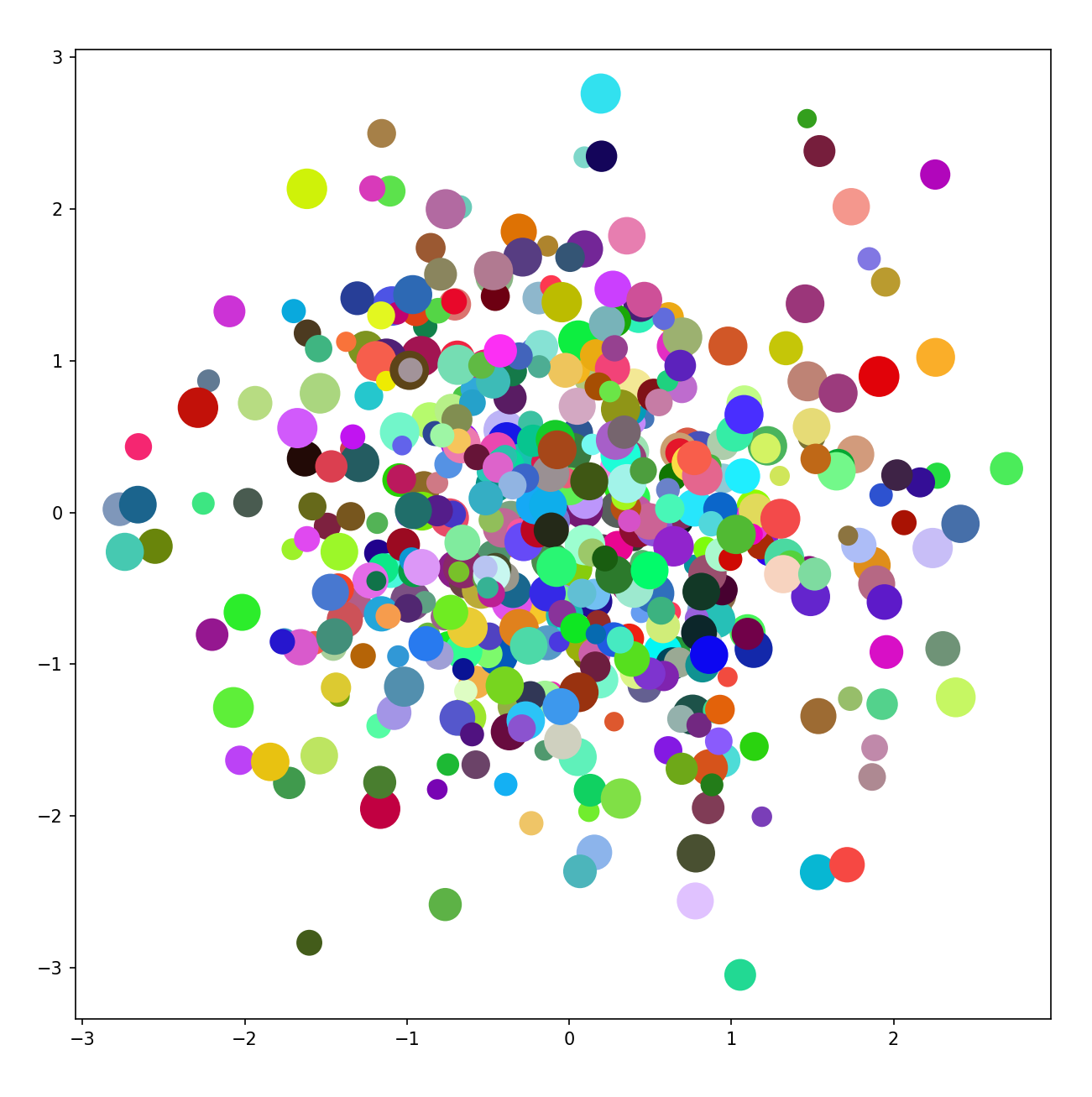
파이썬100문
mean subtraction
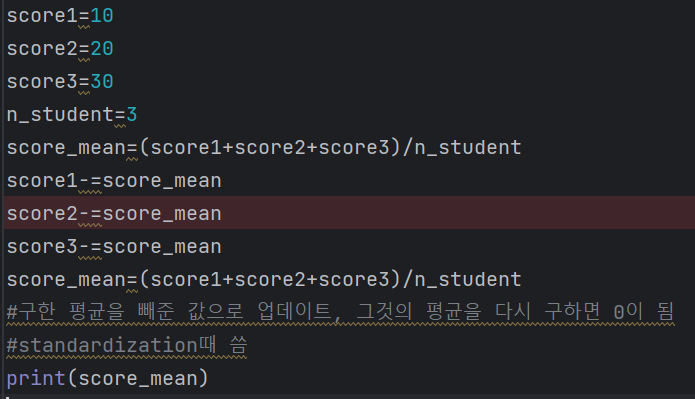 -> 0 반환
-> 0 반환
분산, 표준편차, 정규화(normalization), 표준화(standardization)
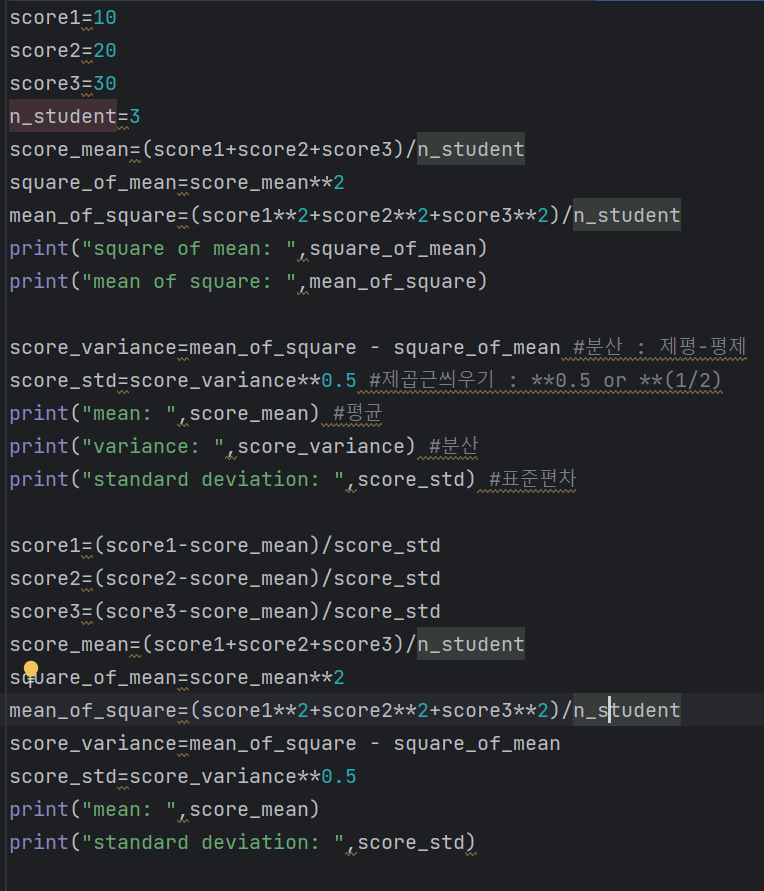
-
편차(deviation) : 평균과 데이터 값들의 차이(데이터값-평균)
-
분산 : 제곱의평균-평균의제곱
-
표준편차 : 분산의 제곱근
-표준편차 사용의 문제점
1. 표준편차는 각 데이터 간 떨어진 간격 크기를 의미하는 것이 아닌, 평균으로부터 퍼진 정도를 의미함.
2. 같은 척도를 가진데이터에서 분산, 표준편차의 크기는 의미가 있지만 다른 데이터 사이에서 분산과 표준편차의 비교는 의미x
↓
-정규화(Normalization) : 공통 간격으로 데이터 자체를 늘이거나 줄이는 방법
-표준화(Standardization) : 공통 척도로 데이터 자체를 다시 줄세우는 방법 -
표준화(Standardization) : x에서 평균 빼고 표편으로 나눠주기
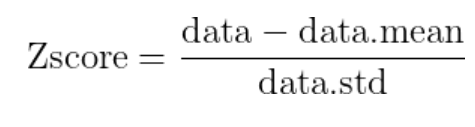 =
=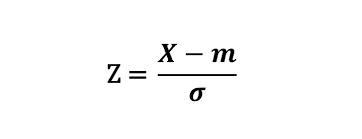
-> 평균이 0, 표준편차가 1인 공통 척도가 만들어짐. 이로써 데이터 간격의 크기는 달라질 수 있어도 데이터 간격의 의미는 달라지지 않음.
-정규분포를 표준정규분포로 만드는 것임.
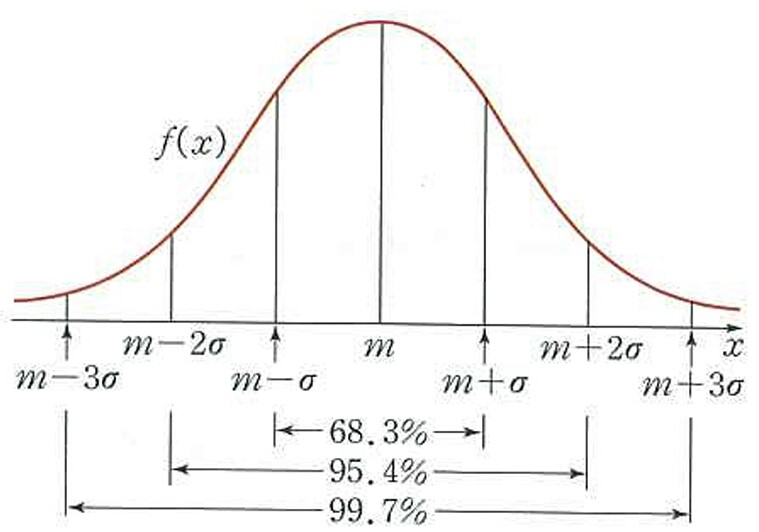 정규분포표
정규분포표
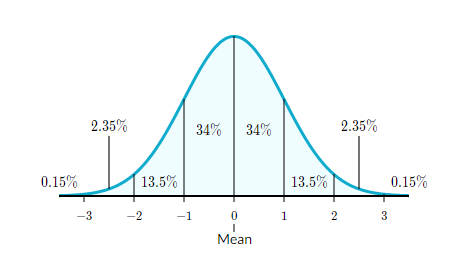 표준정규분포표
표준정규분포표
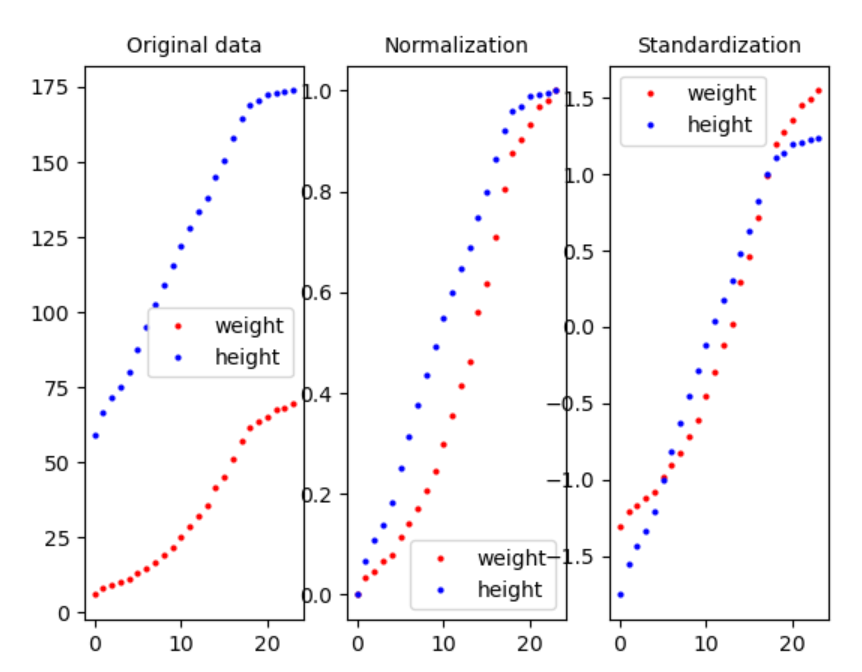 출처
출처