구간추정 대표본
즉, 알려져 있지 않은 모집단의 특성을 나타내는 모수를 theta라고 하겠습니다.
이 theta에 대한 추정을 위해 n개의 표본을 추출하였고, 이에 대한 점 추정치는 표본들의 함수라고 했습니다.
그렇다면 우리가 모르는 모수 theta에 대한 구간을 구하는데, 이 구간을 수학적으로 좀 더 엄밀히 얘기하면 100(1-a)% 신뢰구간이라는 표현을 씁니다.
여기서 a는 0과 1사이의 주어진 값이고 1-a를 신뢰수준이라고 합니다.
만약 a가 0.1 이면 모수 theta에 대한 90%신뢰구간이 됩니다.
신뢰구간은 ( L(theta hat), U(theta hat) )의 형태를 가지는데 여기서 L(theta hat) 은 theta hat의 함수이며 구간의 하한 값을 나타내고 L은 하한 값 lower bound라는 뜻에서 L을 사용했습니다.
그 다음 오른쪽에 있는 U(theta hat)은 상한 값 upper bound를 나타냅니다.
즉 모수 theta가 점 추정치로 구성된 함수인 하한 값과 상한 값 사이에 있을 확률이 1-a가 되는 구간을 모수 theta에 대한 100(1-a)% 신뢰구간이라고 합니다.

1-a라는 것은 신뢰수준 level of confidence라고 하고, 흔히 이 a는 0.01, 0.05, 0.1 등의 값을 가지게 됩니다.
그래서 만약 a가 0.01이면 99% 신뢰구간, 0.05면 95%, 0.1 이면 90% 신뢰구간 이 3가지 신뢰구간을 많이 사용하게 됩니다.

*특정 모수에 대해 신뢰구간 구하기
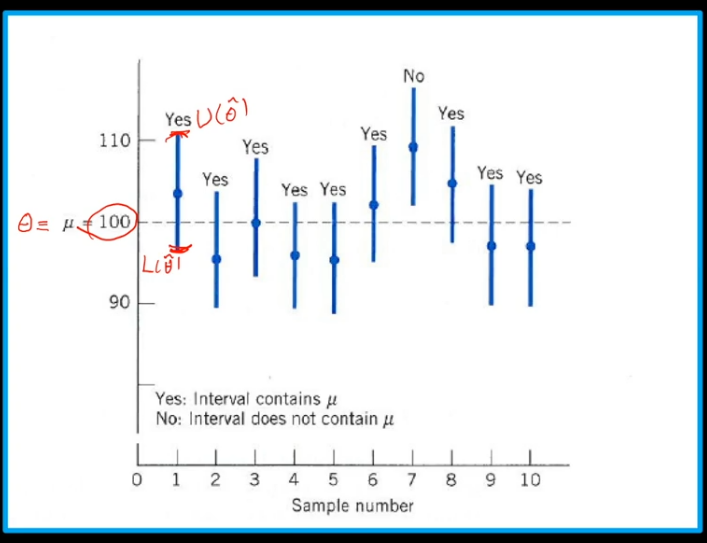
100% 신뢰구간이라는 것은 어떤 신뢰구간을 구하더라도 항상 참값인 모수 mu를 포함하는 것 입니다.
그렇게 되면 이론상으로 100% 신뢰구간은 -무한대에서 무한대밖에 없습니다.
평균이 mu이고 분산이 sigma^2인 모집단으로부터 표본을 추출할 때, 표본의 크기가 25보다 큰 대표본이라고 가정하겠습니다.

대표본은 앞에서도 소개했던 중심극한정리에서 “n이 25보다 크면 표본평균의 분포가 정규분포에 가까이 간다”에서도 이미 소개되었습니다.
일반적으로 n이 25보다 크면 대표본이라 할 수 있습니다
.
여기서 가정한 것은 모집단이 평균이 mu고 분산이 sigma^2이라는 가정만 있고 어떤 특정한 분포를 가정한 것은 아닙니다.
단지 n이 25보다 큰 대표본의 가정만 하였습니다.
이제 중심극한정리에 의해 표본평균에 모평균을 빼고 모표준편차를 나누어주면 N(0,1)에 가까이 가게 됩니다.
이제 N(0,1) pdf에서 오른쪽 꼬리 끝 면적이 a/2인 지점의 값을 z_a/2라고 표현하고, 왼쪽 꼬리 끝의 면적이 a/2가 되는 지점의 값은 정규분포는 0에 대해 대칭이기 때문에 -z_a/2가 될 것입니다.
그래서 이 통계량이 표준정규분포에 가까이 가기 때문에, 이 통계량이 이 구간에 속할 확률은 왼쪽과 오른쪽에서 a/2씩 때어내서 1-a가 될 것입니다.
즉, 이 통계량이 -z_a/2와 z_a/2 사이에 속할 확률이 1-a에 가까워지며, 이 식을 mu에 대해서 다시 정리하면 mu는 이 값들 사이에 있게 될 확률이 1-a가 됩니다.
왜냐하면 중심극한정리에서 정확하게 표준정규분포를 따르는 것이 아니라 근사적으로 표준정규분포를 따르기 때문입니다.

만약에 모 표준편차를 안다고 하면 앞에서 구한 L과 U를 신뢰구간으로 사용합니다.
만약에 모 표준편차를 모르는 경우에는 모 표준편차 대신에 표본표준편차를 대입하면 됩니다.
*구간측정
먼저 모수 theta에 대한 점 추정치를 theta hat이라 하면 모수 theta에 대한 100(1-a)% 근사적 신뢰구간은 점 추정치에서 z_a/2 s.e(theta hat)을 더하고 빼준 형태가 됩니다.
이 법칙은 표본평균뿐만 아니라 다른 모수에 대한 신뢰구간을 구할 때도 적용할 수 있습니다.
물론 z_a/2 대신 다른 상수 값이 오기도 합니다.
하지만 이 상수 값을 일반적으로 k라고 두면 신뢰구간의 일반적인 형태는 점 추정치에 k s.e(theta hat)을 더하고 뺀 형태로 쓰여 집니다.
모수가 성공의 확률 p인 베르누이 시행

Xi들이 성공의 확률 p인 베르누이 시행이므로 이것을 정규근사화 하려면 np>15, n(1-p)>15 인 조건이 필요합니다.
지금은 대 표본이고 p가 굉장히 0에 가깝거나 1에 가까운 경우가 아닐 경우로 가정하겠습니다.
iid인 베르누이 시행을 전부 더하면 이항분포가 되며 이를 X라고 하겠습니다.
이항분포의 정규 근사화

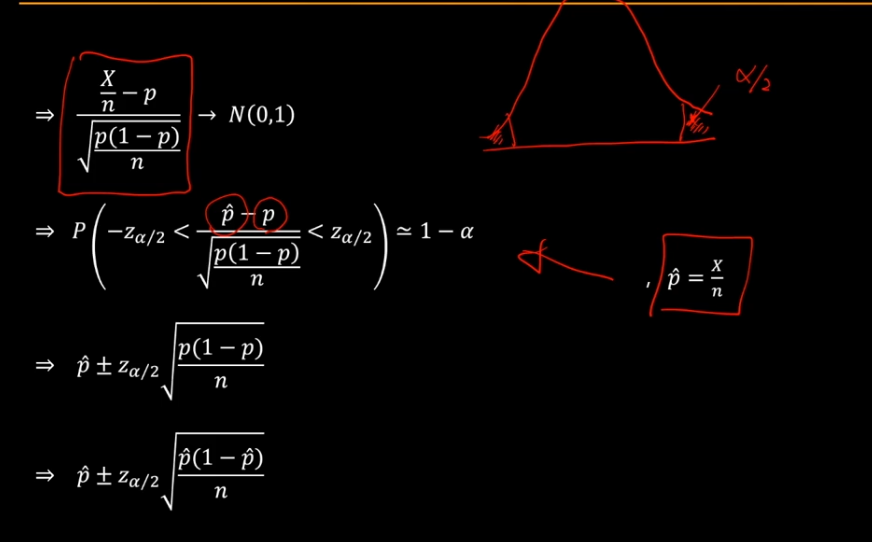
이 사실에 근거해서 표준화된 값의 분자 분모에 n을 나누어 주면 다음과 같은 값이 됩니다.
따라서 이 값이 표준정규분포에 가까이 갑니다.
여기서 phat을 X/n이라고 하면 다음과 같이되고 이 값이 표준정규분포에 가까이 가기 때문에 앞에서 한 것과 똑같은 원리로 오른쪽과 왼쪽에서 a/2씩 떼어내 가운데 면적이 1-a가 됩니다.
이것을 p에 대해서 정리하면 상한 값과 하한 값이 다음과 같이 주어집니다.
그런데 문제는 여전히 우리가 모르는 모수 p가 여전히 포함 되어있기에 이를 추정치로 바꾸어 줍니다.
이것이 바로 p에 대한 100(1-a)% 신뢰구간이 됩니다.
제가 조금 전에 말씀드린 p에 대한 100(1-a)% 근사적 신뢰구간은 역시 phat에 Za/2*s.e(phat)을 더하고 빼준 형태로 표현됩니다.
