플로이드 워셜 알고리즘

플로이드 워셜 알고리즘이란?

다익스트라 알고리즘과 비슷하게 최단 경로를 알려주는 알고리즘이란 측면에서 같지만 차이점이 있다면 다익스트라는 한 지점에서 다른 특정 지점까지의 최단 경로를 구하지만 플로이드 워셜 알고리즘은 모든 지점에서 다른 모든 지점까지의 최단 경로를 구해준다.

• '모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 하는 경우'에 사용할 수 있는 알고리즘

• 다익스트라는 1차원 리스트에 저장하지만 플로이드 워셜은 2차원 리스트에 저장(모든 노드에 대해서 최단 거리를 저장하기 때문)

• 다익스트라는 그리디 알고리즘에 속하지만 플로이드 워셜은 다이나믹 프로그래밍에 속한다.

플로이드 워셜 점화식

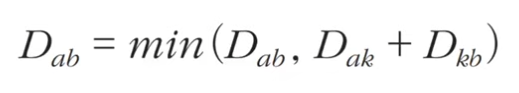
플로이드 워셜 동작과정

1. 최단 거리 테이블을 초기화한다.

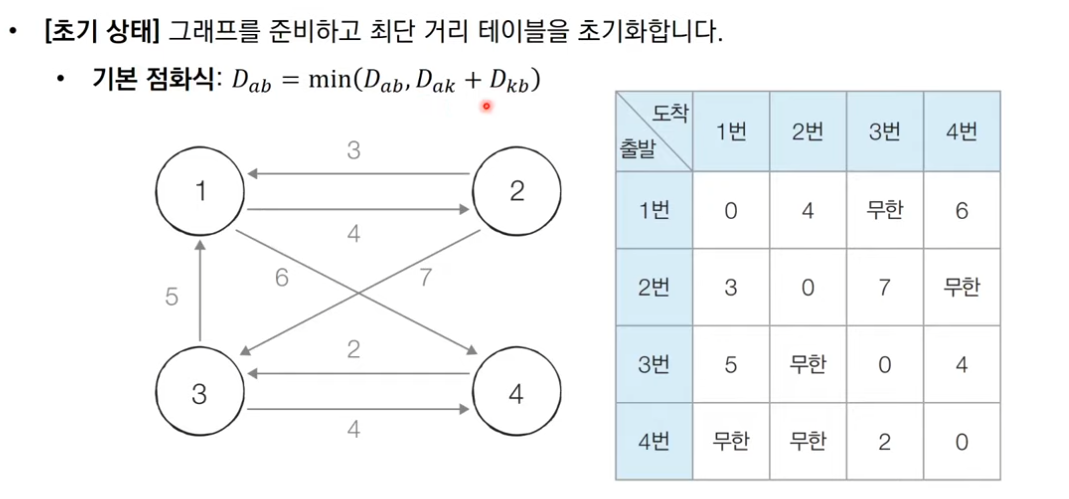
자기자신에서 자기자신으로 가는 경우(a == b)일 때 0으로 초기화하고 그래프에서 보이는 노드에 맞게 값을 초기화해준다.

2. 1번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

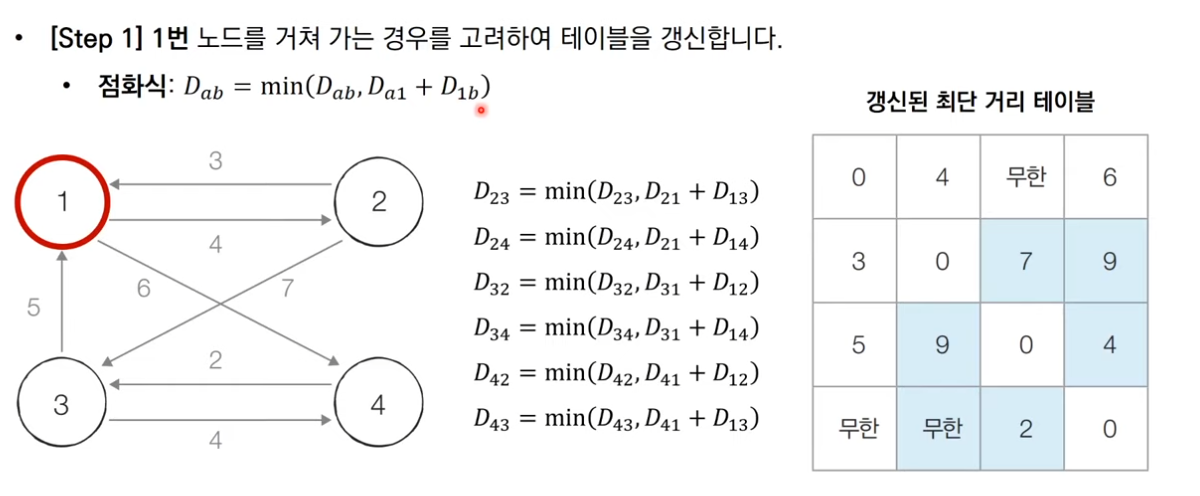
1번 노드를 거쳐간다면 변화하는 것은 1이 포함되지 않는 2, 3, 4 조합 중에 있을 것이다.

3. 2번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

4. 3번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

5. 4번 노드를 거쳐 가는 경우를 고려하여 테이블을 갱신한다.

플로이드 워셜 코드

INF = int(1e9)

print("노드의 개수 입력")
n = int(input())
print("간선의 개수 입력")
m = int(input())

#2차원 리스트(그래프 표현)을 만들고, 무한으로 초기화
graph = [[INF] * (n+1) for _ in range(n + 1)]

for a in range(1, n + 1):
    for b in range(1, n + 1):
        if a == b:
            graph[a][b] = 0

for _ in range(m):
    a, b, c = map(int, input().split())
    graph[a][b] = c

for k in range(1, n + 1):
    for a in range(1, n + 1):
        for b in range(1, n + 1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])


for a in range(1, n + 1):
    for b in range(1, n + 1):
        if graph[a][b] == INF:
            print("INF" , end= " ")
        else:
            print(graph[a][b], end = " ")
    print()