파이프 옮기기 1

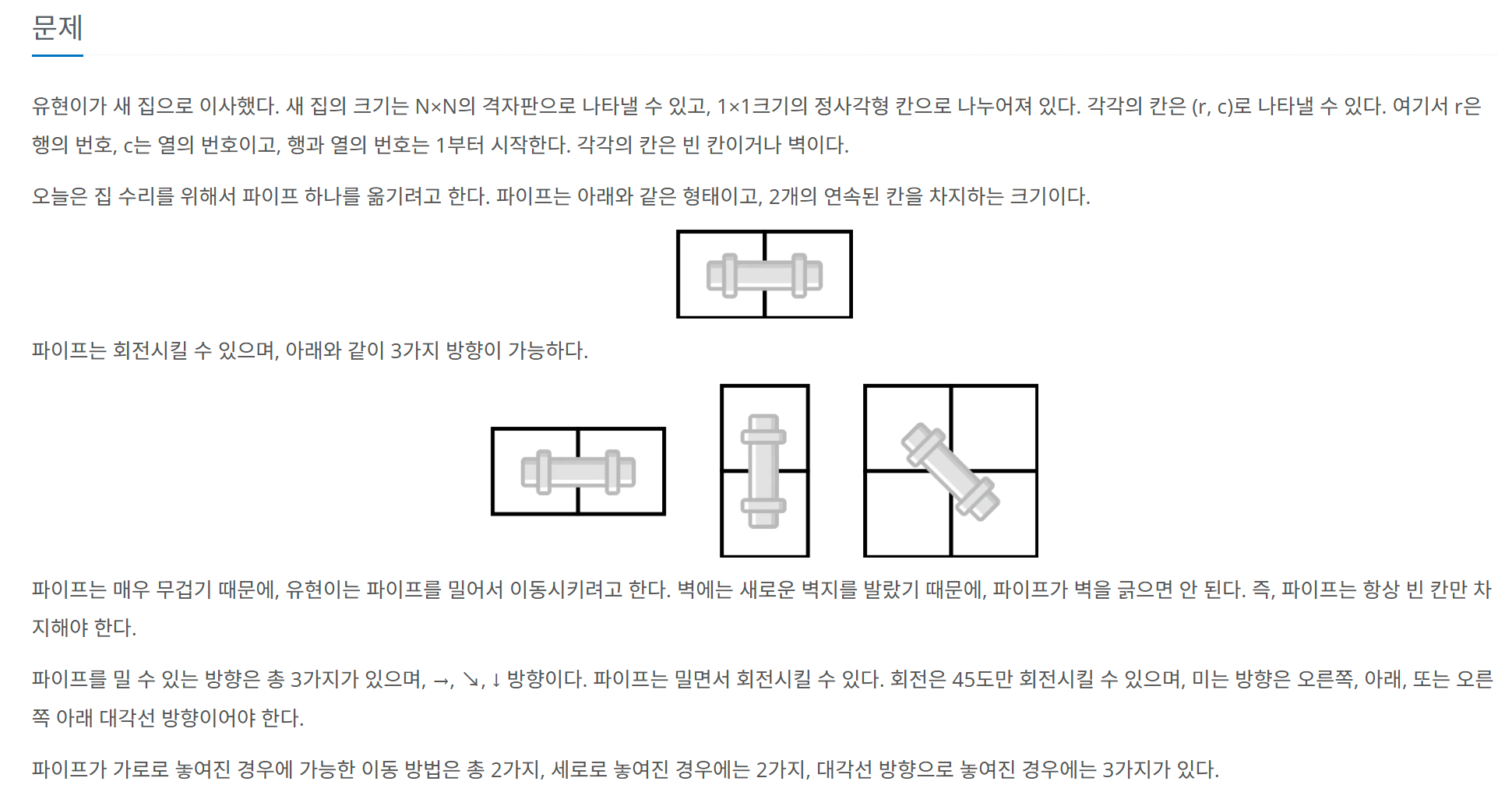
문제

풀이

처음엔 bfs로 모든 경로를 탐색했다.
하지만 시간 초과가 발생하였다.
Top - down DP로 변경하여 문제를 풀었다.

import sys
sys.setrecursionlimit(10**6)

for test_case in range(1):
    n = int(sys.stdin.readline())
    graph = [list(map(int, sys.stdin.readline().split())) for _ in range(n)]

    #방향 0 => 오른쪽 1 => 아래쪽, 2=> 대각선

    direction = [[0, 2], [1, 2], [0, 1, 2]]
    move = [[0, 1], [1, 0], [1, 1]]
    blank = [[(0, 1)], [(1, 0)], [(0, 1), (1, 0), (1, 1)]]
    dp = {}
    def dfs(cur_row, cur_col, cur_direct):
        if (cur_row, cur_col, cur_direct) in dp:
            return dp[(cur_row, cur_col, cur_direct)]
        if cur_row == n - 1 and cur_col == n-1:
            return 1
        ans = 0
        for new_direct in direction[cur_direct]:
            new_row, new_col = cur_row + move[new_direct][0], cur_col + move[new_direct][1]

            flg = True
            for r, c in blank[new_direct]:
                check_row, check_col = cur_row + r, cur_col + c

                if 0 <= check_row < n and 0 <= check_col < n and graph[check_row][check_col] == 0:
                    continue
                flg = False
                break

            if flg:
                ans += dfs(new_row, new_col, new_direct)

        dp[(cur_row, cur_col, cur_direct)] = ans
        return ans


    print(dfs(0, 1, 0))

바텀업

아이디어는 다음과 같다.
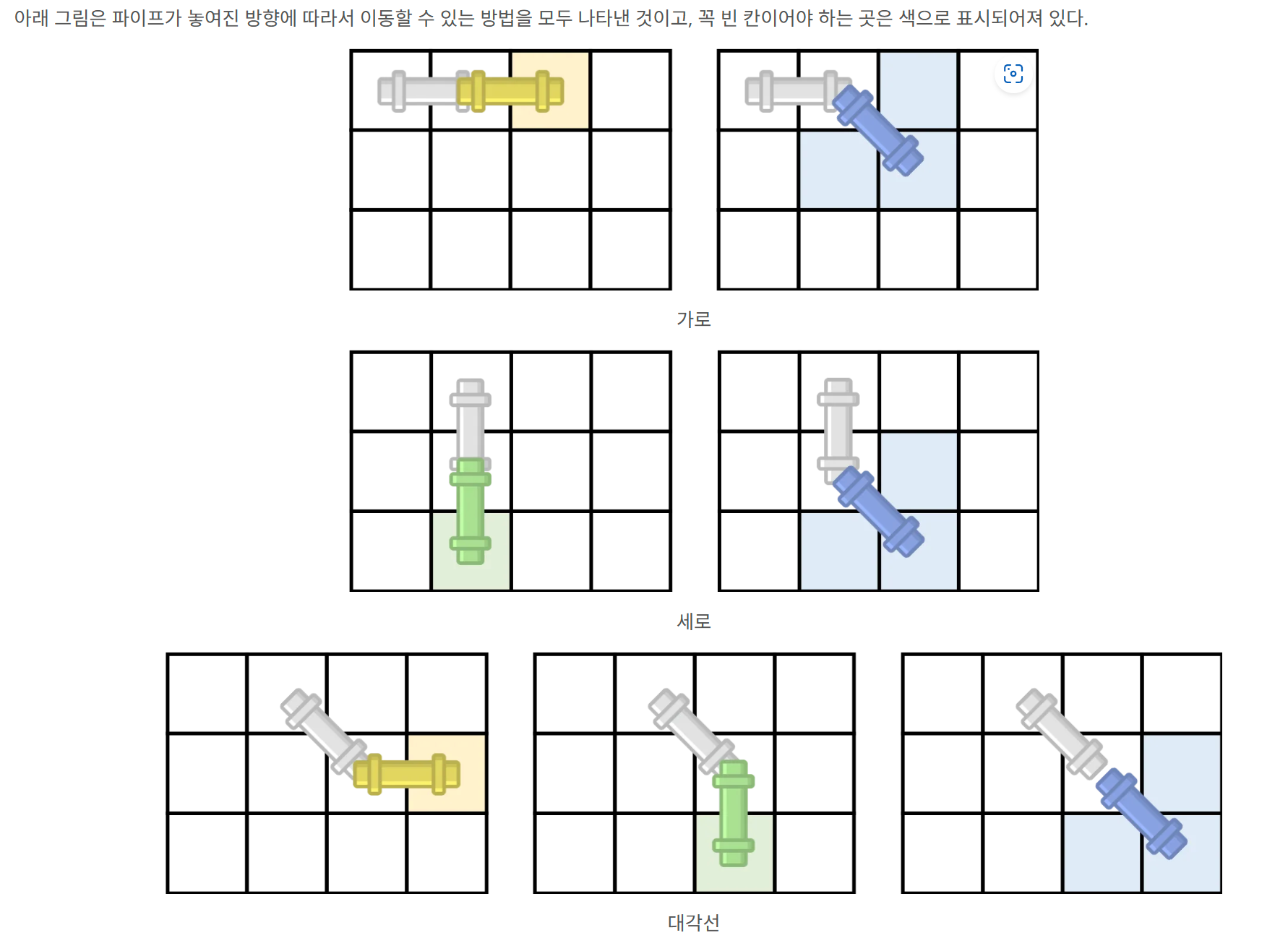
가로일 때를 생각해보자
가로가 나올 수 있는 방향은 가로, 대각선 2개이다.

세로일 때는 세로, 대각선 2개이다.

대각선일 때는 가로, 세로, 대각선 3개이다.

점화식으로 나타내보자
여기선 row,col,direct을 나타내야 하기 때문에 3차원 배열이 필요하다.
=> dp[가로][row][col] = dp[가로][row][col - 1] + dp[대각선][row][col - 1]
전 경우 세로일 경우 바로 가로가 될 수 없으므로 세로는 빼야 한다.

dp[세로][row][col] = dp[세로][row-1][col] + dp[대각선][row-1][col]
전 경우 가로일 경우 바로 세로가 될 수 없으므로 가로는 빼야 한다.

dp[대각선][row][col] = dp[가로][row-1][col - 1] + dp[세로][row-1][col - 1] + dp[대각선][row-1][col - 1]
대각선일 때에는 전에 대각선, 세로, 가로 모두 대각선 바로 갈 수 있으므로

하지만 조건이 있다.
가로, 세로는 해당 위치가 0이여야 하고
대각선은 해당위치, 위로, 왼쪽으로 0이여야 한다.

이것을 토대로 코드로 나타내면 다음과 같다.

for test_case in range(1):
    n = int(sys.stdin.readline())
    graph = [list(map(int, sys.stdin.readline().split())) for _ in range(n)]

    #방향 0 => 오른쪽 1 => 아래쪽, 2=> 대각선


    dp = [[[0 for _ in range(n)] for _ in range(n)] for i in range(3)]
    for i in range(n):
        if graph[0][i] == 0:
            dp[0][0][i] = 1

    for i in range(1, n):
        for j in range(1, n):
            if graph[i][j] == 0 and graph[i - 1][j] == 0 and graph[i][j - 1] == 0:
                dp[2][i][j] = dp[0][i - 1][j - 1] + dp[1][i - 1][j - 1] + dp[2][i - 1][j - 1]
            if graph[i][j] == 0:
                dp[0][i][j] = dp[0][i][j - 1] + dp[2][i][j - 1]  # 가로
                dp[1][i][j] = dp[1][i - 1][j] + dp[2][i - 1][j]  # 세로

    print(sum([dp[i][n - 1][n - 1] for i in range(3)]))

여기서 1열은 무조건 0이 된다.
1행은 벽이 나오는 순간 벽 뒤로는 0이 된다.
이 조건을 앞에 추가해주면 된다.

바텀업으로 생각하는 건 많이 어렵다.