트리

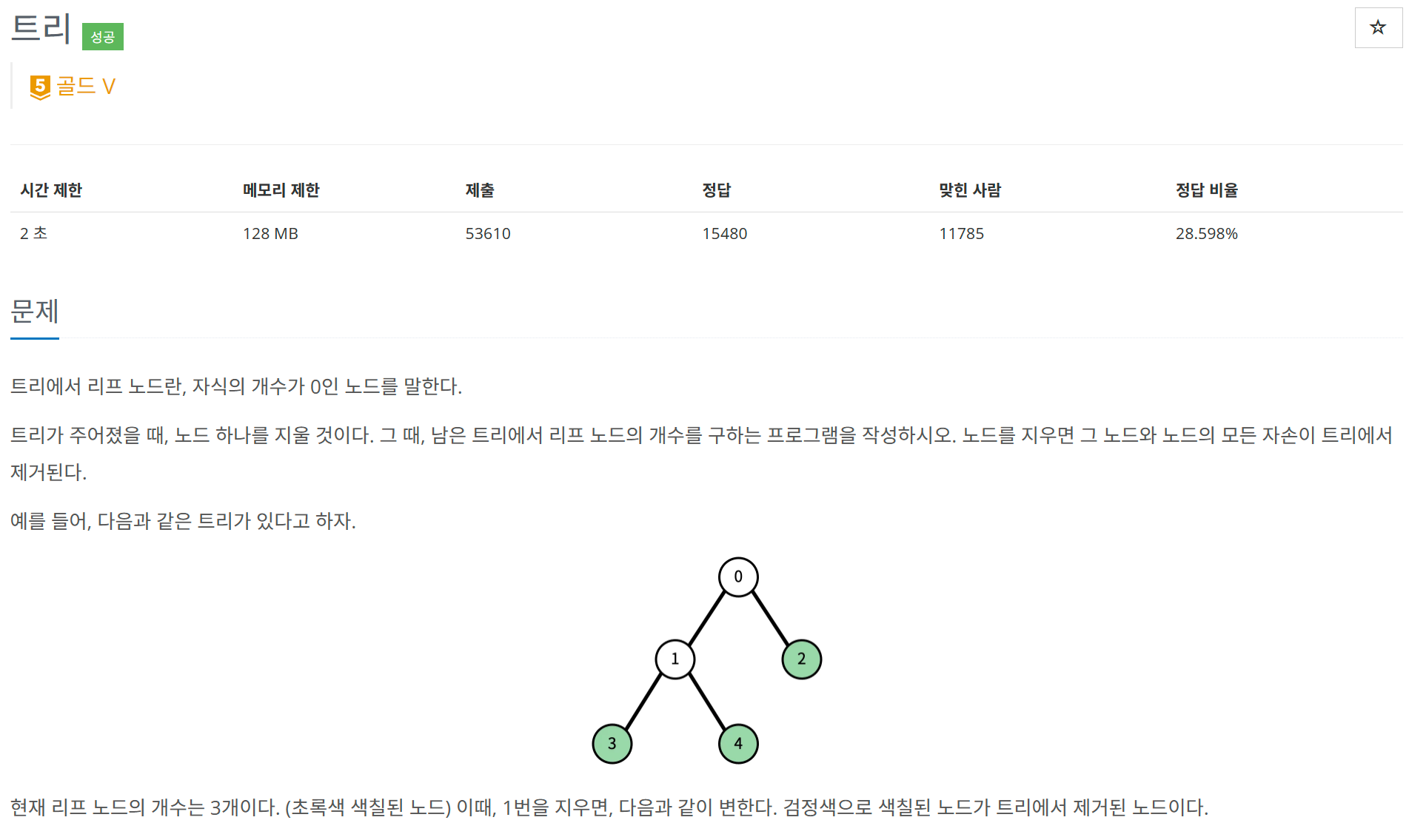
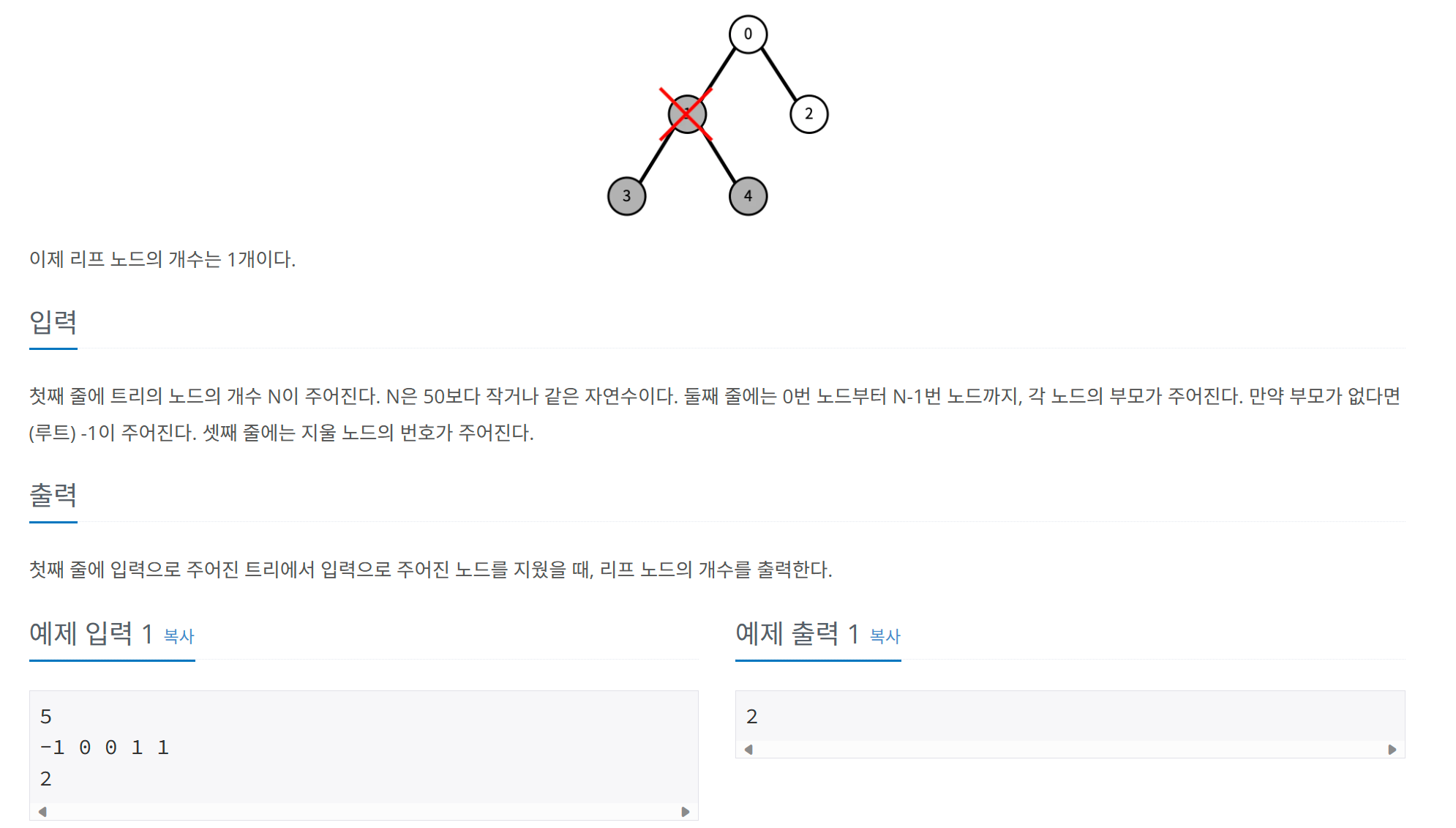
문제

풀이

앞서 내가 실수했던 부분은 이진트리만 생각해서 풀었던 것이다.
자식노드가 2 이상이 될 수 있다는 점을 고려하고 풀어야 한다.

또한 루트 노드가 항상 0번째 인덱스가 아닐 수가 있다는 것이다.
이 것을 고려하고 풀어야한다.

파이썬에서 노드를 선언해 보자
이진트리

class Node:
    def __init__(self, value, left = None, right = None):
        self.value = value
        self.left = left
        self.right = right

이진 트리일 때에는 다음과 같다. 하지만 이렇게 하면 안된다.
자식 노드가 여러개가 올 수 있다.

트리

class Node:
    def __init__(self, value):
        self.value = value
        self.child = []

    def add_child(self, child):
        self.child.append(child)

자식 노드를 배열로 두어 무한히 받을 수 있도록 하였다.

노드를 만들었으니 트리를 만드는 함수를 구현해보자
이진트리

    def makeTree(cur_node, parent, child):
        if not cur_node:
            return

        if cur_node.value == parent:
            if not cur_node.left:
                cur_node.left = Node(child)
            else:
                cur_node.right = Node(child)

        makeTree(cur_node.left, parent, child)
        makeTree(cur_node.right, parent, child)

기존에 이렇게 하여 부모노드와 자식노드간 연결을 하였다.
하지만 이렇게 하면 안된다.

트리

def makeTree(cur_node, parent, child):
        if not cur_node:
            return

        if cur_node.value == parent:
            cur_node.add_child(Node(child))

        for child_node in cur_node.child:
            makeTree(child_node, parent, child)

재귀구조를 통해 모든 트리를 탐색하고 탐색한 노드가 원하는 parent노드와 같다면 그 노드 자식에 넣어주면 된다.

삭제하는 함수를 구현해보자

이진트리

    def removeTree(cur_node, removeNode):
        if not cur_node:
            return
        if cur_node.left and cur_node.left.value == removeNode:
            cur_node.left = None
            return
        if cur_node.right and cur_node.right.value == removeNode:
            cur_node.right = None
            return
        removeTree(cur_node.left, removeNode)
        removeTree(cur_node.right, removeNode)

마찬가지로 재귀함수를 통해 모든 트리를 탐색하고 부모 노드 기준으로 자식노드를 확인해서 삭제할 노드가 있으면 해당 포인터를 None으로 바꿔준다.

트리

def removeTree(cur_node, removeNode):
        if not cur_node:
            return

        if cur_node.child:
            for node in cur_node.child:
                if node.value == removeNode:
                    cur_node.child.remove(node)
                    return

        for child_node in cur_node.child:
            removeTree(child_node, removeNode)

재귀구조로 모든 트리를 탐색하고 그 과정에서 자식 노드 배열을 확인한다.
그 중 삭제하고자 하는 노드가 있으면 삭제해주면 된다.

최종코드

import sys
sys.setrecursionlimit(10**6)
from collections import deque

class Node:
    def __init__(self, value):
        self.value = value
        self.child = []

    def add_child(self, child):
        self.child.append(child)


for test_case in range(1):
    n = int(sys.stdin.readline())
    tree = list(map(int, sys.stdin.readline().split()))
    target = int(sys.stdin.readline().rstrip())

    root = None

    def makeTree(cur_node, parent, child):
        if not cur_node:
            return

        if cur_node.value == parent:
            cur_node.add_child(Node(child))

        for child_node in cur_node.child:
            makeTree(child_node, parent, child)

    q = deque()
    for i in range(len(tree)):
        if tree[i] == -1:
            root = Node(i)
            q.append(i)
            break

        # makeTree(root, tree[i], i)

    while q:
        cur_node = q.popleft()

        for i in range(len(tree)):
            if tree[i] == cur_node:
                makeTree(root, tree[i], i)
                q.append(i)

    def removeTree(cur_node, removeNode):
        if not cur_node:
            return

        if cur_node.child:
            for node in cur_node.child:
                if node.value == removeNode:
                    cur_node.child.remove(node)
                    return

        for child_node in cur_node.child:
            removeTree(child_node, removeNode)



    def countNode(cur_node):
        global ans

        if not cur_node.child:
            ans += 1
            return
        for child_node in cur_node.child:
            countNode(child_node)


    ans = 0
    if tree[target] == -1:
        print(0)
    else:
        removeTree(root, target)
        countNode(root)
        print(ans)