LOAM

paper: LOAM: Lidar Odometry And Mapping in Real-time (or Low-drift and Real-time Lidar Odometry and Mapping)

LOAM은 논문 제목대로 Lidar Odometry And Mapping의 줄임말로 high accuracy ranging과 inertial measurement 없이 Low-drfit, Low-computational complexity를 가진 odometry라고 한다.

Odometry는 아주 복잡한 문제인 SLAM 문제의 일부이며 이 odometry를 아래처럼 두 부분으로 나누어서 해결했다고 한다.

motion estimation을 위해 높은 frequency로 돌아가지만 신뢰도가 비교적 낮은 odometry
위의 알고리즘에 비해 frequency가 낮지만 fine registration을 할 수 있는 mapping
LOAM의 전제 시스템은 다음과 같다.

1 Lidar input이 들어오면 registration을 해서 Lidar odometry를 한다.
2 Odometry의 결과 pose를 이용해 Lidar mapping을 한다.
3 Mapping의 결과와 Odometry의 pose결과를 합쳐서 finagl pose를 얻는다.

Lidar Odometry

1) Feature Point Extraction

Registration에 사용되는 feature는 edge와 plane이다. 그래서 point마다 edge point인지 planar point인지를 구별하기 위해서 smoothness를 구해서 이를 판별하였다.

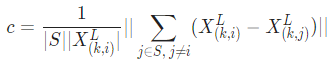
여기서S는 표현이 애매한데 내가 이해한 바로는 point i와 consecutive한 point들의 set이며 양쪽 side를 반반씩 가지고 있는 set리고 한다. LeGO-LOAM 구현코드에서는 양쪽 point 5개씩 사용한것을 봐서는 결국 양쪽에 n개씩 사용한다는 뜻인것 같다. |S|,|X|은 거리, set의 크기에 대한 normalize term역할을 한다.
그래서 이 maximum c들을 edge point 로 minimum c들을 planar point로 한다고 하는데 식을 보면 edge인 경우에 현재 point를 기준으로 consecutive한 point가 어느 한쪽으로 몰려있기 때문에 c의 값이 커지고 planar의 경우 평평할수록 현재 point를 지나는 대칭형태의 line이 되므로 값들이 상쇄되어 0에 가까워진다.
그리고 feature point를 골고루 뽑기 위해 90도씩 4개의 subregion으로 나누고 각각의 region마다 threshold를 만족하는 edge는 최대 2개, planar는 최대 4개를 찾도록 하였다.

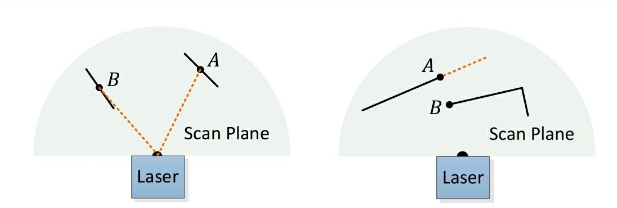
그리고 feature point를 골고루 뽑아야 하므로 주변에 feature point가 존재하면 뽑지 않도록 하였고 occluded region의 boudary또한 실제로는 planar인데 edge로 뽑힐 가능성도 있으므로 뽑지 않으며 laser beam에 parallel한 surface는 대체로 unreliable하므로 이또한 뽑지 않도록 한다. 이런 과정을 통해 edge point와 planar point는 아래와 같이 뽑힌다.
(노란색 : Edge, 빨간색 : Planar)

2) Finding Feature Point Correspondence

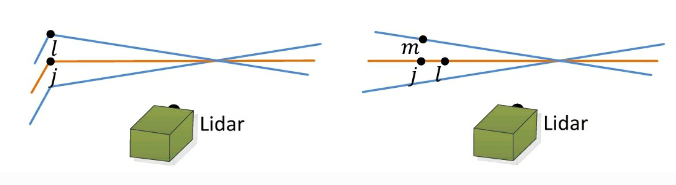
Feature를 찾았으면 registration을 위해서 서로 다른 scene의 feature들 간에 correpondence를 생성해야한다. $P_{k+1}$에서 찾은 edge와 planar를 $E_{k+1}, H_{k+1}$이라 하면 이 point들에 대해 $P_k$에 있는 point중 nearest point를 찾아 correspondece를 만든다고 한다.
edge point:
$i∈E_{k+1}$ 에 대해서 $P_k$에서의 nearest point를 $j$라고 하고 edge line을 형성하기 위해서는 2개의 point가 필요하므로 $j$의 consecutive point $l∈P_k$를 구하고 이 $j,l$에 대해 smoothness를 계산해 둘 다 edge point라면 $(j,l)$)이 이루는 edge line과 $i$ 사이에 correspondence를 만들고 다음과 같은 식으로 correspondence의 distance를 구한다.

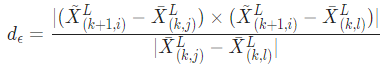
planar point: $i∈H_{k+1}$에 대해서 $P_k$에서의 nearest point를 $j$ 라고 하고 plane을 형성하기 위해서는 3개의 point가 필요하므로 세 점이 한 직선을 만들지 않도록 $j$ 의 nearest neighbor 2개의 $l,m∈P_k$ 를 구하고 이 $j,l,m$ 에 대해 smoothness를 계산해 셋 모두 planar point라면 $(j,l,m)$이 이루는 plane과 $i$ 사이에 correspondence를 만들고 다음과 같은 식으로 correspondence의 distance를 구한다.

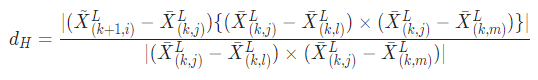
3) Motion Estimation

위에서 구한 correspondence를 이용해 두 frame사이의 motion estimation을 해야한다. 그런데 lidar point는 모든 point가 동시에 찍혀 나오는것이 아니라 일정한 속도로 sweep을 하면서 한 frame을 완성하는 것이기에 linear interpolation을 해줘야 한다. 그래서 transformation을 구한 시점 $t$ 에서의 6-DOF transformation을 $T^L_{k+1} = [t_x,t_y,t_z,θ_x,θ_y,θ_z]^T$이라고 하고 transform 하는 point의 index를 $i$ 라고 하면 point $i$ 에 한 transformation은 다음과 같다.

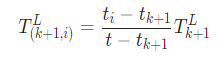
motion estimation을 위해서는 두 frame에서 찾은 feature들 사이의 transform matrix를 구해야한다. 즉 아래의 식을 만족하는 transformation을 구해야한다.

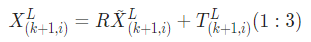
여기서 $R$ 은 optimization을 위해서 $T^L_{(k+1,i)}(4:6)$ 을 Rodrigues formula를 통해서 구한 $ω$ 의 skew symmetric matrix이다.
위의 문제를 optimization problem으로 풀기 위해 correpondence의 거리가 가까워진다는 것은 제대로 registration(motion estimation)이 이뤄졌다는 의미이므로 아래와 같이 edge correspondence와 planar correspondence를 cost로 삼는다.

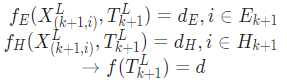
optimization에 사용된 알고리즘은 Levenberg-Marquardt이다.

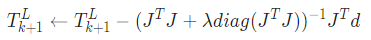
4) Lidar Odometry Algorithm

lidar odometry에 사용된 알고리즘을 정리하자면 위와 같다. 앞에 소개한 방법론들을 순차적으로 진행하여 얻은 transform을 통해 odometry를 한다.

5) Lidar Mapping

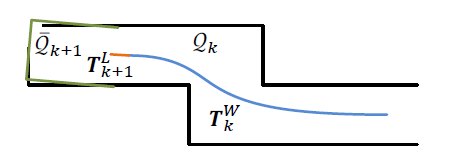
lidar mapping은 odometry보다 더 낮은 빈도로 실행되고 sweep이 완성된 후에만 실행된다. odometry에서 구한 motion으로 untwist된 point cloud $\overline{P}_{k+1}$ 을 world coordinate상의 map에 registration하는 과정이다.

$Q_k$ 를 sweep $k$ 가 끝난 시점에서의 pose주변의 cubic area내에 존재하는 map point들의 set이라 하고 $\overline{P}_{k+1}$을 mapping을 통해서 가장 최근에 얻은 transformation인 $T^W_k$으로 transform한 point를 $\overline{Q}_{k+1}$이라 하면 odometry에서 한 것처럼 feature extraction, finding correspondence, motion estimation을 통해서 $\overline{Q}_{k+1}$을 $\overline{Q}_{k}$ 에 registration을 한다.

mapping에서 $\overline{Q}_{k+1}$ 에 대한 feature extration은 이미 odomery에서 했기 때문에 그대로 사용한다. odometry가 10Hz로 돌아가고 mapping이 1Hz로 돌아가기 때문에 10배의 feature를 사용하게 된다.

correspondence 생성은 $\overline{Q}_{k+1}$의 각 feature point마다 주변에 존재하는 $Q_k$의 point의 set $S'$을 구하고 $S$ 에 대해서 matrix decomposition을 통해 eigenvalue와 eigenvector를 구하고 eigenvalue에서 dominant한 value의 갯수가 2개면 plane, 1개면 edge라고 판별하고 edge line과 planar patch의 position은 $S'$ 의 geometric center로 삼아서 feature point과 이 center사이의 corresopndence를 생성한다.

optimization은 마찬가지로 Levenberg-Marquardt를 사용해서 transformation을 구한다.

그리고 마지막으로 pose integration은 mapping이 상대적으로 fine registration이기에 이미 존재하는 mapping에 odometry pose를 쌓는방식으로 한다. 따라서 실시간으로 얻는 pose의 결과는 $T^L_{k+1}T^W_K$가 되는 것이다.

출처 : https://dreambreaker-ds.tistory.com/entry/LOAM-Lego-LOAM