페르마의 소정리

$p$가 소수이면, 모든 정수 $a$에 대해 $a^p \equiv a \; (mod \; p)$이다.
혹은, $p$가 소수이고 $a$가 $p$의 배수가 아니면, $a^{p-1} \equiv 1 \; (mod \; p)$ 이다.

이를 이용해서 이항계수를 빠르게 구할 수 있습니다.

백준 11401 이항 계수 3

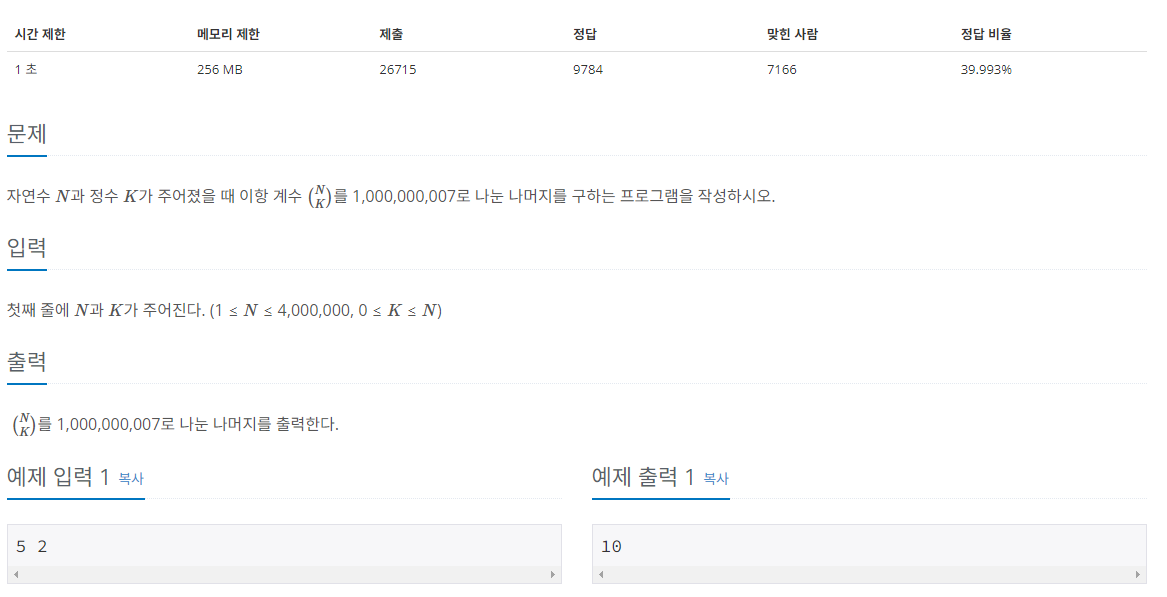
이항 계수 $\binom{N}{K}$를 변환하여 페르마의 소정리를 이용할 수 있습니다.

$\binom{N}{K} = \frac{N!}{K!(N-K)!} = N!({K!(N-K)!})^{-1}$와 같이 변환이 가능하고,
페르마의 소정리를 이용하여
$\binom{N}{K} \; \% \; p = N!({K!(N-K)!})^{p - 2} \; \% \; p$가 성립합니다. (위 문제에서, $p$는 1,000,000,007)

---

코드 (C++)

#include <bits/stdc++.h>

using namespace std;

const int P = 1000000007;

long long getFactorial(long long n)
{
	long long ret = 1;

	for (int i = 1; i <= n; i++) {
		ret = ret * i % P;
	}
	return ret;
}

long long fastMultiply(long long a, long long b)
{
	if (b == 0) return 1;
	if (b == 1) return a % P;

	long long tmp = fastMultiply(a, b / 2);

	if (b % 2 == 0) {
		return tmp * tmp % P;
	} else {
		return tmp * tmp % P * a % P;
	}
}

int main()
{
	ios_base::sync_with_stdio(false);
	cin.tie(nullptr);
	cout.tie(nullptr);

	long long N, K;
	cin >> N >> K;

	cout << getFactorial(N) * fastMultiply(getFactorial(K) % P * getFactorial(N - K) % P, P - 2) % P << "\n";
	return 0;
}