Linear Classification (1): Update rules

Overview

이진 분류를 선형분류기로 할 때, 가중치와 바이어스를 업데이트 하는 방식에 따라 학습이 어떻게 달라지는지 알아보자.

In linear classification, the weights and the bias are updated by the following equations. We analyze the learning by changing the update functions.

What is the linear claasification?

데이터 속성의 선형결합으로 데이터를 분류하는 작업 (위키백과)
Classify the data as a linear combination of the features of the data

$y^{'}$: prediction
$x$: input features
$W$: weight matrix, ($\omega_{1}$, $\omega_{2}$)
$b$: bias
$\sigma$: step function (activation function)

Update rules

선형분류에서 가중치와 바이어스는 4) 식과 같이 업데이트 된다. 각 식으로 업데이트를 했을 때 학습이 어떻게 달라지는지 알아보자.
In the linear classification, the weights and the bias are updated by the below equations. We analyze the learning through changing the update functions.

Update rule: $\omega^{'}$ = $\omega$ + $\eta d(x)$

$\eta$: 학습률 (learning rate)
$d(x)$: update function
$y$: true label
$y^{'}$: prediction

1) $d(x)$ = $(y - y^{'})$
2) $d(x)$ = $(y^{'} - y)$
3) $d(x)$ = $(y^{'} - y)x$
4) $d(x)$ = $(y^{'} - y)x$

Result

• $d(x)$ = $(y - y^{'})$ & $d(x)$ = $(y^{'} - y)$
  
  
  1번과 2번식으로 업데이트를 하게 되면 모든 가중치가 똑같은 값으로 업데이트 된다. 따라서 선형 분류기의 기울기가 변하지 않는다. 이로 인해 분류 성능이 바이어스에 의해서만 결정되기 때문에 좋지 않다.
  
  The weights and the bias are updated in the same way as if they were updated by the update functions 1) and 2). Therefore, the slope of the line is not changed and the classification performance depends only on the bias.
  
  

• $d(x)$ = $(y^{'} - y)x$
  
  
  1), 2) 식과 달리 입력 값 $x$가 곱해지기 때문에 $\omega_{1}$과 $\omega_{2}$의 업데이트 양이 달라진다. 하지만 이 식으로 학습 시, 두 데이터 집합을 구분하지 못하는 것을 알 수 있다.
  
  In the following figure, the line can't distinguish the data set.
  

• $d(x)$ = $(y - y^{'})x$
  
  
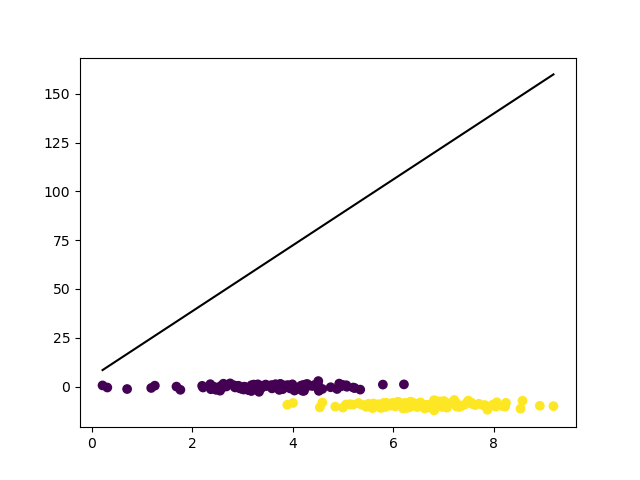
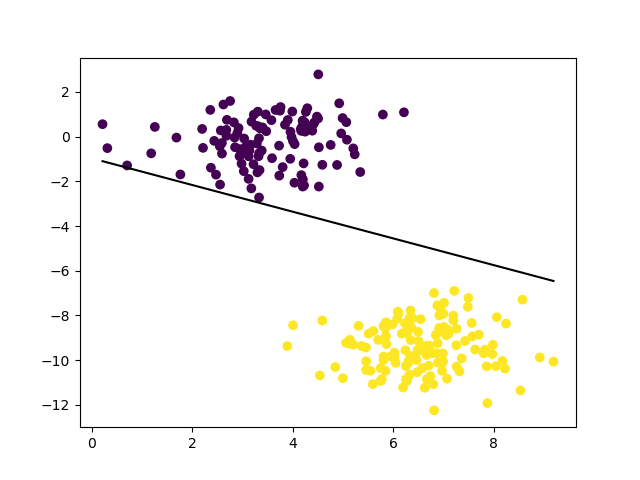
  두 데이터 집합을 구분하는 것으로부터 학습이 잘 이루어진 것을 알 수 있다.
  
  We can see from the following figure that the training has done a good job of distinguishing between the two datasets.
  

Discussion

1) 과 2)의 식으로 업데이트를 하면 $\omega_{1}$ 과 $\omega_{2}$의 값이 바뀌지만, 항상 같은 비율로 변하기 때문에 기울기가 업데이트 전과 동일하다. 이로 인해 분류 성능이 변하지 않는다. 3) 식은 업데이트에 따라 기울기가 달라지지만, 업데이트 방향이 잘못되어 오히려 안 좋아진다. 반면 4) 식은 올바른 방향으로 업데이트 시키기 때문에 분류 성능이 향상된다.

Update 식의 구성을 살펴보면 ±($y$ - $y^{'}$ )는 업데이트 방향을 결정하는 부분으로, 직선이 올라갈지 내려갈지 결정된다. 하지만 단독으로는 변화를 줄 수 없다 ($x$가 곱해져 있지 않을 때는 기울기가 업데이트 이후에도 동일하기 때문).

Updating the equations in 1) and 2) changes the values of $\omega_{1}$ and $\omega_{2}$, but because they always change at the same rate, the slope is the same as before the update. This keeps the classification performance unchanged. Equation 3) has a slope that changes with the update, but it's worse because the update is in the wrong direction. On the other hand, expression 4) improves the classification performance because it updates in the right direction.

If you look at the construction of the update expression, ±($y$ - $y^{'}$ ) is the part that determines the direction of the update, which determines whether the straight line goes up or down. However, it can't make a difference by itself (since the slope after the update is the same if $x$ is not multiplied).