다이나믹 프로그래밍

*이 글은 2022년 1월~2월 노션으로 진행한 알고리즘 스터디를 옮긴 글입니다. 나동빈 저자 이것이 취업을 위한 코딩테스트다를 사용해 학습했습니다.

220218 다이나믹 프로그래밍 개념 정리

• 필기
  

• 정리
  • 바텀업 방식이 더 빠름(재귀함수가 그냥 느린편)
  • 메모이제이션은 탑다운 방식에 국한돼있음
  • 분할정복 알고리즘(ex.퀵정렬)과 별개임. 동적계획법은 이미 해결된 문제가 또 해결되는 경우o.

---

220218 실전문제 풀이

• 1로 만들기
  • 풀이
    • 입력받은 수가 2/3/5로 나누어 떨어지는 경우
    • 최소값은 어떻게 구하지..?
    • dp에 대한 이해가 전반적으로 부족한 듯
    • 해답 봐도 이해 안돼서 당황 -_-
  • 코드(참고)

    #include <iostream>
    #include<algorithm>
    using namespace std;
    
    int d[30001];
    int x;
    
    int main() {
    	cin >> x;
    	for (int i = 2; i <= x; i++) {
    		d[i] = d[i - 1] + 1;
    		if (i % 2 == 0) d[i] = min(d[i], d[i / 2] + 1);
    		if (i % 3 == 0) d[i] = min(d[i], d[i / 3] + 1);
    		if (i % 5 == 0) d[i] = min(d[i], d[i / 5] + 1);
    	}
    	cout << d[x] << endl;
    }

• 개미전사
  • 풀이
    • 전체 중 가장 값이 큰 것을 우선 약탈
    • 해당 인덱스 기준 +-1 인덱스 제외시키고 다음으로 큰 수 약탈?? 근데 이럼 일부 경우의 수 해당xx
    • 다른방법은???

      arr[0]	arr[1]	arr[2]	arr[3]
      1	2	3	4

    • 오른쪽부터 시작한다고 가정하고 현재 arr[2]일 때 나를 포함한 arr[0]을 약탈할건지, 나를 제외한 arr[1]을 약탈할건지 정함.
    • 그니까 항상 이미 지나온 방향을 가지고 결정하는거임. 그래서 처음부터 반복하는거. 표로 그리면 방문할수 있는 마을이 4개 있다고 가정할 때 아래의 그림처럼 풀이할 수 있는 것
      

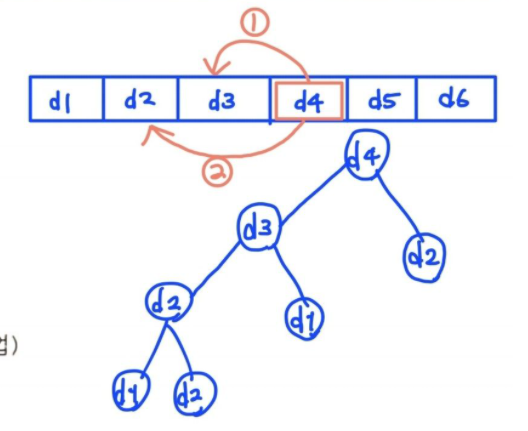
- 코드(참고)
    
    ```cpp
    #include<iostream>
    #include<vector>
    #include<algorithm>
    using namespace std;
    
    int d[100];
    int n;
    vector<int> arr;
    
    int main() {
    	cin >> n;
    	for (int i = 0; i < n; i++) {
    		int x;
    		cin >> x;
    		arr.push_back(x);
    	}
    	d[0] = arr[0];
    
    	d[1] = max(arr[0],arr[1]);
    	for (int i = 2; i < n; i++) {
    		d[i] = max(d[i - 1], d[i - 2] + arr[i]);
    	}
    
    	cout << d[n - 1] << '\n';
    	return 0;
    }
    ```
    

• 바닥공사
  • 풀이
    • 점화식 도출해야 함
    • a[i]=a[i-1]+a[i-2]*2. 그림으로 이해해야 함. 식이 쉬워서 점화식 설명 듣고 코드는 바로 짬
    • 저거 796796으로 나눠주는 이유는 그냥 값이 너무 커지는걸 방지하기 위함이라고 함
    • 점화식 도출해내는게 너무 어렵다. . . ㅠ.ㅠ. . .
  • 코드

    #include<iostream>
    using namespace std;
    int d[1001];
    
    int main() {
    	int x;
    	cin >> x;
    	d[1] = 1;
    	d[2] = 3;
    	for (int i = 3; i <= x; i++) {
    		d[i] = (d[i - 1] + d[i - 2] * 2) % 796796;
    	}
    	cout << d[x] << endl;
    	return 0;
    }

• 효율적인 화폐 구성
  • 풀이
    • 이해중. . .
  • 코드(참고)

    #include<iostream>
    #include<vector>
    #include<algorithm>
    
    using namespace std;
    
    int n, m;
    vector<int> arr;
    
    int main(void) {
        // 정수 N, M을 입력받기
        cin >> n >> m;
    
        // N개의 화폐 단위 정보를 입력 받기
        for (int i = 0; i < n; i++) {
            int x;
            cin >> x;
            arr.push_back(x);
        }
    
        // 한 번 계산된 결과를 저장하기 위한 DP 테이블 초기화
        vector<int> d(m + 1, 10001);
    
        // 다이나믹 프로그래밍(Dynamic Programming) 진행(보텀업)
        d[0] = 0;
        for (int i = 0; i < n; i++) {
            for (int j = arr[i]; j <= m; j++) {
                // (i - k)원을 만드는 방법이 존재하는 경우
                if (d[j - arr[i]] != 10001) {
                    d[j] = min(d[j], d[j - arr[i]] + 1);
                }
            }
        }
    
        // 계산된 결과 출력
        if (d[m] == 10001) { // 최종적으로 M원을 만드는 방법이 없는 경우
            cout << -1 << '\n';
        }
        else {
            cout << d[m] << '\n';
        }
    }