이진탐색
이진탐색은 탐색하고자 하는 범위의 시작점, 끝점, 중간점을 지정하여 찾으려는 데이터와 중간점 위치에 있는 데이터를 반복적으로 비교해서 원하는 데이터를 찾는 탐색방법이다.
이진탐색 트리
- 부모 노드보다 왼쪽 자식 노드보다 작다.
- 부모 노드보다 오른쪽 자식 노드가 크다.
아래의 그림은 이진탐색트리에서 37을 탐색하는 과정이다.
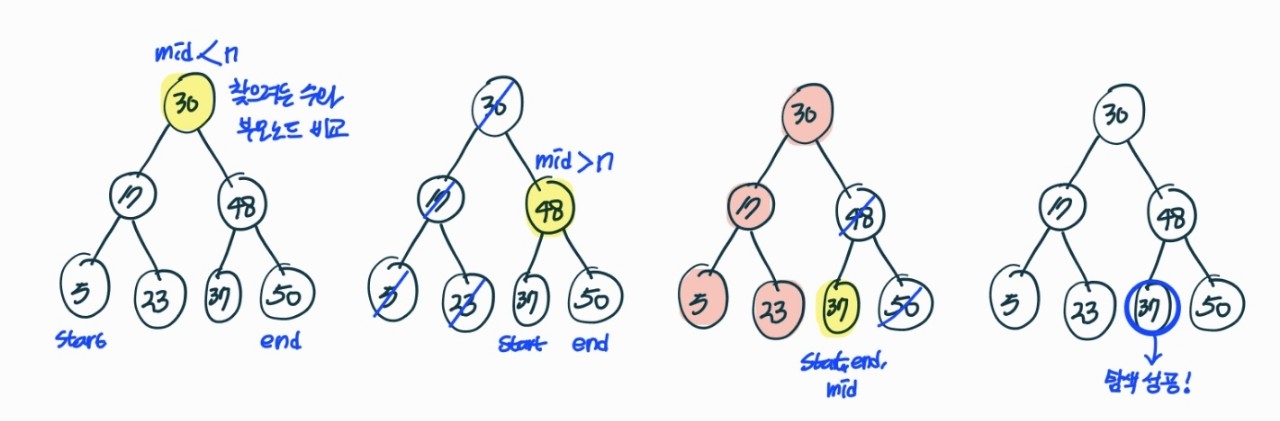
문제풀이
부품 찾기
- 전체 물량을 정렬한다
(start+end)/2로 중간값인 mid를 구한다- mid가 내가 찾는 값과 같으면 탐색을 종료하고 yes를 출력한다
- mid가 내가 찾는 값보다 크면
mid+1,끝으로 범위를 수정한다 - mid가 내가 찾는 값보다 작으면
시작지점,mid-1로 범위를 수정한다 - 처음 과정을 시작지점이 끝보다 커질때까지 반복한다.
#include <iostream>
#include <algorithm>
using namespace std;
int arr[1000001];
int parts[100001];
int n, m;
void search_parts(int start, int end, int part)
{
int mid = (start + end) / 2;
if (start > end)
{
cout << "no" << "\n";
return;
}
if (arr[mid] < part)
search_parts(mid + 1, end, part);
else if (arr[mid] > part)
search_parts(start, mid - 1, part);
else
{
cout << "yes" << "\n";
return;
}
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> arr[i];
}
cin >> m;
for (int i = 0; i < m; i++)
{
cin >> parts[i];
}
sort(arr, arr + n);
for (int i = 0; i < m; i++)
{
search_parts(0, n - 1, parts[i]);
}
}떡볶이 떡 만들기
순차탐색을 이용한 로직은 떠올렸고 답도 멀쩡히 나오지만 이진탐색 파트에 있는 것이 걸리는 문제였다. 잘린 떡의 합을 구하는데 O(N)이고 최악의 경우 O(N)을 배열 안의 가장 큰 값만큼 반복할 수 있다. 따라서 입력받는 자료가 커질수록 복잡도가 높아지는 것을 예상할 수 있었다. 심지어 절단기 높이가 10억까지의 정수라는 것 때문에 이 코드가 틀렸다는 것을 직감했다. 그래서 복잡도를 낮추기 위해 책에서 제공하는 코드를 참고하고 이해했다.
<순차탐색>
- 절단기 높이를 1부터 시작해서 자른 떡 높이의 합이 m과 같거나 큰 동안 반복한다.
- 만약 떡 높이의 합이 m보다 작다면 현재 절단기 높이에서 1을 뺀 값을 출력하고 반복을 중단한다.
<이진탐색>
- 시작과 끝을 0과 10억으로 설정하고 그 중간값을 절단기 높이로 설정한다.
- 잘린 떡의 합계를 구해서 그 값이 m보다 작으면 끝지점을 수정한다.
- 그 값이 m보다 크면 시작지점을 수정한다.
- 시작지점의 값이 끝지점보다 작거나 같은 동안 반복한다.
수정 전
#include <iostream>
using namespace std;
int arr[1000001];
int main()
{
int n, m, leng, sum, ans;
cin >> n >> m;
for (int i = 0; i < n; i++)
{
cin >> arr[i];
}
leng = 1;
while(1)
{
sum = 0;
for (int i = 0; i < n; i++)
{
if (arr[i] - leng >= 0)
sum += arr[i] - leng;
}
if (sum < m)
{
cout << leng - 1 << "\n";
return 0;
}
else
leng++;
}
return 0;
}수정 후
#include <iostream>
#include <vector>
using namespace std;
int n, m;
vector<int> arr;
int main(void) {
cin >> n >> m;
for (int i = 0; i < n; i++)
{
int x;
cin >> x;
arr.push_back(x);
}
int start = 0;
int end = 1e9;
int result = 0;
while (start <= end) {
long long int total = 0;
int mid = (start + end) / 2;
for (int i = 0; i < n; i++)
{
if (arr[i] > mid)
total += arr[i] - mid;
}
if (total < m)
{
end = mid - 1;
}
else {
result = mid;
start = mid + 1;
}
}
cout << result << '\n';
}2630 색종이 만들기
재귀로 풀었다. 스터디 준비하면서 dfs/bfs풀 때 비슷한 유형의 문제들을 많이 겪어봤는데 덕분에 로직은 쉽게 떠올랐다.
- x,y좌표와 한 변의 길이를 함수로 보냄
- 모든 면이 1이면 b카운트, 0이면 w카운트
- 위에 해당되지 않으면 네개의 구역을 다시 함수로 보냄
- 한 변의 길이가 1이 될 때까지 반복
+a)이 문제는 dfs문제랑 결은 비슷하지만 dfs는 아니고 분할정복 문제라고 한다. 얏호
주석은 코드 수정이 필요해서 사용했다.
#include <iostream>
using namespace std;
int arr[129][129];
int n;
int b = 0;
int w = 0;
void dfs(int x, int y, int leng)
{
bool blue, white;
blue = white = true;
if (leng == 1)
{
if (arr[x][y] == 1)
b++;
else
w++;
return;
}
for (int i = x; i < x + leng; i++)
{
for (int j = y; j < y + leng; j++)
{
if (arr[i][j] == 1)
white = false;
if (arr[i][j] == 0)
blue = false;
}
}
if (white == true)
{
w++;
//cout << "하얀색이 추가됨" << endl;
return;
}
if (blue == true)
{
b++;
//cout << "파란색이 추가됨" << endl;
return;
}
int i = leng / 2;
dfs(x, y, i);
dfs(x, y + i, i);
dfs(x + i, y, i);
dfs(x + i, y + i, i);
}
int main()
{
cin >> n;
for (int i = 0; i < n; i++)
{
for (int j = 0; j < n; j++)
cin >> arr[i][j];
}
dfs(0, 0, n);
cout << w << "\n" << b << "\n";
return 0;
}다이나믹 프로그래밍
다이나믹 프로그래밍은 하나의 큰 문제를 해결하기 위해 풀리는 작은 문제들이 서로 연결된 경우를 의미한다. 따라서 인접한 항들 사이의 관계식인 점화식을 이용한다. 메모이제이션도 dp를 위한 기법 중 하나이지만 메모이제이션 한 자료를 다시 사용해야 dp라고 할 수 있고 단순히 저장만 하는 경우 dp가 아니다. 다이나믹 프로그래밍에는 바텀업 방식과 탑다운 방식이 있다.
- 바텀업 방식
반복문DP 테이블작은 문제를 이용해서 큰 문제 해결 - 탑다운 방식
재귀함수메모이제이션큰 문제에서 시작해서 작은 문제들을 해결
책에서는 재귀함수의 스택버퍼 문제로 바텀업 방식을 추천한다.
문제풀이
1로 만들기
이 문제와 비슷한 문제를 백준에서 풀어본 기억이 있다. 그 때의 로직을 되살려서 코드를 작성했으나 이전의 문제와 조건이 달라서 한번 코드 순서를 뒤집어서 짰다. 교재에 있는 로직을 참고했는데 너무 깔끔한 로직이라 감탄함.
수정 전
#include <iostream>
#include <algorithm>
using namespace std;
int arr[30001];
int main()
{
int x;
cin >> x;
arr[2] = 1;
if (x > 2)
{
for (int i = 3; i <= x; i++)
{
if (i % 2 == 0 || i % 3 == 0 || i % 5 == 0)
{
arr[i] = min(arr[i / 2] + 1, arr[i / 3] + 1);
arr[i] = min(arr[i], arr[i / 5] + 1);
}
else if (i % 5 == 0)
arr[i] = min(arr[i / 5] + 1, arr[i - 1] + 1);
else if (i % 3 == 0)
arr[i] = min(arr[i / 3] + 1, arr[i - 1] + 1);
else if (x % 2 == 0)
arr[i] = min(arr[i / 2] + 1, arr[i - 1] + 1);
else
arr[i] = arr[i - 1] + 1;
}
}
cout << arr[x] << "\n";
}수정 후
#include <iostream>
using namespace std;
int arr[30001];
int main()
{
int x;
cin >> x;
arr[2] = 1;
if (x > 2)
{
for (int i = 3; i <= x; i++)
{
arr[i] = arr[i - 1] + 1;
if (i % 2 == 0)
arr[i] = min(arr[i], arr[i / 2] + 1);
if (i % 3 == 0)
arr[i] = min(arr[i], arr[i / 3] + 1);
if (i % 5 == 0)
arr[i] = min(arr[i], arr[i / 5] + 1);
}
}
cout << arr[x] << "\n";
}개미 전사
이동할 때마다 현재 위치의 식량 총합을 받는 배열을 만든다는 아이디어는 책을 보고 알았다. 책의 로직대로 sum[0]과 sum[1]의 값을 미리 넣고 그 이후에 다음 값들을 예상해보면 sum[2]는 sum[0]+arr[2]와 sum[1] 중 더 큰 값으로 결정된다. 이걸 점화식으로 표현하면 sum[i]=max(sum[i-1], sum[i-2]+arr[i])가 된다.
#include <iostream>
using namespace std;
int arr[101];
int sum[101];
int main()
{
int n;
cin >> n;
for (int i = 0; i < n; i++)
{
cin >> arr[i];
}
sum[0] = arr[0];
sum[1] = max(arr[0], arr[1]);
for (int i = 2; i < n; i++)
{
sum[i] = max(sum[i - 1], sum[i - 2] + arr[i]);
}
cout << sum[n - 1] << "\n";
return 0;
}바닥 공사
머리로는 받아들일 수 있는데 이걸 직접 점화식 생각해내려고 하니 도저히 떠오르는게 없었다. 실전에서 이 문제를 어떻게 풀지? 코드는 정말 간단했는데 위의 문제들과는 달리 해설을 봐도 이해만 될뿐 다음번 풀이에 응용하지 못할 것 같다.
#include <iostream>
using namespace std;
int arr[1001];
int main()
{
int x;
cin >> x;
arr[1] = 1;
arr[2] = 3;
for (int i = 3; i <= x; i++)
{
arr[i] = arr[i - 1] + arr[i - 2] * 2;
}
cout << arr[x] << "\n";
}효율적인 화폐 구성
이해중
#include <iostream>
#include <vector>
using namespace std;
int n, m;
vector<int> arr;
int main(void)
{
cin >> n >> m;
for (int i = 0; i < n; i++) {
int x;
cin >> x;
arr.push_back(x);
}
vector<int> d(m + 1, 10001);
d[0] = 0;
for (int i = 0; i < n; i++)
{
for (int j = arr[i]; j <= m; j++)
{
if (d[j - arr[i]] != 10001)
d[j] = min(d[j], d[j - arr[i]] + 1);
}
}
if (d[m] == 10001)
{
cout << -1 << '\n';
}
else {
cout << d[m] << '\n';
}
}9095 1, 2, 3 더하기
dp 카테고리에서 찾은 문제였는데 점화식은 찾았으나 입증할 방법이 없어서 조금 더 신빙성이 있는 dfs로 풀었다.
내가 찾은 점화식은 n이 4이상일 때 dp(n)=dp(n-1)+dp(n-2)+dp(n-3)이었는데 아마 dp 카테고리에 있으니 맞을거 같다.
dfs는 입력받은 n을 최대 버퍼로 생각하고 1, 2, 3을 n이 될 때까지 더해줬다. 반복문을 돌릴 때 주의한 부분은 1, 2, 3을 더했을 때 n을 넘는 경우가 있으므로 그 경우는 조건문을 걸어서 처리했다.
#include <iostream>
using namespace std;
int N;
int cnt=0;
void dfs(int n)
{
if(n==N)
{
cnt++;
return;
}
for(int i=1;i<=3;i++)
{
if(n+i<=N)
dfs(n+i);
}
}
int main()
{
int number;
cin>>number;
for(int i=0;i<number;i++)
{
cin>>N;
dfs(0);
cout<<cnt<<"\n";
cnt=0;
}
return 0;
}

