구간 합

구간 합은 합 배열을 이용하여 시간 복잡도를 더 줄이기 위해 사용하는 특수한 목적의 알고리즘이다.

핵심 이론

합 배열

먼저, 합 배열을 구해야 한다. 배열 A가 있을 때 합 배열 S는 다음과 같이 정의한다.

S[i] = A[0] + A[1] + A[2] + ... + A[i-1] + A[i]; // A[0] 부터 A[i]까지의 합

합 배열은 기존 배열을 전처리한 배열이다. 합 배열을 미리 구해 놓으면 기존 배열의 일정 범위 합을 구하는 시간 복잡도가 O(N)에서 O(1)로 감소한다.

	0	1	2	3	4	5
배열 A	15	13	10	7	3	12
합 배열 S	15	28	38	45	48	60

배열의 합을 합 배열 없이 구하는 경우 최악의 경우 i가 0이고 j가 n인 경우 시간 복잡도는 O(N)이다.

다음과 같은 공식으로 합 배열을 만들 수 있다.

S[i] = S[i-1] + A[i];

2차원 합 배열

2차원 합 배열은 (1, 1)에서 (i, j) 까지의 누적합을 저장한다. 계산하는 방법은 아래와 같다.

S[x][y] = S[x-1][y] + S[x][y-1] - S[x-1][y-1] + A[x][y]

표를 살펴보자. 이 표는 원본 값을 담은 A표이다.

y\x	1	2	3	4
1	1	2	3	4
2	2	3	4	5
3	3	4	5	6
4	4	5	6	7

여기서 S[2][2]를 계산해보자. S[2][2] = S[1][2] + S[2][1] - S[1][1] + S[2][2]이다. 3+6-1+6=14, 즉 14가 된다. 어떻게 이런 결과가 나왔을까? 그림으로 이해해보자.

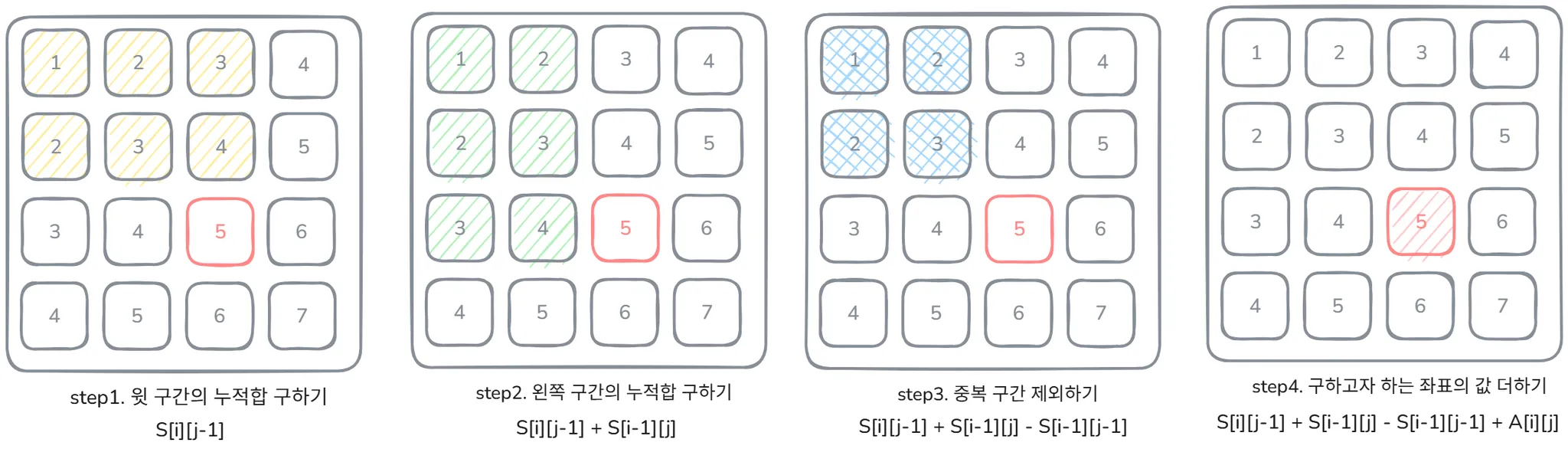
이렇게 순서대로 구한 값들을 포개어 보면 아래와 같이 보인다. (1,1)부터 (i,j)까지의 모든 값이 저장되어 보인다.

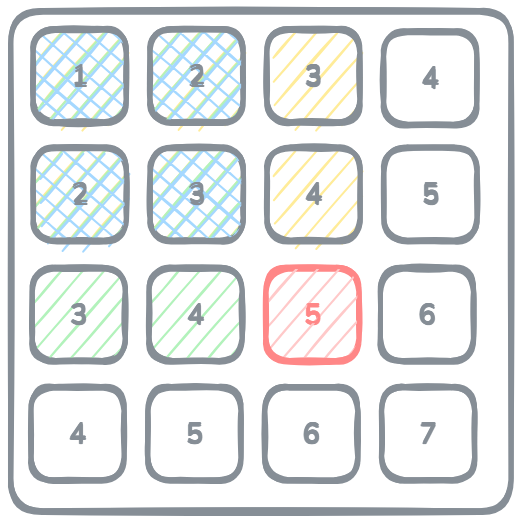
구간 합

합 배열을 이용하면 구간의 합도 쉽게 구할 수 있다.

S[j] - S[i-1]; // i에서 j까지 구간 합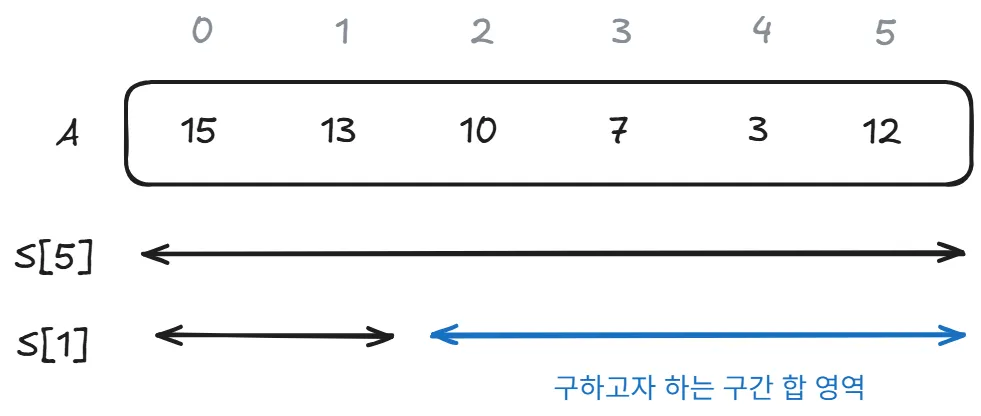

A[2]-A[5] 까지의 구간 합을 구하고 싶다면 S[5]에서 S[1]을 빼면 된다.

관련 문제

• BOJ11659
• BOJ11660
• BOJ10986