그래프 이론
서로소 집합
서로소 집합이란 공통원소가 없는 두 집합을 의미함.
서로소 집합 자료구조란 서로소 부분 집합들로 나누어진 원소들의 데이터를 처리하기 위한 자료구조이다.
- union 연산하여 서로 연결된 두 노드 a, b를 확인한다
- a와 b의 루트노드 a' b' 를 각각 찾는다
- a'를 b'의 부모 노드로 설정한다
- 모든 union 연산을 처리할 때까지 처음 과정을 반복한다
서로소 집합 알고리즘 코드
#include <iostream>
using namespace std;
// 노드의 개수(V)와 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
int v, e;
int parent[100001]; // 부모 테이블 초기화하기
// 특정 원소가 속한 집합을 찾기
int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) return x;
return findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
int main(void) {
cin >> v >> e;
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
// Union 연산을 각각 수행
for (int i = 0; i < e; i++) {
int a, b;
cin >> a >> b;
unionParent(a, b);
}
// 각 원소가 속한 집합 출력하기
cout << "각 원소가 속한 집합: ";
for (int i = 1; i <= v; i++) {
cout << findParent(i) << ' ';
}
cout << '\n';
// 부모 테이블 내용 출력하기
cout << "부모 테이블: ";
for (int i = 1; i <= v; i++) {
cout << parent[i] << ' ';
}
cout << '\n';
}위의 알고리즘은 시간 복잡도가 최대 O(VM)이므로 효율이 떨어진다. 경로 압축 기법을 적용해 복잡도를 개선시킬 수 있다. findParent함수를 재귀적으로 호출한 뒤에 부모 테이블값을 갱신하는 기법임.
#include <iostream>
using namespace std;
// 노드의 개수(V)와 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
int v, e;
int parent[100001]; // 부모 테이블 초기화
// 특정 원소가 속한 집합을 찾기
int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) return x;
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
int main(void) {
cin >> v >> e;
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
// Union 연산을 각각 수행
for (int i = 0; i < e; i++) {
int a, b;
cin >> a >> b;
unionParent(a, b);
}
// 각 원소가 속한 집합 출력하기
cout << "각 원소가 속한 집합: ";
for (int i = 1; i <= v; i++) {
cout << findParent(i) << ' ';
}
cout << '\n';
// 부모 테이블 내용 출력하기
cout << "부모 테이블: ";
for (int i = 1; i <= v; i++) {
cout << parent[i] << ' ';
}
cout << '\n';
}서로소 집합 알고리즘 응용
서로소 집합은 무방향 그래프 내에서 사이클을 판별할 때 사용할 수 있다. (방향 그래프의 사이클 판별은 DFS로 가능)
그래프에 포함되어 있는 모든 간선을 하나식 확인하여 간선에 대해 union 및 find 함수를 호출하는 방식으로 동작한다.
- 각 간선을 확인하며 두 노드의 루트 노드를 확인한다
- 루트 노드가 서로 다르다면 두 노드에 대하여 union 연산을 수행한다
- 루트 노드가 서로 같다면 사이클이 발생한 것이다
- 그래프에 포함되어 있는 모든 간선에 대해 1번 과정을 반복한다
#include <iostream>
using namespace std;
// 노드의 개수(V)와 간선(Union 연산)의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
int v, e;
int parent[100001]; // 부모 테이블 초기화
// 특정 원소가 속한 집합을 찾기
int findParent(int x) {
// 루트 노드가 아니라면, 루트 노드를 찾을 때까지 재귀적으로 호출
if (x == parent[x]) return x;
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
void unionParent(int a, int b) {
a = findParent(a);
b = findParent(b);
if (a < b) parent[b] = a;
else parent[a] = b;
}
int main(void) {
cin >> v >> e;
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++) {
parent[i] = i;
}
bool cycle = false; // 사이클 발생 여부
for (int i = 0; i < e; i++) {
int a, b;
cin >> a >> b;
// 사이클이 발생한 경우 종료
if (findParent(a) == findParent(b)) {
cycle = true;
break;
}
// 사이클이 발생하지 않았다면 합집합(Union) 연산 수행
else {
unionParent(a, b);
}
}
if (cycle) {
cout << "사이클이 발생했습니다." << '\n';
}
else {
cout << "사이클이 발생하지 않았습니다." << '\n';
}
}신장트리
신장트리는 하나의 그래프가 모든 노드를 포함하면서 사이클이 존재하지 않는 부분 그래프를 의미한다.
크루스칼 알고리즘
가장 적은 비용으로 신장트리를 만들 수 있는 알고리즘이다. 모든 간선을 정렬한 뒤 가장 거리가 짧은 간선부터 집합에 포함시키면 된다. 다만 사이클이 발생되는 경우 집합에 포함시키지 않는다.
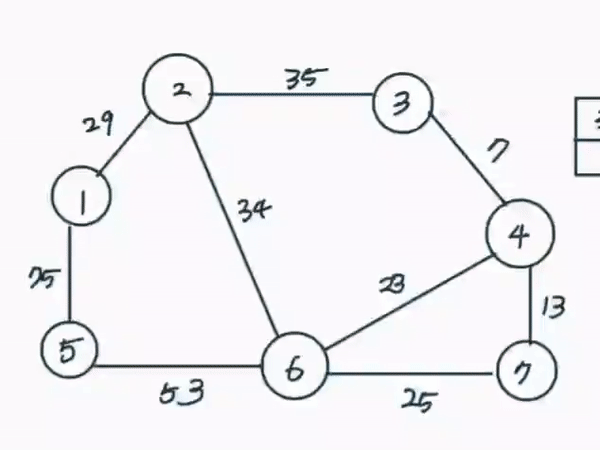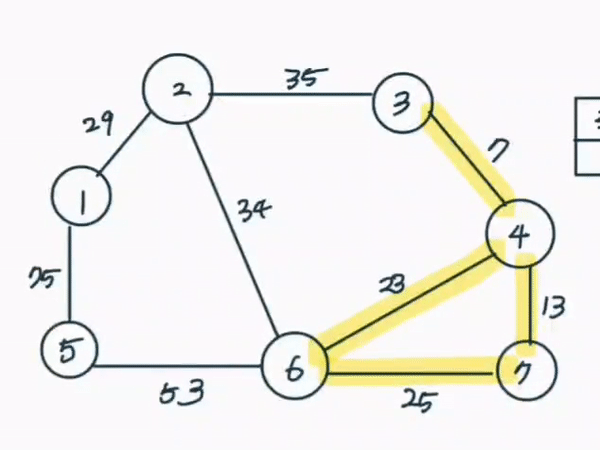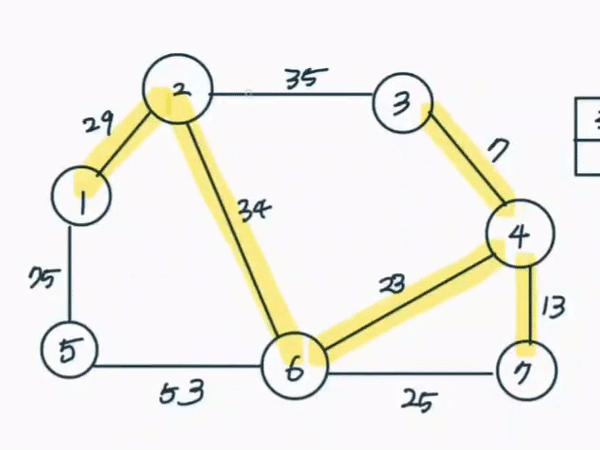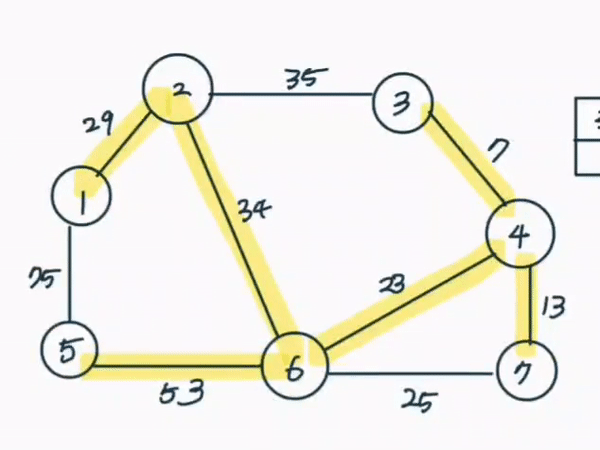
- 간선데이터를 비용에 따라 오름차순 정렬한다
- 간선을 하나씩 확인하며 현재 간선이 사이클을 발생시키는지 확인한다
- 사이클 미발생 : 최소 신장 트리에 포함
- 사이클 발생 : 최소 신장 트리에 미포함
- 모든 간선에 대해 뒤의 과정을 반복한다
위의 영상이 크루스칼 알고리즘에 따라 신장트리가 완성되는 과정을 그린 것이다.
크루스칼 알고리즘 코드
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int v, e;
int parent[100001];
// 모든 간선을 담을 리스트와, 최종 비용을 담을 변수
vector<pair<int, pair<int, int> > > edges;
int result = 0;
// 특정 원소가 속한 집합을 찾기
int findParent(int x)
{
if (x == parent[x])
return x;
return parent[x] = findParent(parent[x]);
}
// 두 원소가 속한 집합을 합치기
void unionParent(int a, int b)
{
a = findParent(a);
b = findParent(b);
if (a < b)
parent[b] = a;
else
parent[a] = b;
}
int main(void)
{
cin >> v >> e;
// 부모 테이블상에서, 부모를 자기 자신으로 초기화
for (int i = 1; i <= v; i++)
parent[i] = i;
// 모든 간선에 대한 정보를 입력 받기
for (int i = 0; i < e; i++)
{
int a, b, cost;
cin >> a >> b >> cost;
// 비용순으로 정렬하기 위해서 튜플의 첫 번째 원소를 비용으로 설정
edges.push_back({cost, {a, b}});
}
// 간선을 비용순으로 정렬
sort(edges.begin(), edges.end());
// 간선을 하나씩 확인하며
for (int i = 0; i < edges.size(); i++)
{
int cost = edges[i].first;
int a = edges[i].second.first;
int b = edges[i].second.second;
// 사이클이 발생하지 않는 경우에만 집합에 포함
if (findParent(a) != findParent(b))
{
unionParent(a, b);
result += cost;
}
}
cout << result << '\n';
}위상정렬
위상정렬은 방향 그래프의 모든 노드를 방향성에 거스르지 않도록 순서대로 나열하는 것이다.
| 진입차수 | 진출차수 |
|---|---|
| 특정 노드로 들어오는 간선의 개수 | 특정 노드를 거쳐 나가는 간선의 개수 |
- 진입차수가 0인 노드를 큐에 넣는다
- 큐가 빌 때까지 아래를 반복한다
- 큐에서 원소를 꺼내 해당 노드에서 출발하는 간선을 그래프에서 제거한다
- 새롭게 진입차수가 0이 된 노드를 큐에 넣는다
위상정렬 알고리즘 코드
#include <iostream>
#include <vector>
#include <queue>
using namespace std;
// 노드의 개수(V)와 간선의 개수(E)
// 노드의 개수는 최대 100,000개라고 가정
int v, e;
// 모든 노드에 대한 진입차수는 0으로 초기화
int indegree[100001];
// 각 노드에 연결된 간선 정보를 담기 위한 연결 리스트 초기화
vector<int> graph[100001];
// 위상 정렬 함수
void topologySort()
{
vector<int> result; // 알고리즘 수행 결과를 담을 리스트
queue<int> q; // 큐 라이브러리 사용
// 처음 시작할 때는 진입차수가 0인 노드를 큐에 삽입
for (int i = 1; i <= v; i++)
{
if (indegree[i] == 0)
q.push(i);
}
// 큐가 빌 때까지 반복
while (!q.empty())
{
// 큐에서 원소 꺼내기
int now = q.front();
q.pop();
result.push_back(now);
// 해당 원소와 연결된 노드들의 진입차수에서 1 빼기
for (int i = 0; i < graph[now].size(); i++)
{
indegree[graph[now][i]] -= 1;
// 새롭게 진입차수가 0이 되는 노드를 큐에 삽입
if (indegree[graph[now][i]] == 0)
q.push(graph[now][i]);
}
}
// 위상 정렬을 수행한 결과 출력
for (int i = 0; i < result.size(); i++)
{
cout << result[i] << ' ';
}
}
int main(void) {
cin >> v >> e;
// 방향 그래프의 모든 간선 정보를 입력 받기
for (int i = 0; i < e; i++)
{
int a, b;
cin >> a >> b;
graph[a].push_back(b); // 정점 A에서 B로 이동 가능
// 진입 차수를 1 증가
indegree[b] += 1;
}
topologySort();
}문제풀이
팀 결성
위에서 공부한 내용 거의 긁어왔다. find와 union연산 함수를 만들어서 각각 필요할 때 해당 함수가 호출되도록 작성했다.
#include <iostream>
using namespace std;
int v, e;
int parent[100001];
int findParent(int x)
{
if (parent[x] == x)
return x;
else
return findParent(parent[x]);
}
void unionParent(int a, int b)
{
a = findParent(a);
b = findParent(b);
if (a < b)
parent[b] = a;
else
parent[a] = b;
}
int main() {
cin >> v >> e;
for (int i = 0; i <= v; i++)
parent[i] = i;
for (int i = 0; i < e; i++)
{
int op, a, b;
cin >> op >> a >> b;
if (op == 0)
unionParent(a, b);
else
{
if (findParent(a) == findParent(b))
cout << "YES";
else
cout << "NO";
}
}
}도시 분할 계획
도무지 감을 못 잡겠어서 책의 해설을 봤다. 크루스칼 알고리즘을 사용해서 최소 비용 신장트리를 만든 뒤에 가장 비용이 큰 간선을 삭제한다. 트리는 사이클이 없기 때문에 하나의 간선을 삭제하게 되면 두개의 트리로 나눠지게 된다.
해설 보니까 생각해보니 노드 하나만 덜렁 있어도 상관없었는데 왜 그걸 생각 못했을까 싶다-_-
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int parent[100001];
int n, m;
long long ans = 0;
int M = 0;
vector <pair<int, pair<int, int>>> edge;
int find(int x)
{
if (parent[x] == x)
return x;
return parent[x] = find(parent[x]);
}
int main()
{
int count = 0;
cin >> n >> m;
for (int i = 1; i <= n; i++)
parent[i] = i;
int a, b, c;
for (int i = 0; i < m; i++)
{
cin >> a >> b >> c;
edge.push_back({ c,{a,b} });
}
sort(edge.begin(), edge.end());
for (int i = 0; i < edge.size(); i++)
{
if (count == n - 1)
break;
pair<int, pair<int, int >> temp = edge[i];
int tmp1 = find(temp.second.first);
int tmp2 = find(temp.second.second);
if (tmp1 == tmp2)
continue;
parent[tmp2] = tmp1;
ans += temp.first;
M = max(M, temp.first);
}
cout << ans - M;
return 0;
}커리큘럼
9372 상근이의 여행

처음에 문제를 잘못보고 최소비용을 구하는건줄 알았는데 다시 보니 비행기 종류의 개수를 출력하는 문제였다. ㅋㅋ날먹같아서 양심에 찔리는데 최소비용 신장트리는 노드-1개의 간선을 이동하면 구할 수 있다.
크루스칼 알고리즘을 백지에 직접 풀기는 어려울 것 같아서 쉬운 문제부터 풀어봤는데 아무래도 난이도 있는 문제도 직접 풀어봐야겠다.
#include <iostream>
using namespace std;
int main() {
int t, n, m;
cin >> t;
for (int i = 0; i < t; i++)
{
cin >> n >> m;
for (int j = 0; j < m; j++)
{
int a, b;
cin >> a >> b;
}
cout << n - 1 << endl;
}
return 0;
}
