📌 문제

Lv1. 소수 만들기

주어진 숫자 중 3개의 수를 더했을 때 소수가 되는 경우의 개수를 구하려고 합니다. 숫자들이 들어있는 배열 nums가 매개변수로 주어질 때, nums에 있는 숫자들 중 서로 다른 3개를 골라 더했을 때 소수가 되는 경우의 개수를 return 하도록 solution 함수를 완성해주세요.

✔️ 제한사항

• nums에 들어있는 숫자의 개수는 3개 이상 50개 이하입니다.
• nums의 각 원소는 1 이상 1,000 이하의 자연수이며, 중복된 숫자가 들어있지 않습니다.

✏️ 입출력

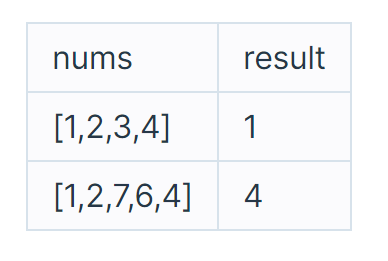
1. 입출력 예 #1 :
   [1,2,4]를 이용해서 7을 만들 수 있습니다.
   
   
2. 입출력 예 #2 :
   [1,2,4]를 이용해서 7을 만들 수 있습니다.
   [1,4,6]을 이용해서 11을 만들 수 있습니다.
   [2,4,7]을 이용해서 13을 만들 수 있습니다.
   [4,6,7]을 이용해서 17을 만들 수 있습니다.

💡 코드

✅ 재귀 함수을 사용해서 문제를 풀어보았다. 한 요소를 더하고, 다음 요소에 대한 합을 구하기 위해 dfs(depth+1, i+1, nums)를 호출하였다. 이 때, 같은 수를 여러 번 더하면 안되므로 재귀 함수가 호출될 때마다 새로운 시작 인덱스 idx를 전달받아 해당 인덱스부터 반복문을 돌려야 한다.

depth = 3이면 3개의 수를 더했다는 뜻이므로 세 수의 합이 소수인지 판별해야 한다. 세 수의 합 sum을 2부터 sum의 제곱근까지 나머지 연산을 수행하였을 때, 하나라도 나누어 떨어지게 하는 값이 있으면 소수가 아니므로 즉시 함수를 종료시킨다. 무사히 반복문을 돌았으면 sum은 소수라는 뜻이므로 cnt를 1 증가시키고 함수를 종료한다.

함수가 종료되어 재귀 호출 시점으로 돌아오면 다음 경우의 수를 구해야 하는데, 이 때 이번 인덱스의 값이 누적된 sum을 사용하면 안되므로 더해줬던 값을 다시 빼서 이전 값으로 초기화 시킨다. 해당 반복문을 모두 돌면 또 그 이전의 재귀 호출 시점으로 돌아가 해당 과정을 반복한다.

class Solution {
    
    static int cnt = 0;
    static int sum = 0;
    
    public int solution(int[] nums) {
        
        dfs(0, 0, nums);
        return cnt;
    }
    
    static void dfs(int depth, int idx,int[] nums) {
        
        if(depth == 3) {
            for(int i=2;i<=(int)Math.sqrt(sum);i++) {
                if(sum % i == 0) return;
            }
            cnt++; return;
        }
        
        for(int i=idx;i<nums.length;i++) {
            sum += nums[i];
            dfs(depth+1, i+1, nums);
            sum -= nums[i];
        }
        return;
    }
}

✅ 재귀 함수가 아닌 for문으로도 풀어봤다! 4중 for문 때문에 머리가 어지럽긴 한데 그냥 봤을 때는 이 코드가 눈에 확 잘 들어오기는 하는 것 같다,,

class Solution {
    public int solution(int[] nums) {
        
        int cnt = 0;
        
        for(int i=0;i<nums.length-2;i++) {
            for(int j=i+1;j<nums.length-1;j++) {
                for(int k=j+1;k<nums.length;k++) {
                    int sum = nums[i] + nums[j] + nums[k];
                    boolean isPrime = true;
                    
                    for(int l=2;l<=(int)Math.sqrt(sum);l++) {
                        if(sum % l == 0) {
                            isPrime = false; break;
                        }
                    }
                    if(isPrime) cnt++;
                }
            }
        }
 
        return cnt;
    }
}