GitHub

01 연속형 변수 다루기

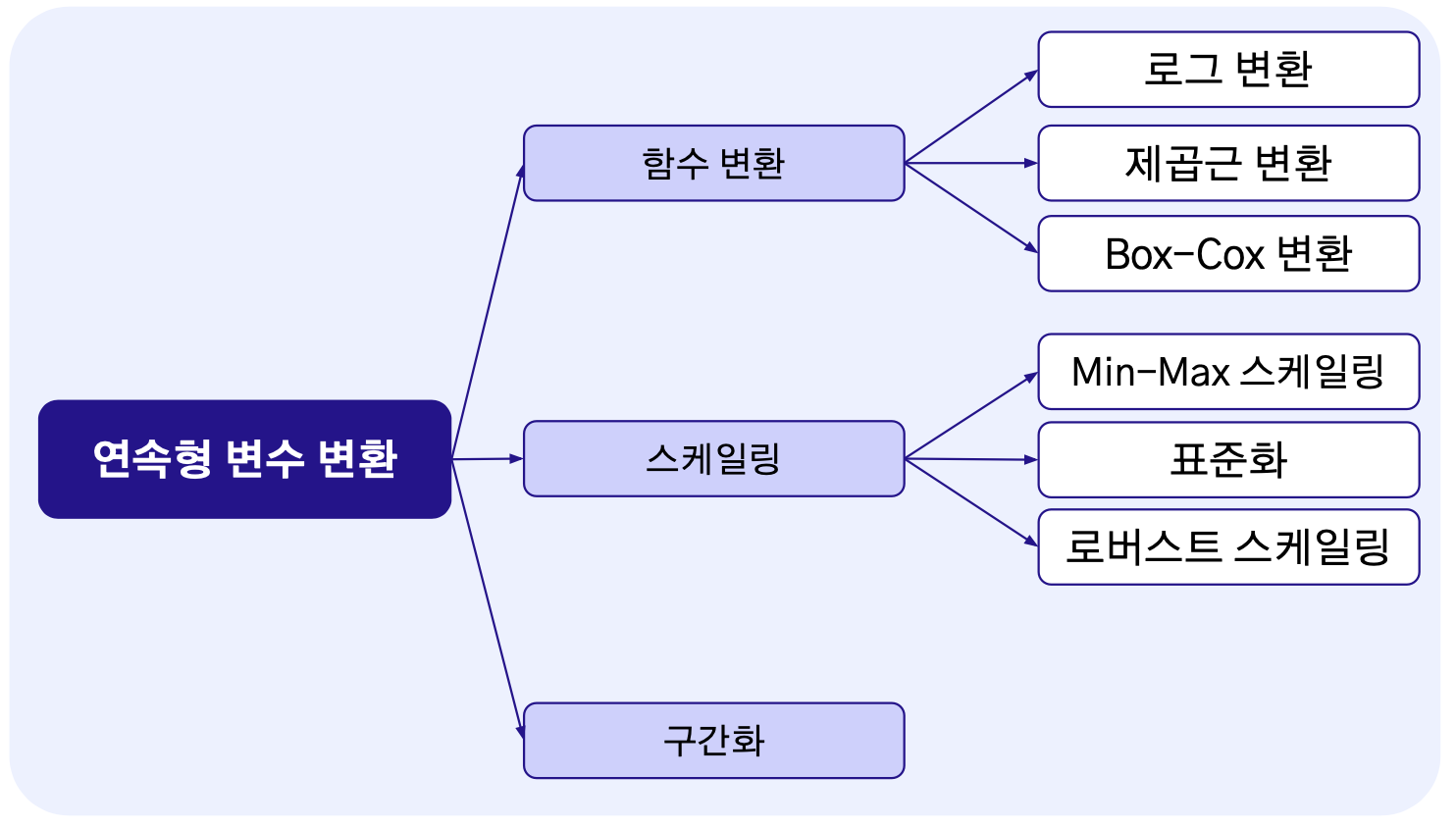
1.1 함수 변환

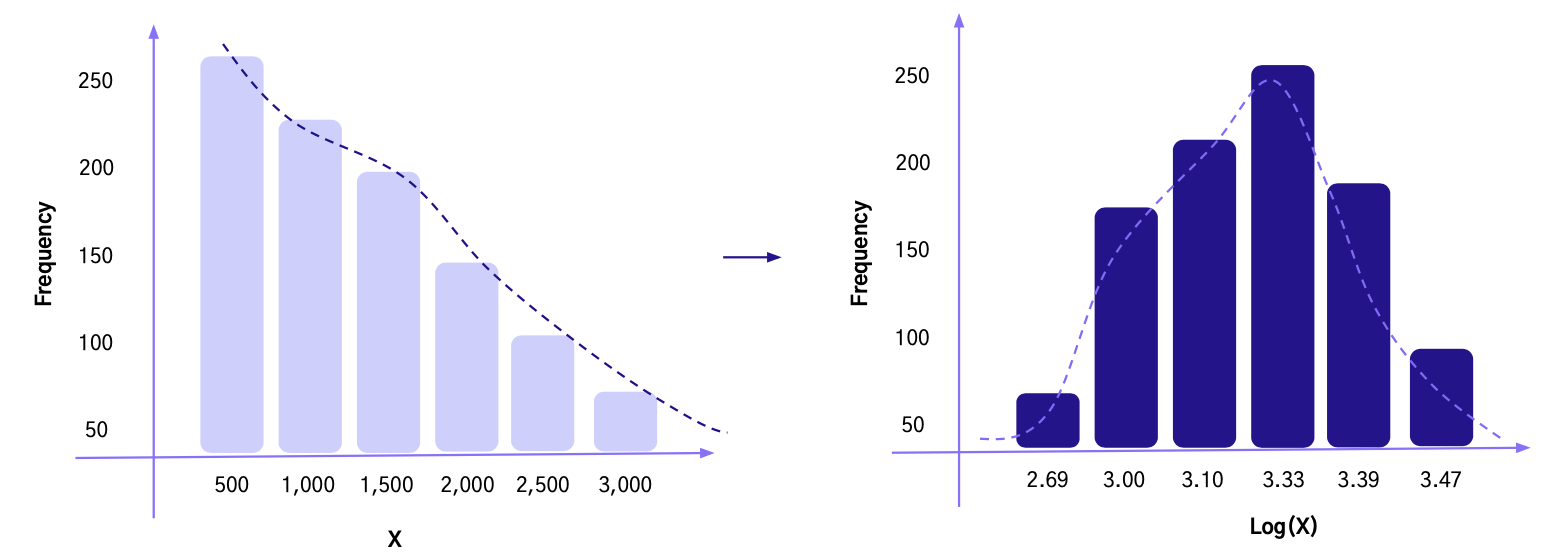
로그 변환

• 비대칭(Right-Skewed)된 임의의 분포를 정규분포에 가깝게 전환시키는데 도움
• 데이터의 정규성은 모델(회귀)의 성능을 향상시키는데 도움
• 데이터의 스케일을 작게 만들어 데이터 간의 편차를 줄이는 효과
• 데이터의 이상치 완화에도 효율적이지만 0이나 음수 적용 불가능

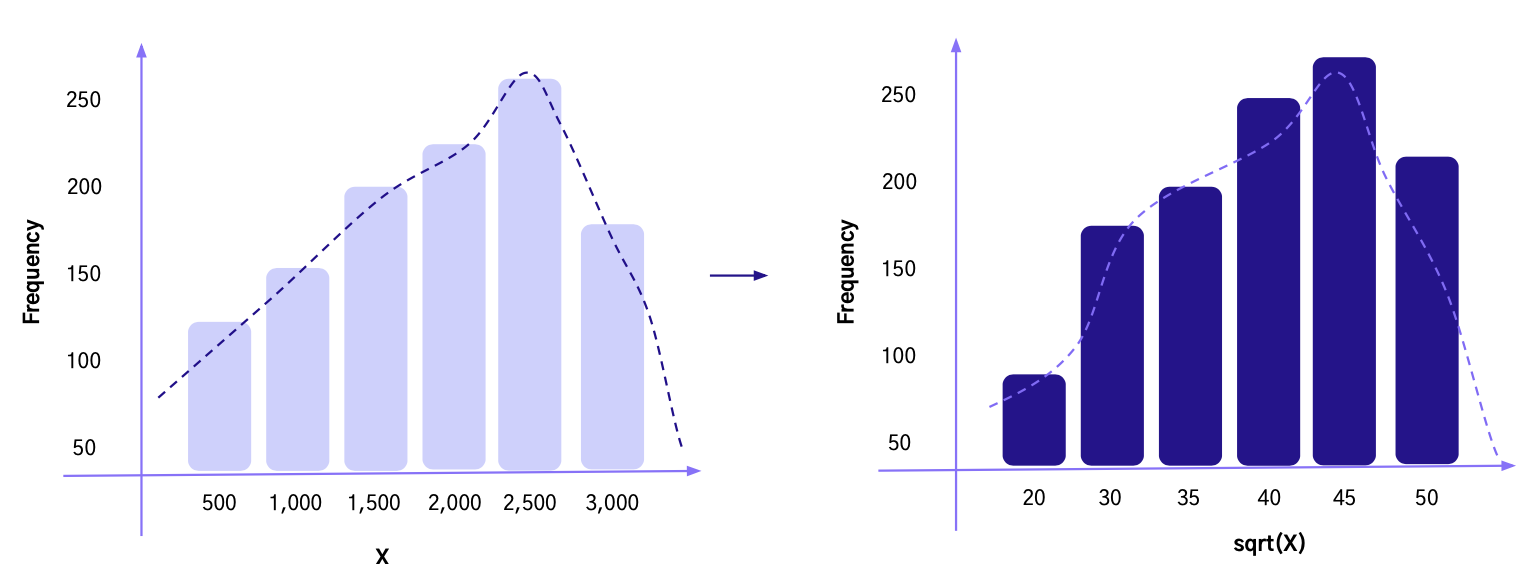
제곱근 변환

• 변수에 제곱근을 적용하여 전환
• 제곱근 변환의 효과는 앞선 로그 변환과 유사 (정규성, 선형관계 생성, 데이터 스케일 축소, 이상치 제거)
• 로그 변환과의 차이점은 변환 시 데이터 편차의 강도
• 비대칭이 (Right-Skewed) 강한 경우 로그 변환, 약한 경우 제곱근 변환이 유리
• 왼쪽으로 치우쳐진 데이터 분포에 활용 시 더 치우치는 부작용 발생

Box - Cox 변환

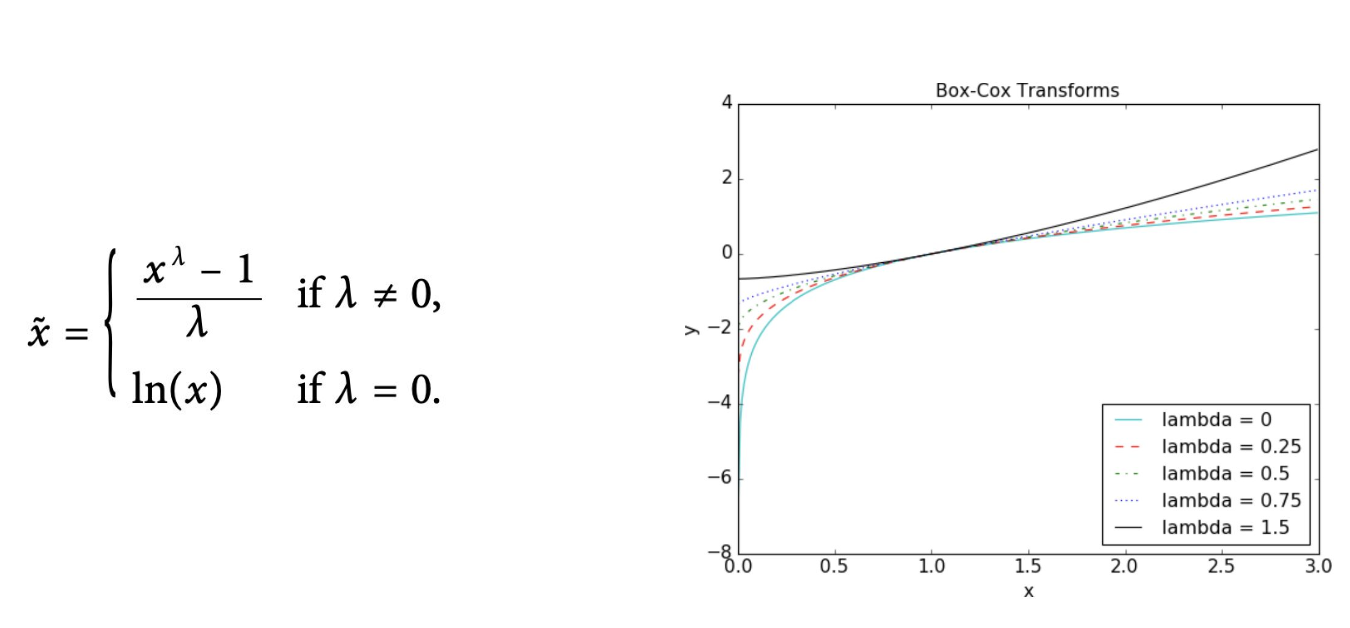
• 람다(λ) 파라미터 값을 통해 다양한 변환을 하는 방법
• 목적에 맞게 최적 람다(λ) 파라미터 값을 찾는 것이 중요

1.2 스케일링

스케일링을 통해서 동일한 수치 범위로 변경

• 예) 데이터의 독립변수는 연속형 변수인 키와 몸무게로 구성되어 있다고 가정
• 키는 170(cm), 몸무게는 56(kg)일 때, 스케일의 차이가 존재

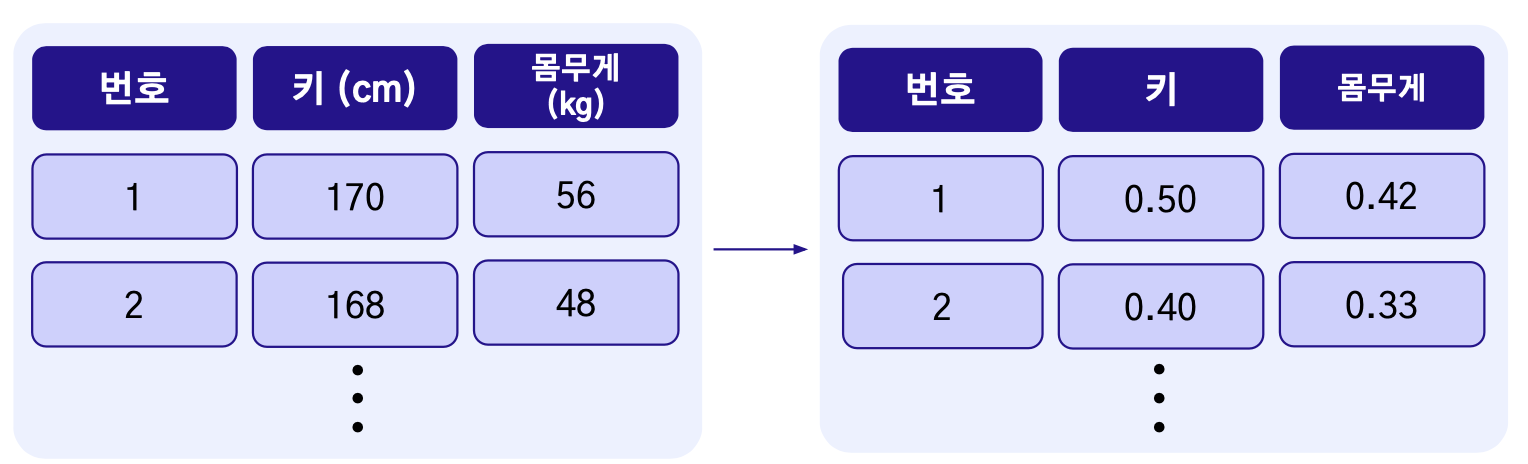
필요한 이유

• 수치형 독립 변수들의 수치 범위가 다르게 존재하면 종속 변수에 각기 다르게 영향을 미침
• 수치 범위가 큰 변수일수록 다른 변수에 비해 더 중요하게 인식될 수 있음
• 독립 변수들의 영향력을 동등하게 변환시켜 KNN과 같은 거리기반 알고리즘에 효과
  ● KNN은 벡터간 거리(유클리드&맨하튼 거리법)를 측정하여 데이터를 분류하는 방식
  ● 변수들이 동일한 범위로 스케일링이 되어 있지 않다면, 결과가 올바르지 않은 리스크 존재

Min-Max 스케일링

• 연속형 변수의 수치 범위를 0-1 사이로 전환

• 각기 다른 연속형 변수의 수치 범위를 통일할 때 사용

• 최소, 최대값을 기준으로 데이터의 상대적 위치를 구성
  

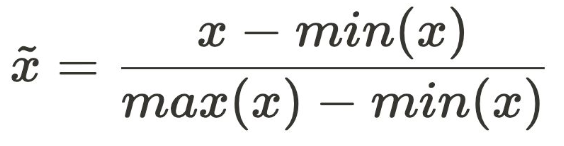
• Min-Max 스케일링은 모든 수치 범위가 같아지므로 이상치에 취약한 부분이 존재
  ● 예) 1,000개의 관측치 중에 999개는 0~30 사이의 범위에 분포해 있지만, 나머지 1개의 값이 100인 경우

표준화(Standardization)

• 변수의 수치 범위(스케일)를 평균이 0, 표준편차가 1이 되도록 변경(Z-score)
• 평균과의 거리를 표준편차로 나누기(정규분포의 표준화 과정)
• 즉, 평균에 가까워질수록 0으로, 평균에서 멀어질수록 큰 값으로 변환

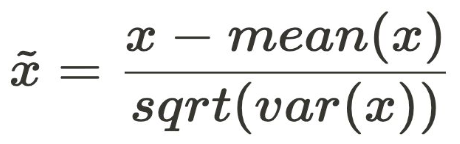
• Min-Max 스케일링과 마찬가지로 변수들의 수치 범위를 축소시키기 때문에 거리기반 알고리즘에서 장점

Robust Scaling

• IQR을 기준으로 변환 (중앙값과의 거리를 IQR로 나누기)
• 즉, 중앙값에 가까워질수록 0으로, 중앙값에서 멀어질수록 큰 값으로 변환

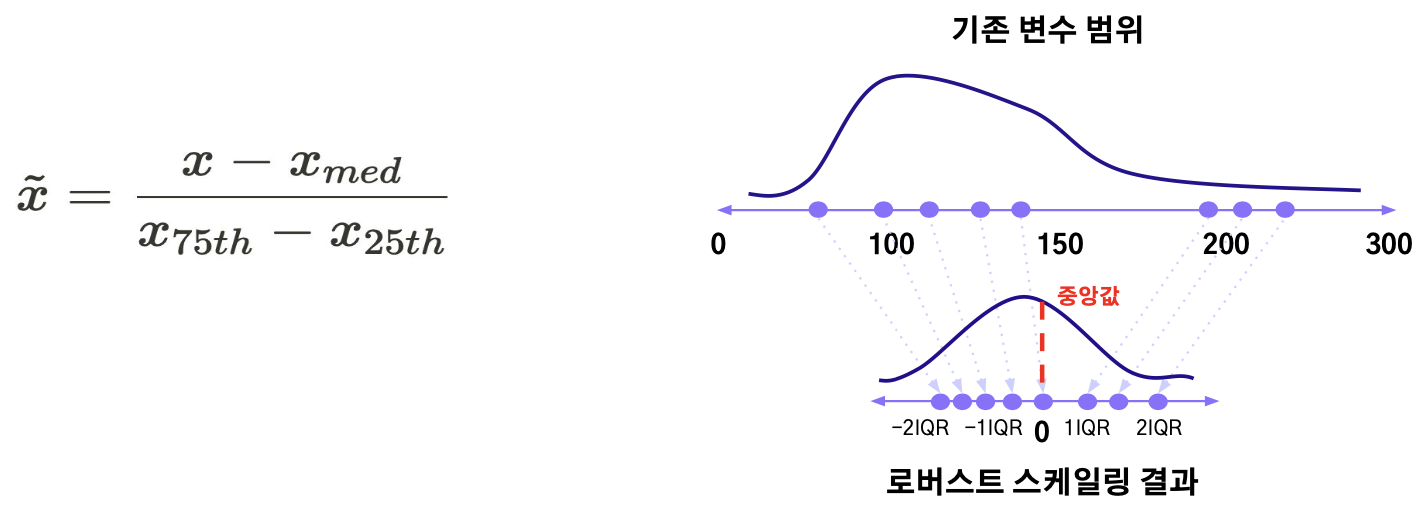
• 표준화와 다르게 평균 대신 중앙값을 활용하므로 이상치에 강건한 효과
• 표준화는 데이터에 이상치가 존재하면 평균이나 표준편차에 큰 영향

1.3 구간화(Binning, Bucketing)

• 수치형 변수를 범주형 변수로 전환시키는 방법
• 데이터가 범주화 되기 때문에 학습 모델의 복잡도가 줄어드는 장점
• 21, 22, 39, 35 ... → 10대, 20대, 30대
• 등간격(동일 길이), 등빈도(동일 개수)로 나누어 구간화를 진행
• 수치 값들이 기준에 따라 범주로 통일 되기 때문에 이상치를 완화
• 데이터의 ‘구분’이 가능해지기 때문에 데이터 및 모델해석에 용이

02 범주형 변수 다루기

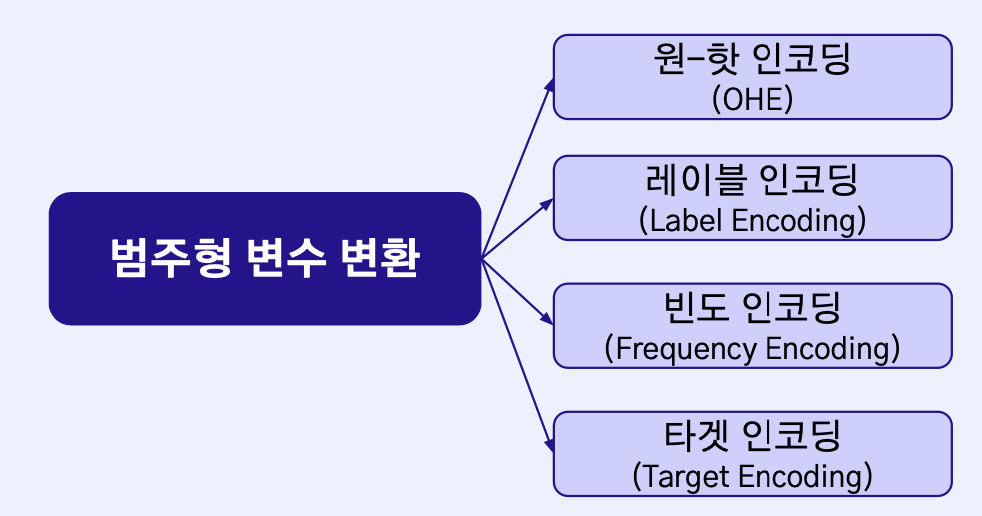
2.1 원-핫 인코딩

• 범주 변수를 0과 1로만 구성된 이진(binary) 벡터 형태로 변환하는 방법
• 고유 범주 변수 크기와 동일한 이진 벡터를 생성
• 범주에 해당하는 값만 1 설정, 나머지는 모두 0 변환

장점

• 변수의 이진화를 통해 컴퓨터가 인식하는 것에 적합
• 알고리즘 모델이 변수의 의미를 정확하게 파악 가능

단점

• 고유 범주 변수의 크기가 늘어날 때마다 희소 벡터 차원이 늘어나는 문제점이 존재
• 벡터의 차원이 늘어나면 메모리 및 연산에 악영향
• 차원의 저주 발생

2.2 레이블 인코딩

• 이진 벡터로 표현하는 원-핫 인코딩과 다르게 각 범주를 정수로 표현
• 하나의 변수(컬럼)으로 모든 범주 표현 가능
• 순서(Ordinal)가 존재하는 변수들에 적용할 경우 효율적

장점

• 범주 당 정수로 간단하게 변환 가능
• 하나의 변수로 표현 가능하기 때문에 메모리 관리 측면에서 효율적

단점

• 순서가 아닌 값을 순서로 인식할 수도 있는 문제가 발생

2.3 빈도 인코딩

• 고유 범주의 빈도 값을 인코딩
• 빈도가 높을수록 높은 정숫값을, 빈도가 낮을수록 낮은 정숫값을 부여 받는 형태
• 빈도 정보가 유지되어 학습에 적용시킬 수 있는 것이 특징
• Count Encoding이라고도 불림

장점

• 빈도라는 수치적인 의미를 변수에 부여 가능
• 하나의 변수(컬럼)로 표현 가능하기 때문에 메모리 관리 측면에서 효율적

단점

• 다른 특성의 의미를 지니고 있어도 빈도가 같으면, 다른 범주간 의미가 동일하게 인식될 가능성이 존재

2.4 타겟 인코딩

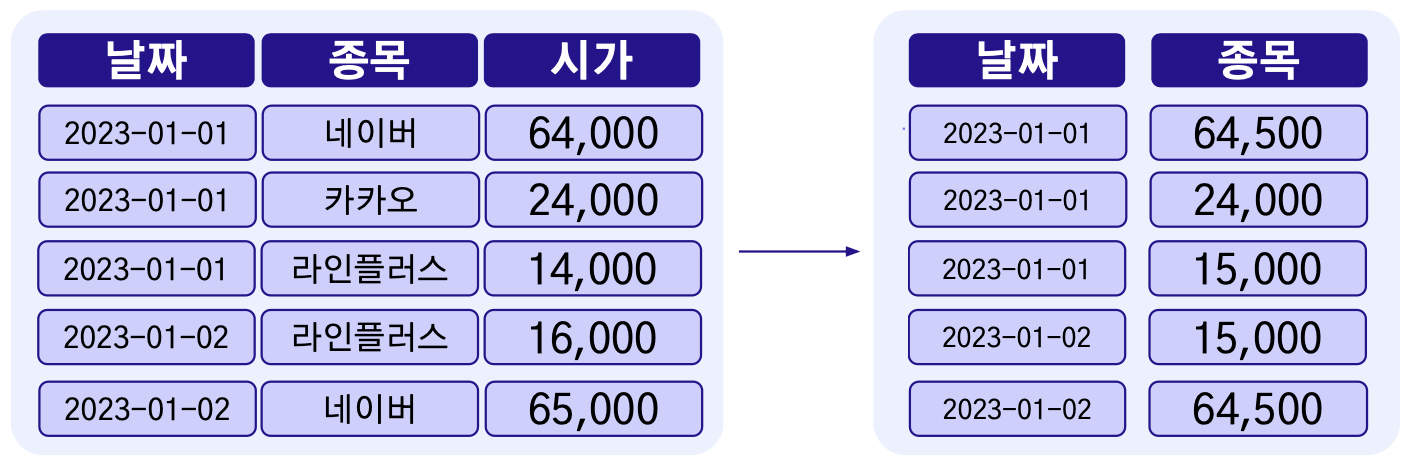
• 특정(타겟) 변수를 통계량(평균)으로 인코딩하는 방식
• 범주형 변수가 연속(Continuous)적인 특성을 가진 값으로 변환
• 범주형 변수가 특정 타겟 변수와 어떤 관련성이 있는지 파악하기 위한 목적도 존재
• Mean Encoding이라고도 불림

장점

• 범주 간 수치적인 의미를 변수에 부여 가능
• 타겟 변수라는 추가적인 정보를 가진 변수에 의존하므로 추가된 정보를 알고리즘에 입력 가능
• 하나의 변수로 표현 가능하기 때문에 메모리 관리 측면에서 효율적

단점

• 타겟 변수에 이상치가 존재하거나, 타겟 변수의 범주 종류가 소수라면 과적합 가능성이 존재
• 학습과 검증 데이터를 분할했을 때, 타겟 변수 특성이 학습 데이터셋에서 이미 노출되었기 때문에 Data-Leakage 발생

타겟 인코딩 과적합 방지

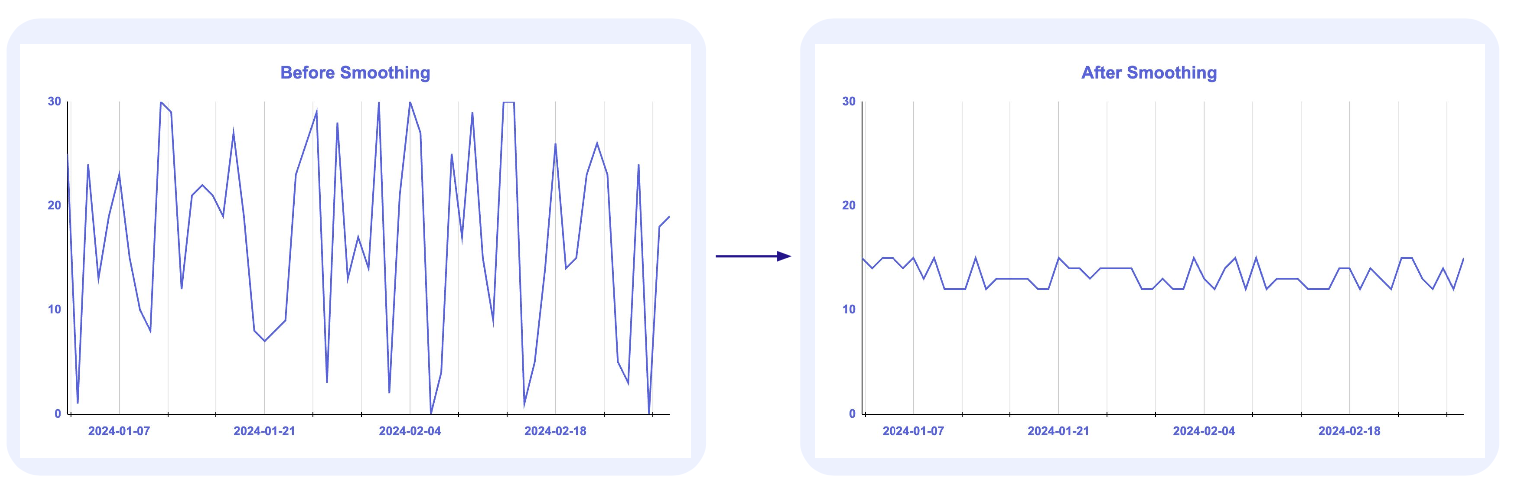
스무딩

• 전체(학습 + 검증) 데이터셋의 평균에 가깝게 전환
• 아래 그림처럼 기존 관측치를 전체 평균에 가까워지도록 규제를 가하는 방법 (데이터를 두드러지고 부드럽게 변화)

K-Fold

• 데이터 샘플(학습 데이터) 내에서도 다시 여러 데이터 샘플(Fold)로 재구성하여 각각 샘플을 타겟 인코딩을 하는 방식
• 타겟 인코딩 값이 보다 다양하게 생성