Missing Value
정의
- 데이터에서 누락(결측)된 관측치
- 데이터의 손실과 더불어, 분포를 왜곡시켜 편향을 야기시키는 원인
- N/A (Not Available) / NaN (Not a Number) / NULL / Empty / ? 등의 값으로 표현
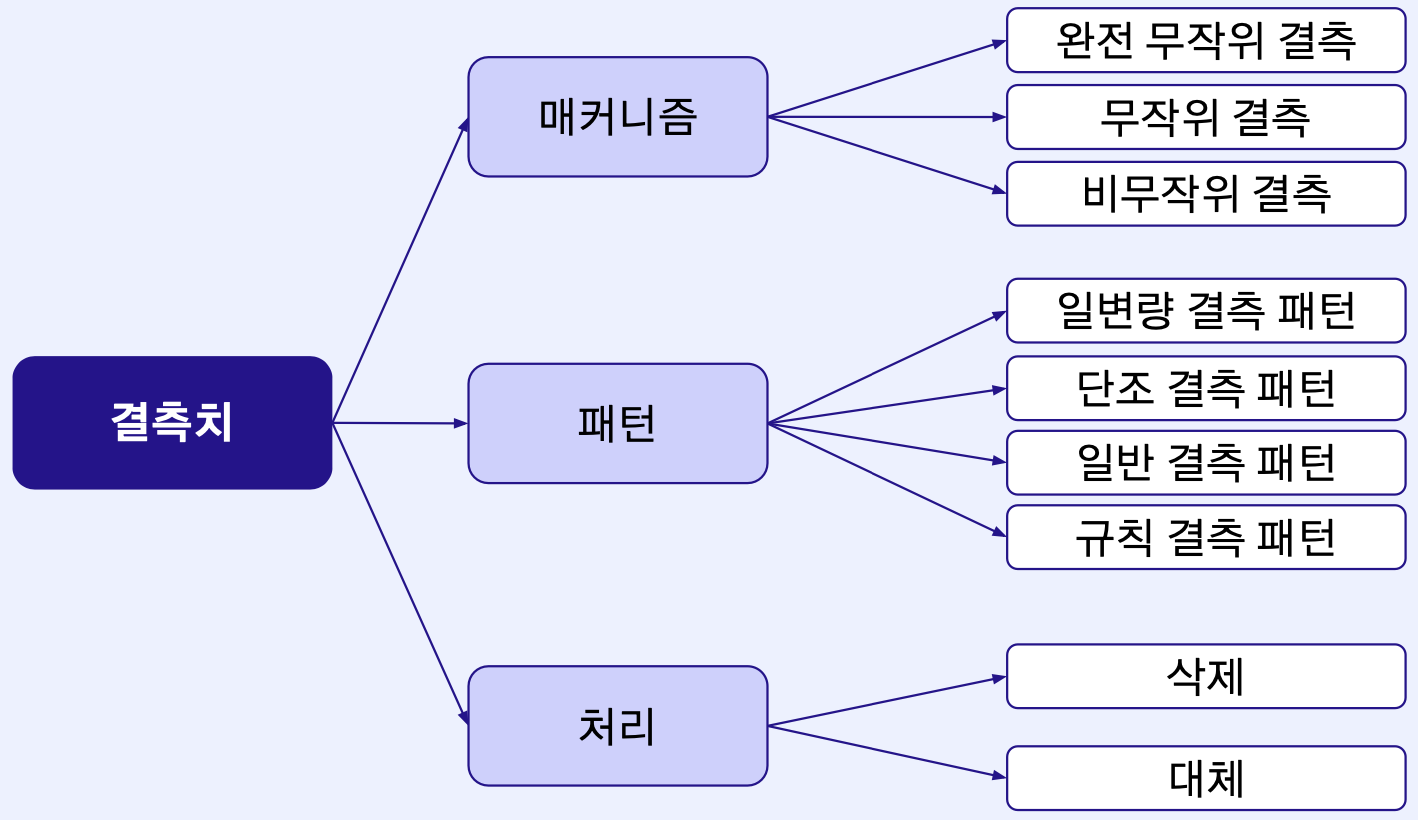
완전 무작위 결측 (MCAR)
- 결측치가 다른 변수와 상관 없이 무작위로 발생하는 경우
- 관측치와 결측치 모두 결측 원인과 독립
- 센서의 고장, 전산 오류 등의 이유로 발생 가능
무작위 결측(MAR)
- 결측치가 해당 변수와는 무관하나, 다른 변수와 연관되어 있는 경우
- 다른 변수의 관측치와 연관되어 있기 때문에 예측 모델을 통해 대체 가능 (다른 변수에 대한 의존 여부를 통해 검증 가능)
- 예) 설문조사에서 특정 키에 따라 몸무게에 대한 질문에 무응답인 경우 (몸무게와 키와의 연관)
비무작위 결측(MNAR)
- 결측의 원인이 해당 변수와 연관되어 발생
- MCAR, MCR에 해당되지 않는 결측 유형
- 예) 신체 정보 관련 설문조사에서 몸무게가 비교적 높은 응답군에서 결측이 많이 발생
일변량 결측 패턴(Univariate Pattern)
- 하나의 변수에서만 결측치가 발생
- 다른 변수와는 연관성이 없는 형태
- 예) 임상 실험 중 특정 하나의 집단에서만 부작용이 발생한 경우
단조 결측 패턴(Monotone Pattern)
- 일정하고 단조적인 패턴으로 결측치가 발생
- 임상 실험과 같은 종단(Longitudinal Study) 연구에서 많이 발생
- 예) 나이에 따른 사망, 악화 등 일정 개체에서 중도 탈락(Drop-Out)이 발생
일반 결측 패턴 (General & Non-Monotone Pattern)
- 단조적이지 않은 형태의 결측치
- 다른 변수와의 관계에 따라 나타날 수 있는 비선형 결측 패턴 형태
- 예) 알 수 없는 이유로 특정 나이에 따라 질병이 드물게 발생하는 경우
규칙 결측 패턴(Planned Pattern)
- 결측의 원인이 일정한 패턴 및 규칙에 따라 발생
- 특정 상황에 의해 의도적이며 규칙적으로 결측치를 생성하는 경우
Missing Value 처리
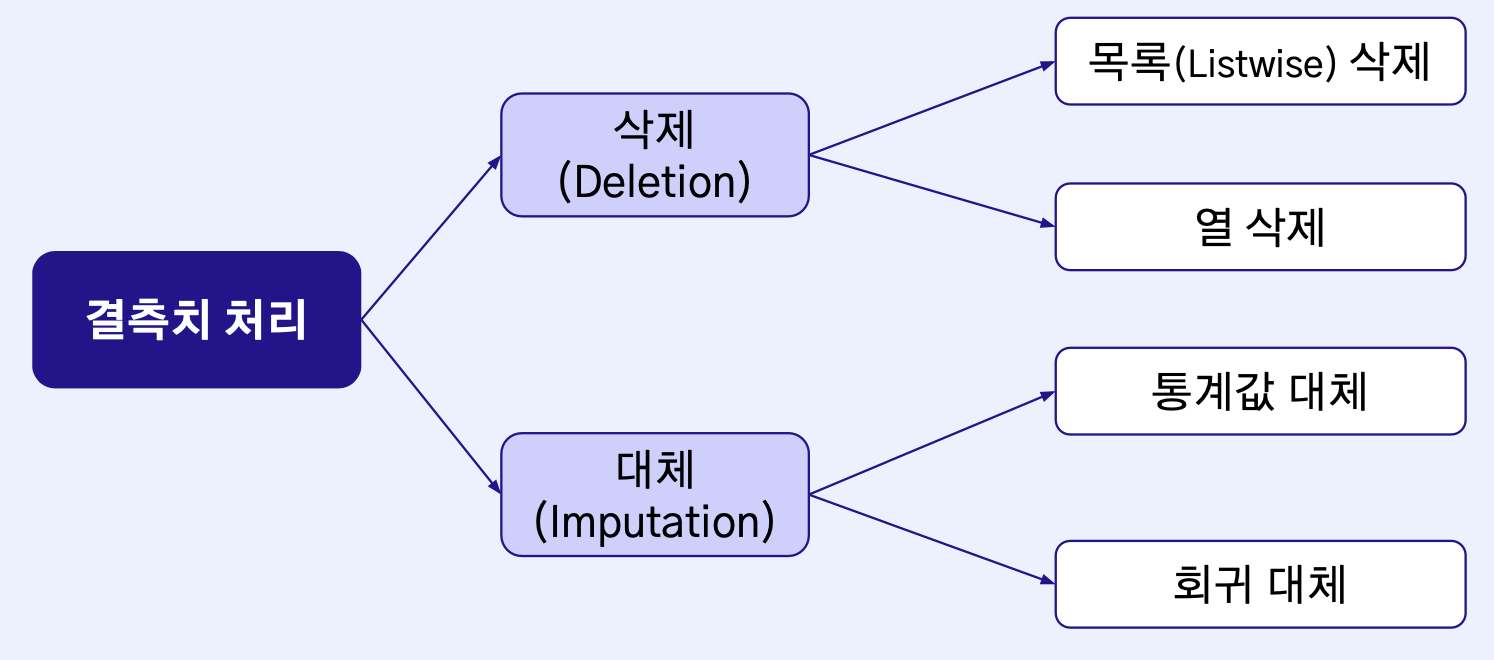
목록 삭제
- 변수에 결측치가 존재하는 해당 행을(Row) 제거
- 모든 변수가 결측치 없이 채워진 형태의 행만 분석 및 모델링에 활용하는 방식
열 삭제
변수에 결측치가 존재하는 해당 열을(Column) 제거
삭제 Pros & Cons
장점
- 결측치를 처리하기 편리
- 결측치가 데이터 왜곡의 원인이라면, 삭제로 인한 왜곡 방지와 알고리즘 모델 성능 향상 기대
단점
- 결측치에도 데이터 특성이 유효한 경우가 존재
- 삭제된 데이터로 인하여 남은 데이터에 편향이 만들어질 가능성
- 관측치의 정보가 줄어들게 되므로 알고리즘 모델에 악영향
대체(imputation)
결측치를 관측치의 통계값(평균값, 최빈값, 중앙값)으로 대체
장점
- 대체된 값은 데이터의 통계 특성을 반영하므로 정보를 안정적으로 보존 가능
- 데이터의 샘플이 그대로 유지되기 때문에 알고리즘 모델에 원본 크기로 적용 가능
단점
- 통계값으로 인해 변수의 분산이 감소하여 변수간 상관관계가 낮아지는 문제 발생
회귀 대체(regression imputation)
변수간의 관계를 파악 후, 예측하여 결측치를 대체하는 방식
장점
- 변수 간의 연관성을 활용해 결측치를 예측하기 때문에 많은 데이터 정보를 활용 가능
- 삭제(Deletion) 및 대체(Imputation) 방법에 비해 실제 데이터와의 유사 가능성이 높음
단점
- 예측 모델을 생성해야 하는 어려움
결측치 처리 방안
결측치 비율 ------ 결측치 처리 방법
10% 미만 ------ 제거(Deletion), 대체(Imputation)
10% ~ 20% ------ 회귀 대체 (Regression), Hot Deck
20% 이상 ------ 회귀 대체 (Regression)
물론 데이터 & 상황마다 변경될 수 있음.
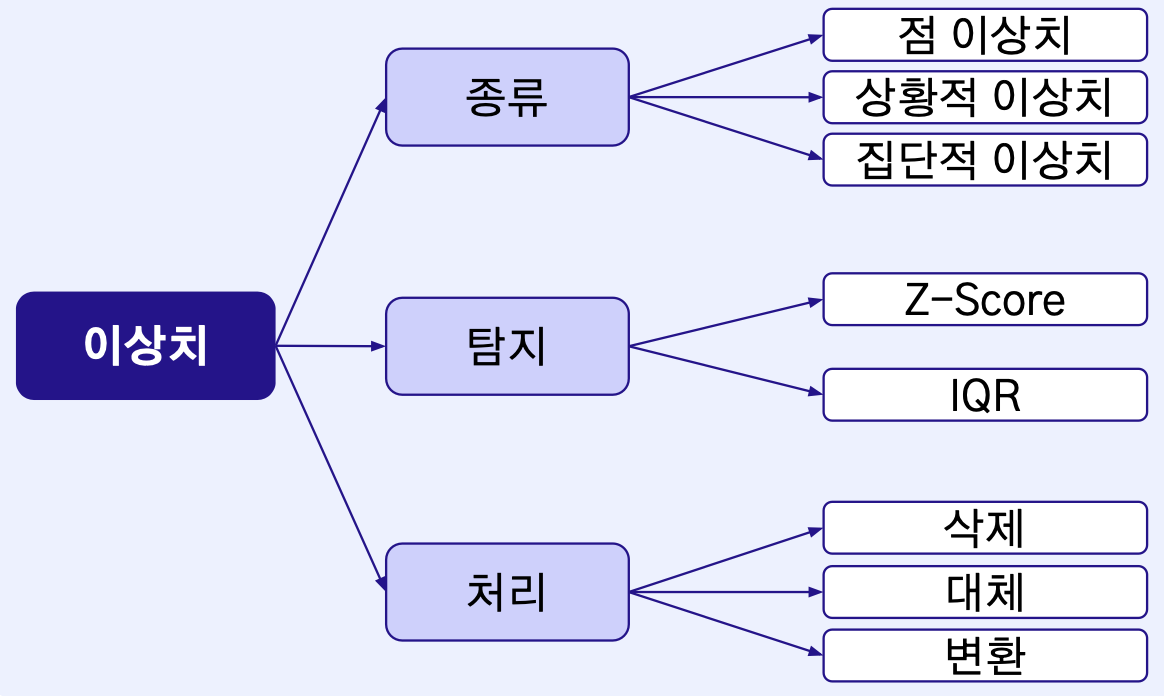
Outlier
정의
- 변수의 분포상 비정상적으로 극단적이며, 일반적인 데이터 패턴을 벗어나는 관측치
- 평균값과 같은 통계적 중요 결과를 왜곡 시키는 원인
- 예) 노스캐롤라이나 대학교 지리학과의 평균 초봉은 모든 과를 통틀어 가장 높은 수치를 한때 기록
이는 당시 슈퍼스타였던 마이클조던이 노스캐롤라이나 대학교 지리학과를 졸업했기 때문
왜 필요?
- 데이터 분석 및 탐색 시에 패턴과 인사이트를 도출하는 것이 가능
- 데이터로부터 도출된 명확한 패턴과 인사이트는 올바른 의사결정에 도움
- 데이터 전체를 왜곡시키는 이상치를 제거하여 모델의 안정성 향상을 기대
점 이상치(Point, Global Outlier)
- 대부분의 관측치들과 동떨어진 형태의 이상치
- 변수의 분포상 비정상적인 패턴을 가졌기 때문에 탐지가 어렵지 않은 케이스
상황적 이상치 (Contextual Outlier)
- 정상적인 데이터 패턴이라도 상황(Context)에 따라 이상치로 변환되는 형태
- 상황은 주로 시점에 따라 바뀌기 때문에 시계열 데이터에서 주로 나타나는 케이스
집단적 이상치 (Collective Outlier)
- 데이터 분포에서 집단적으로 편차가 이탈되어 이상치로 간주
- 관측치 개별로 보았을 때는 이상치처럼 보이지 않는 것이 특징
- 예) 스팸 메일은 일반 메일과 형태가 유사하지만, 정상적이지 못한 메일
Z-Score
- 평균으로부터의 표준편차 거리 단위를 측정하여 이상치를 탐지하는 방법
- Z 값을 측정하여 이상치를 탐색
- Z 값이 2.5~3정도 수치가 나오면 이상치로 판별
- 데이터가 정규분포를 따른다고 가정
장점
- 데이터에서 이상치를 간단하게 탐지 가능
단점
- 표준화된 점수를 도출하는 과정이기 때문에 데이터가 정규분포를 따르지 않는 경우 효과적이지 않을 가능성
- Z-Score를 구성하는 평균과 표준편차 자체가 이상치에 민감 (Modified Z-Score를 이용하는 방법도 존재)
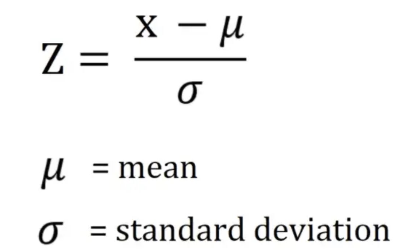
IQR (Inter Quartile Range)
- IQR은 상위 75%와 하위 25% 사이의 범위
- IQR은 Q3(제 3사분위)에서 Q1(제 1사분위)를 뺀 위치
- Q1 - 1.5 IQR 및 Q3 + 1.5 IQR 을 최극단의 이상치로 판단하여 처리
장점
- 데이터의 중앙값과 분포만을 통해 이상치를 식별하므로 직관적
- 표준편차 대신 백분위수(25%, 75%)를 사용하므로 이상치에 강건한 특징
- 데이터가 몰려 있는 경우라도 분포를 활용하기 때문에 효과적
단점 - 이상치의 식별 기준이 백분위수에 의존
- 왜도가 심하거나 정규분포를 따르지 않는 경우 제대로 작동하지 않을 가능성
이상치 처리 방식
- 결측치 처리와 마찬가지로 데이터를 삭제, 대체하는 방식으로 구분
- 변환(Transformation)을 통해서 단위(스케일)를 변환 시키는 방식도 존재
삭제(Deletion)
- 이상치에 해당하는 데이터 포인트(값, 인스턴스)를 제거하는 방법
- 다만, 이상치는 중요한 정보를 내포하고 있는 경우도 존재
- 이상치는 도메인 지식에 기반하여 객관적인 상황에 맞게 제거하는 것이 필요
대체(Imputation)
- 통계치(평균, 중앙, 최빈)으로 이상치를 대체
- 상한값(Upper boundary), 하한값(Lower boundary) 정해놓고 이상치가 경계를 넘어갈 때 대체
- 회귀 및 KNN 등의 거리기반 알고리즘 등을 이용해 이상치를 예측 및 대체하는 방식도 존재
변환(Transformation)
- 변수 내에서 매우 큰 값을 가진 이상치를 완화시킬 수 있는 방법 (큰 값을 작은 값으로 변환시키는 원리)
- 이외에도 제곱근 변환으로 대체하여 사용 가능
